
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РЕАКЦИИ ОПОРЫ
РЕАКЦИИ ОПОРЫ
Опорными называют реакции связей возникающие под действием внешних нагрузок в опорах и удерживающие рассматриваемый элемент или конструкцию в равновесии.
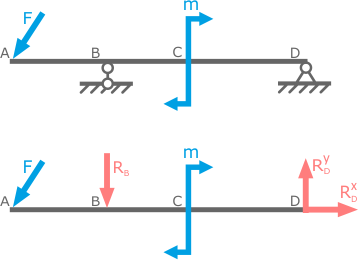
Замена опор их реакциями
При расчете элементов конструкций реакции опор также выступают в качестве внешних усилий приложенных к рассматриваемому телу.
Вопрос определения опорных реакций подробно рассматривается в курсе теоретической механики, но на практике часто применяется и при решении задач сопротивления материалов.
При этом некоторые задачи в сопромате можно решить без их определения. Это возможно в случаях, когда за расчетную схему принимается брус, закрепленный в жесткой опоре (заделке) без дополнительных опор, например, статически определимые консольные балки, стержни либо стержневые системы.
Определение реакций
Количество и направление реакций зависит как от вида опор, так и от способа нагружения бруса и для статически определимых систем определяются из уравнений равновесия конструкции или ее элементов.
Примеры расчета реакций опор
Для общего случая нагружения (пространственных систем), при котором может возникать до 6 реакций опор, требуется соответствующее количество уравнений.
Например, из условия, что заданная система относительно опор не перемещается в пространстве (вправо-влево, вверх-вниз, и вперед-назад) можем приравнять к нулю сумму проекций всех сил на оси x, y и z.
∑F(x)=0;
∑F(y)=0;
∑F(z)=0.
Из условия, что система не вращается, приравниваем к нулю суммы моментов всех нагрузок относительно соответствующих осей.
∑m(x)=0;
∑m(y)=0;
∑m(z)=0.
Совместное решение системы полученных уравнений позволяет определить величину и направление реакций в опорах.
Для плоской системы нагружения можно составить максимум три уравнения равновесия для определения до трех искомых усилий в опорах.
Линейно нагруженные элементы позволяют записать лишь одно уравнение равновесия.
Для расчета реакций опор статически неопределимых систем помимо уравнений статики требуются дополнительные зависимости, связывающие усилия с соответствующими им деформациями.
В некоторых случаях опорные реакции могут быть равны нулю. Это говорит лишь о том, что внешние нагрузки и остальные реакции взаимно уравновешены таким образом, что система может оставаться статичной и без соответствующего усилия в данной точке.
ВНЕШНИЕ СИЛЫ
Все внешние силы (нагрузки), действующие на изучаемое тело, следует рассматривать как проявление взаимодействия его с окружающими телами, которое представляется в виде сил или пар сил (моментов).
Все внешние силы (нагрузки) могут рассматриваться как сосредоточенные или распределённые.
В природе сосредоточенных сил не бывает. Все реальные тела практически контактируют через небольшие площадки. Однако принцип Сен-Венана позволяет распределенную нагрузку заменить равнодействующей силой, что упрощает расчёт.
Сосредоточенные нагрузки выражаются в ньютонах [H] и обозначается буквой F.
Распределённые нагрузки обозначаются буквой q и они бывают:
1. поверхностными (например, давление ветра, воды на стенку). Размерность [FL-2].
2. объёмными. Их размерность [FL-3].
3. распределенными по длине (например, силу тяжести стержня, учитывая небольшие размеры его поперечного сечения, рассматривают как распределённую нагрузку по длине). Размерность [FL-1].
Сосредоточенные и распределённые нагрузки могут быть как статическими, так и динамическими.
Статическими называются нагрузки, которые изменяют свою величину или точку приложения с очень небольшой скоростью, так что возникающими при этом ускорениями можно пренебречь.
Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. Возникшие при этом силы инерции могут многократно превосходить те же нагрузки, приложенные статически.
Законы изменения нагрузок во времени могут иметь весьма сложный характер.
В сопротивлении материалов основным изучаемым элементом конструкции является брус – тело, у которого один из линейных размеров (длина) значительно превышает два других, определяющих поперечное сечение. При работе конструкции ее элементы воспринимают внешние силы и действие их передают друг другу.
Классификация внешних нагрузок
Внешние силы делятся на активные и реактивные (реакции связей). Активные связи принято называть нагрузками.
По способу приложения нагрузки бывают объемные и поверхностные, распределенные и сосредоточенные, по характеру изменения в процессе приложения – статические, динамические и повторно-переменные, по продолжительности действия – постоянные и временные.
РАСЧЕТНАЯ СХЕМА РЕАЛЬНОЙ КОНСТРУКЦИИ
Реальные конструкции, как правило, характеризуются большой сложностью конструктивных форм (мост, купол и т.п.).
Провести расчёт реальных конструкции с учётом всех конструктивных особенностей очень часто сложно и иногда даже невозможно.
Вместе с тем конструктивные особенности не всегда оказывают существенное влияние на работу сооружения.
Поэтому при расчёте реальной конструкции её всегда заменяют идеализированной упрощённой схемой – так называемой расчётной схемой, выбор которой является исключительно ответственным этапом расчёта.
От этого выбора зависит точность и трудоёмкость расчёта. Иногда даже небольшое уточнение её ведёт за собой существенное усложнение расчёта или наоборот.
Расчётная схема должна полностью отражать основной характер работы реальной конструкции, устраняя несущественные второстепенные факторы.
При схематизации реальных объектов основными элементами расчётных схем являются: брус, оболочка, конструкция крепления этих элементов (опоры), также делаются упрощения в системе сил, приложенных к элементу конструкции.
ОСНОВНЫЕ ДЕФОРМАЦИИ
Под действием внешних нагрузок реальные тела и элементы деформируются, при этом точки или сечения элементов перемещаются относительно своего начального положения.
В сопротивлении материалов принято выделять четыре основных (простых) вида деформации:
1. Растяжение-сжатие;
2. Кручение;
3. Изгиб;
4. Сдвиг (срез).
Растяжение-сжатие
Растяжением-сжатием называют вид нагружения, при котором в поперечных сечениях бруса имеет место только внутренняя продольная сила N.
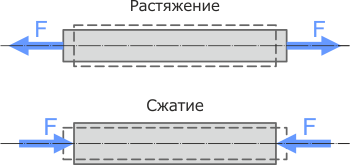
Деформацией при растяжении-сжатии является изменение длины стержня.
Кручение
Кручение – вид нагружения, при котором в поперечных сечениях бруса возникает только внутренний скручивающий момент T.
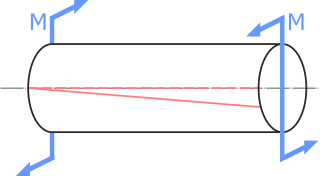
Деформация при кручении – поворот сечений вала относительно его продольной оси.
Изгиб
Изгибом называют деформацию, при которой происходит искривление продольной оси бруса.

В поперечных сечениях балки при этом появляется изгибающий момент M.
Сдвиг (срез)
Сдвигом называют случай, когда внешние усилия смещают параллельные сечения тела одно относительно другого с сохранением начального расстояния между ними.
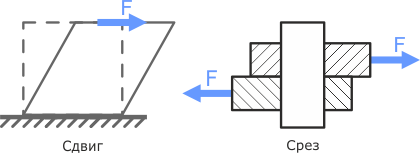
Деформация сдвига обусловлена наличием внутренних поперечных сил Q.
Срез является частным случаем сдвига, при котором сдвигаются смежные сечения.
Остальные деформации являются результатом совместного действия простых деформаций и рассматриваются в разделе «сложное сопротивление».
Классификация сил 
Силы делятся на внешние и внутренние. Внешние силы характеризуют взаимодействие между телами, внутренние – взаимодействие между частицами одного тела.
Внешние силы, действующие на элементы конструкций, делятся на активные, называемые нагрузкой, и реактивные (реакции связей). Нагрузка подразделяется на поверхностную и объемную. К поверхностной нагрузке относятся силы контакта, возникающие при сопряжении двух элементов конструкции или при их взаимодействии; к объемным (массовым) силам – силы, действующие на каждый бесконечно малый элемент объема. Примерами объемных сил являются силы инерции, силы тяжести, силы магнитного взаимодействия.
По характеру действия на конструкцию различают нагрузку:
- статическую – изменяется медленно и плавно от нуля до конечного значения так, что ускорения точек системы, возникающие при этом, весьма малы, поэтому силами инерции по сравнению с нагрузкой можно пренебречь;
- динамическую – прикладывается к телу за малый промежуток времени или мгновенно с образованием значительных ускорений;
- повторно-переменную – изменяющуюся по произвольному периодическому закону.
Внутренние силовые факторы (метод сечений)
Пусть свободное тело под действием системы сил 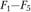 находится в равновесии (рис. 2.1). Требуется определить внутренние силы в сечении
находится в равновесии (рис. 2.1). Требуется определить внутренние силы в сечении 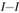 . Мысленно разрежем тело на две части по данному сечению и рассмотрим условия равновесия одной (любой) части тела. Обе части после разреза, вообще говоря, не будут находиться в равновесии, так как нарушены внутренние связи. Заменим действие левой части тела на правую и правой на левую некоторой системой сил в сечении
. Мысленно разрежем тело на две части по данному сечению и рассмотрим условия равновесия одной (любой) части тела. Обе части после разреза, вообще говоря, не будут находиться в равновесии, так как нарушены внутренние связи. Заменим действие левой части тела на правую и правой на левую некоторой системой сил в сечении 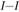 , т.е. внутренними силами (рис. 2.2). Характер распределения внутренних сил в сечении неизвестен, но они должны обеспечить равновесие каждой части тела. Для составления условия равновесия отсеченной части приведем внутренние силы в виде главного вектора и главного момента к центру тяжести сечения и спроецируем их на оси координат (рис. 2.3). Получим три проекции главного вектора
, т.е. внутренними силами (рис. 2.2). Характер распределения внутренних сил в сечении неизвестен, но они должны обеспечить равновесие каждой части тела. Для составления условия равновесия отсеченной части приведем внутренние силы в виде главного вектора и главного момента к центру тяжести сечения и спроецируем их на оси координат (рис. 2.3). Получим три проекции главного вектора 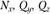 и три проекции главного момента
и три проекции главного момента 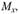
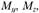 которые называются внутренними силовыми факторами:
которые называются внутренними силовыми факторами: 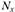 – продольная сила;
– продольная сила; 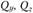 – поперечные силы;
– поперечные силы; 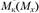 – крутящий момент;
– крутящий момент; 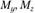 – изгибающие моменты.
– изгибающие моменты.
Составив условия равновесия отсеченной части, получим
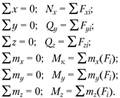 (2.1)
(2.1)
Уравнения (2.1) называются зависимостью между внешней нагрузкой на отсеченной части и внутренними силовыми факторами (статическими эквивалентами внутренних
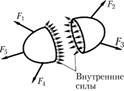
Рис. 2.1
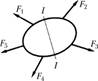
Рис. 2.2
сил). Если внешние нагрузки известны, то с их помощью можно определить внутренние силовые факторы.
Различают следующие основные виды деформаций:
- • растяжение-сжатие (рис. 2.4,а, б,
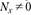 );
); - • сдвиг (рис. 2.4, в,
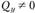 );
); - • кручение (рис. 2.4, г,
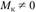 );
); - • изгиб (рис. 2.4, ∂,
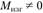 ).
).
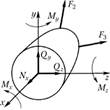
Рис. 2.3
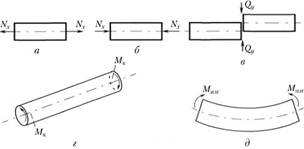
Рис. 2.4
Понятие о напряжении
Согласно гипотезе 1 (см. п. 2.1.1) можно предположить, что внутренние силы непрерывно распределены по площади поперечного сечения бруса. Пусть на малую, но конечную площадку А (рис. 2.5) действует внутренняя элементарная сила R. Разложив R на составляющие по осям 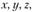 получим ее компоненты
получим ее компоненты 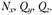 Отношение вида
Отношение вида
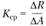 (2.2)
(2.2)
определяет среднее напряжение на данной площадке в данной точке.
Полное, или истинное, напряжение в точке есть отношение
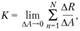 (2.3)
(2.3)
которое определяет интенсивность внутренних сил в данной точке рассматриваемого сечения. Поскольку через точку тела можно провести бесчисленное множество сечений, то в данной точке имеется бесчисленное множество напряжений, связанных с площадками действия. Совокупность всех напряжений, действующих на разных площадках в данной точке, называется напряженным состоянием точки. Единица напряжения – Н/м2 или Па. По аналогии с выражением (2.3) можно записать:
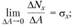 (2.4)
(2.4)
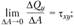 (2.5)
(2.5)
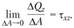 (2.6)
(2.6)
Выражение (2.4) определяет нормальное напряжение σx (рис. 2.6), вектор которого направлен так же, как и вектор нормальной силы Νx. Выражения (2.5) и (2.6) определяют касательные напряжения  ; их векторы имеют те же направления, что и, соответственно,
; их векторы имеют те же направления, что и, соответственно, 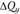 и
и 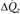 . Первый индекс при τ указывает, какой оси параллельна нормаль к площадке действия рассматриваемого напряжения, второй индекс показывает, какой оси параллельно данное напряжение.
. Первый индекс при τ указывает, какой оси параллельна нормаль к площадке действия рассматриваемого напряжения, второй индекс показывает, какой оси параллельно данное напряжение.
Зависимость между полным напряжением К и его составляющими выражается формулой
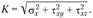 (2.7)
(2.7)
Рассмотрим связь между напряжениями и внутренними силовыми факторами в поперечном сечении бруса.
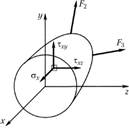
Рис. 2.5
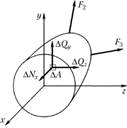
Рис. 2.6
Составляющие главного вектора и главного момента внутренних сил будут иметь следующий вид:
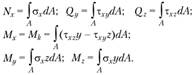
РЕАКЦИИ ОПОРЫ
Опорными называют реакции связей возникающие под действием внешних нагрузок в опорах и удерживающие рассматриваемый элемент или конструкцию в равновесии.

Замена опор их реакциями
При расчете элементов конструкций реакции опор также выступают в качестве внешних усилий приложенных к рассматриваемому телу.
Вопрос определения опорных реакций подробно рассматривается в курсе теоретической механики, но на практике часто применяется и при решении задач сопротивления материалов.
При этом некоторые задачи в сопромате можно решить без их определения. Это возможно в случаях, когда за расчетную схему принимается брус, закрепленный в жесткой опоре (заделке) без дополнительных опор, например, статически определимые консольные балки, стержни либо стержневые системы.
Определение реакций
Количество и направление реакций зависит как от вида опор, так и от способа нагружения бруса и для статически определимых систем определяются из уравнений равновесия конструкции или ее элементов.
Примеры расчета реакций опор >
Для общего случая нагружения (пространственных систем), при котором может возникать до 6 реакций опор, требуется соответствующее количество уравнений.
Например, из условия, что заданная система относительно опор не перемещается в пространстве (вправо-влево, вверх-вниз, и вперед-назад) можем приравнять к нулю сумму проекций всех сил на оси x, y и z.
∑F(x)=0;
∑F(y)=0;
∑F(z)=0.
Из условия, что система не вращается, приравниваем к нулю суммы моментов всех нагрузок относительно соответствующих осей.
∑m(x)=0;
∑m(y)=0;
∑m(z)=0.
Совместное решение системы полученных уравнений позволяет определить величину и направление реакций в опорах.
Для плоской системы нагружения можно составить максимум три уравнения равновесия для определения до трех искомых усилий в опорах.
Линейно нагруженные элементы позволяют записать лишь одно уравнение равновесия.
Для расчета реакций опор статически неопределимых систем помимо уравнений статики требуются дополнительные зависимости, связывающие усилия с соответствующими им деформациями.
В некоторых случаях опорные реакции могут быть равны нулю. Это говорит лишь о том, что внешние нагрузки и остальные реакции взаимно уравновешены таким образом, что система может оставаться статичной и без соответствующего усилия в данной точке.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|