Хелпикс

Главная

Контакты

Случайная статья



Группа 44 – дифференциальный зачет



Группа 44 – дифференциальный зачет

 

Айдакулов – 1 вариант (все задания под цифрой 1) - сдал

Зайцев – 2 вариант (все задания под цифрой 2)

Веселков – 3 вариант (все задания под цифрой 3)

Карпов – 4 вариант (все задания под цифрой 4)

Крылов - 5 вариант (все задания под цифрой 5)

Кузнецов– 6 вариант (все задания под цифрой 6)

Леликов– 7 вариант (все задания под цифрой 7)

Палкин – 8 вариант (все задания под цифрой 8)

Перевозников – 9 вариант (все задания под цифрой 9) - сдал

 

ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ

 дифференциального зачета

 

При выполнении дифференциального зачета по математике нужно придерживаться следующих правил:

 

1. Выполнить дифференциальный зачет на двойном листе , оставляя поля для ,

замечаний.

На первой странице написать

Дифференциальный зачет по математике

обучающегося ГАПОУ АО «АПТ» группы 44

ФИО

                   Дата

2. В работу включить все задачи, указанные в задании, строго по своему варианту.

3. Перед решением каждой задачи записать полностью ее условие.

4. Решения задач излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. 

ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ

 

1.Вычислите предел функции:

1.

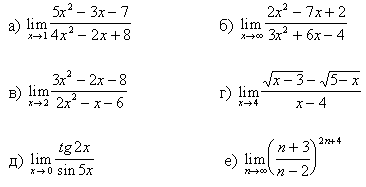
2.

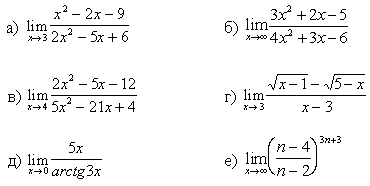
3.

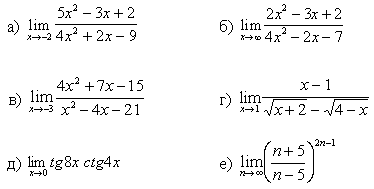
4.

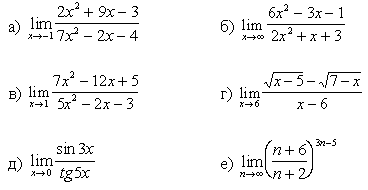
5.

6.

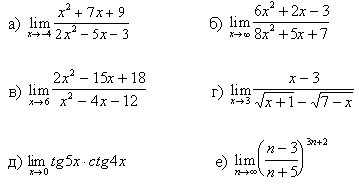
7.

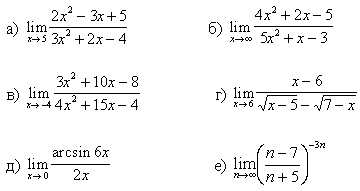
8.

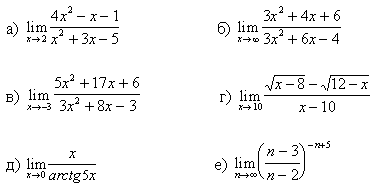
9.

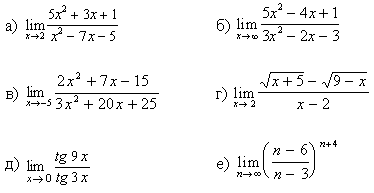
10.

 

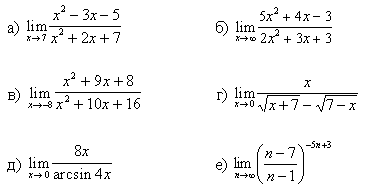
2. Произведите сложение (z1 + z2), вычитание(z1 - z2), умножение (z1 × z2) и

 деление(z1  z2)  комплексных чисел:

1. z1 = (3 + 5i)  и z2 = (2–7i)

2.  z1 = (6 + 2i) и z2=(5+3i)

3. z1 = (5 – 4i)  и   z2 = (6 + 2i)  

4. ) z1 = (2 + 3i) и  z2 = (5–7i)

5. ) z1 = (3+2i) и  z2 = (3–2i).

6. z1 = (7 6i) и z2 = (7+6i)

7. z1 = (4+i) и z2 = (4–5i).

8. z1 = 1–5i) и z2 = (3+5i).

9. z1 = (–2+3i) и  z2 = (3+5i).

10. z1 = (–3–5i) и z2 = (7–2i).

3. Найти интервалы выпуклости и вогнутости  функции

1. y = x5 - 80x2;

2. y = x3 - 3x2 + 1;

3. y = x4 - 2x3 + 6x - 4;

4. y = 6x3 + 2x;

5. y = 6x3 - 2x;

6. y = 4x4 - 4x3;

7. y = x3 + 3x2 + 1;

8. y = x5 + 80x2

9. y = 4x4 + 4x3;

10. y = x3 + 6x2

 

4.Исследуйте средствами дифференциального исчисления функцию y = f(x) и построите ее график.

1. y = x3 - 9x2 + 24x - 16

2. y = x3 -11x2 + 39x - 45

3. y = x3 + 6x2 + 9x + 4

4. y = x3 + x2 - 5x + 3

5. y = x3 + 10x2 +32x + 32

6. y = x3 + 9x2 + 24x + 20

7. y = x3 - 14x2 + 60x - 72

8. y = x3 - 12x2 + 45x - 54

9. y = x3 - 18x2 + 105x -196

10. y = x3 - 10x2 + 28x – 24

 

5. Вычислите интеграл

1.

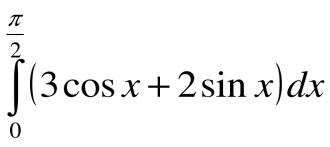
2.

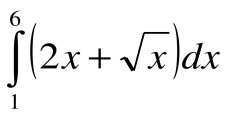
3.

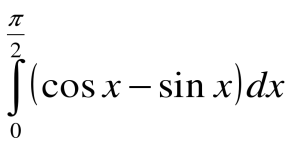
4.

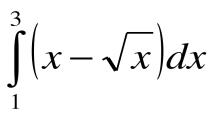
5.

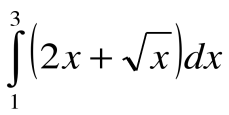
6.

 

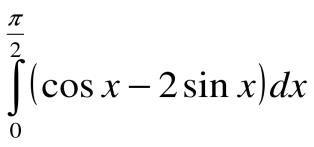
7.

 

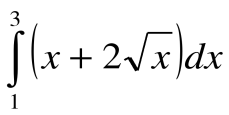
8.

 

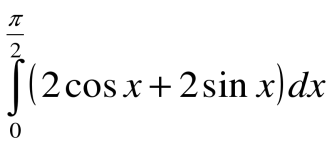
9.

 

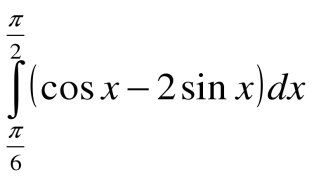
10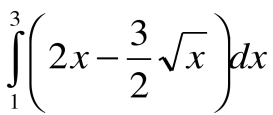

 

6.Вычислите площадь фигуры, ограниченной параболой у = ах2 + bх + с и прямой у = kх + b. Сделайте чертеж.

1. у = -х2 + 4х - 1; у = -х - 1.

2. у = х2 - 6х + 7; у = х + 1

3. у = -х2 + 6х -5; у = х - 5

4. у = х2 - 6х + 7; у = -х + 7

5. у = -х2 + 6х - 5; у = -х + 1

6. у = х2 + 6х + 7; у = х + 7

7. у = -х2 - 6х - 5; у = х + 1

8. у = х2 + 6х + 7; у = -х + 1

9. у = -х2 - 6х - 6; у = -х - 6

10. у = х2 - 4х + 1; у = х + 1

7. Решить систему линейных уравнений методом Крамера и методом Гаусса.

1.

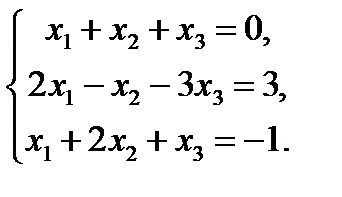
2.

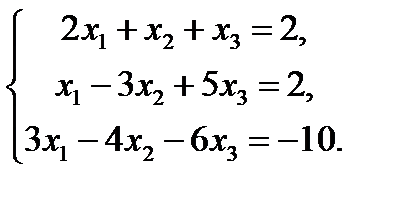
3.

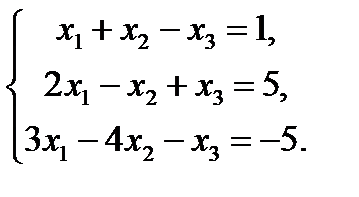
4.

5.

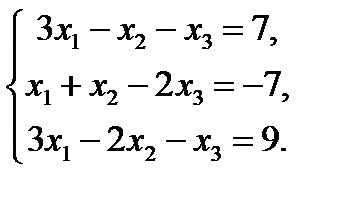
6.

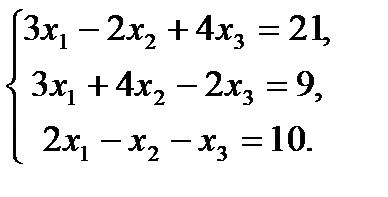
7.

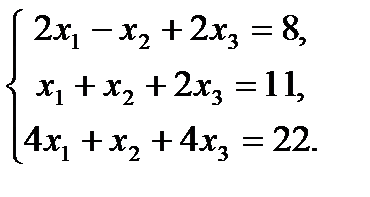
8.

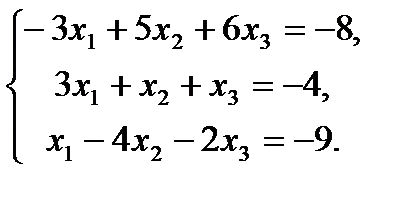
9.

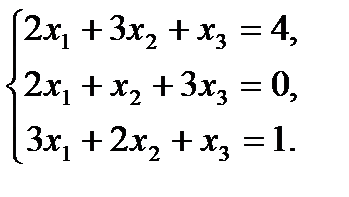
10.

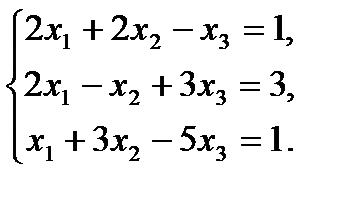
Критерии оценивания

4заданий – «3»

5заданий – «4»

6заданий – «5»

 

 

 


  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.