Тема: «Потенциал и разность потенциалов»

Тема: «Потенциал и разность потенциалов»

Темой сегодняшнего урока будет ещё одна характеристика электрического поля – энергетическая. Эта характеристика называется потенциалом, и она непосредственно связана с работой электрического поля по перемещению заряда. Но для начала вспомним другую характеристику поля – силовую характеристику, напряженность:

для произвольного поля в некоторой точке пространства напряженность равна:

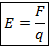
а для поля точечного заряда:

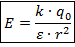
Теперь вспомним из курса механики, как вычислить работу, совершаемую над телом – в нашем случае электрическое поле совершает работу по перемещению заряда:

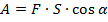
учитывая:

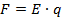
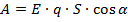
· Теперь пришло время ввести новую энергетическую характеристику поля – потенциал.

Потенциал –физическая величина, показывающая отношение потенциальной энергии заряда в некоторой точке пространства к величине этого заряда:

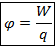
Так как потенциальная энергия заряда прямо пропорциональна величине заряда, то потенциал от величины заряда не зависит:

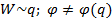
Единица измерения потенциала – вольт:

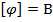
Потенциал некоторой точки пространства можно определить как работу электрического поля по переносу единичного заряда из бесконечности в эту точку. В общем же виде связь потенциала с работой можно задать через ввод электрического напряжения:

Полученная зависимость справедлива вдоль некоторой силовой линии, и здесь 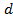– расстояние между двумя точками на одной силовой линии.

Зависимость потенциала поля точечного заряда от расстояния имеет похожий вид с аналогичной зависимостью для напряженности, однако убывает медленнее – не пропорционально квадрату, а пропорционально первой степени:

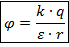
· Эквипотенциальные поверхности

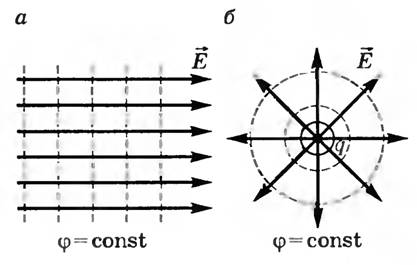
Нам уже известно, что графически напряженность изображается в виде силовых линий, направленных от положительных зарядов к отрицательным. Потенциалы можно также графически отобразить в виде эквипотенциальных поверхностей.

Эквипотенциальная поверхность – поверхность, каждая точка которой имеет одинаковый потенциал.

Как следует из связи работы и потенциалов:

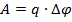
при переносе заряда вдоль эквипотенциальных поверхностей электрическое поле работы не совершает, так как .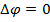

Работа при ненулевой силе равна нулю только в том случае, если вектор силы перпендикулярен вектору перемещения. Из этого следует, что линии напряженности перпендикулярны эквипотенциальным поверхностям. Примерами эквипотенциальных поверхностей служат сферы для поля точечного заряда и параллельные плоскости для однородных полей (рис. 3).

12 Следующая ⇒