
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА»
(РУТ (МИИТ)
Факультет "Транспортные сооружения и здания"
Кафедра "Здания и сооружения на транспорте"
Курсовая работа
по дисциплине
«Механика грунтов»
| Проверил: __________________ Подпись | Выполнил: студент 3-го курса Ганичкин В. В. Шифр: 1710-ц/СЖс-2221 |
Москва 2020
Содержание
I часть
1. Определение природных напряжений в массиве грунта................................3
2. Определение напряжений в массиве грунта от действия на его поверхности внешней прямоугольной нагрузки методом угловых точек..............................6
3. Расчет осадки слоя грунта под действием сплошной равномерно распределенной нагрузки.....................................................................................11
4. Оценка устойчивости однородного откоса.....................................................13
5. Определение давления грунта на подпорную стену......................................21
6. Определение давления грунта на подземный трубопровод..........................26
II часть
Оценка строительных свойств грунтов строительной площадки и определение размеров фундамента.....................................................................33
Список используемой литературы......................................................................43
Часть 1
Задача №1 вариант №5
Определение напряжений от собственного веса грунта
(природного или бытового давления).
Исходные данные:
Грунт №1: тип грунта – песок пылеватый; толщина слоя 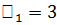 м;
м;
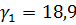 кН/м3;
кН/м3; 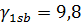 кН/м3; глубина уровня грунтовых вод
кН/м3; глубина уровня грунтовых вод 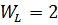 м.
м.
Грунт №2: тип водоупора – глина; расчётная глубина определения 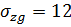 м;
м; 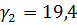 кН/м3; коэффициент Пуассона для глины
кН/м3; коэффициент Пуассона для глины 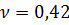 .
.
Напряжение от собственного веса грунта имеют значения для свеженасыпанных земляных сооружений, оценки природной уплотнённости грунтов и в расчётах осадок оснований фундаментов. При горизонтальной поверхности грунта напряжений от собственного веса будут увеличиваться с глубиной.
Вертикальное напряжение от собственного веса грунта 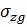 представляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице.
представляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице.
При постоянном удельном весе грунта 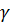 по глубине по оси
по глубине по оси 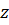 напряжения
напряжения 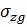 определяются по формуле:
определяются по формуле:
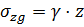 .
.
При слоистом залегании грунтов обладающих различным удельным весом или наличии грунтовых вод величина 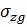 определяется суммированием (Рисунок 1.1):
определяется суммированием (Рисунок 1.1):
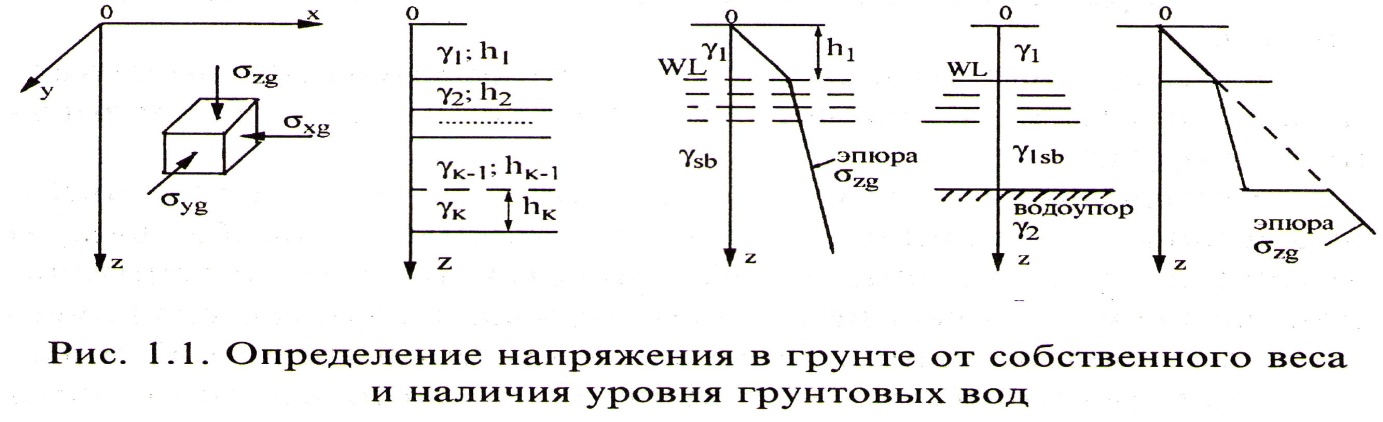

Горизонтальное напряжение 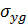 и
и 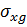 также увеличиваются с глубиной и определяются по формуле:
также увеличиваются с глубиной и определяются по формуле:
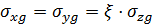 , где:
, где:
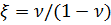 - коэффициент бокового давления грунта;
- коэффициент бокового давления грунта; 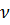 - коэффициент относительных поперечных деформаций, аналогично коэффициенту Пуассона упругих тел.
- коэффициент относительных поперечных деформаций, аналогично коэффициенту Пуассона упругих тел.
Решение:
Требуется определить напряжения от собственного веса грунта на глубине 12 м от поверхности. Основание до глубины 3 м сложено песком пылеватым с плотностью 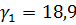 кН/м3;
кН/м3; 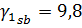 кН/м3. Песок подстилается слоем глины
кН/м3. Песок подстилается слоем глины 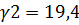 кН/м3 являющейся водоупором. Уровень грунтовых вод
кН/м3 являющейся водоупором. Уровень грунтовых вод 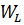 расположен в супеси на глубине 2 м от поверхности.
расположен в супеси на глубине 2 м от поверхности.
В точке 1 на глубине 2 м: 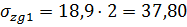 кПа;
кПа;
В точке 2 на глубине 3 м: 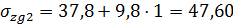 кПа;
кПа;
В точке 2’на глубине 3 м: 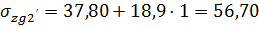 кПа;
кПа;
В точке 3 на глубине 12 м: 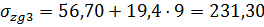 кПа;
кПа;
В точке 3 на глубине 12 м: 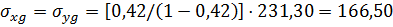 кПа.
кПа.
Эпюра напряжений 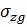 от собственного веса грунта представлена на миллиметровой бумаге.
от собственного веса грунта представлена на миллиметровой бумаге.
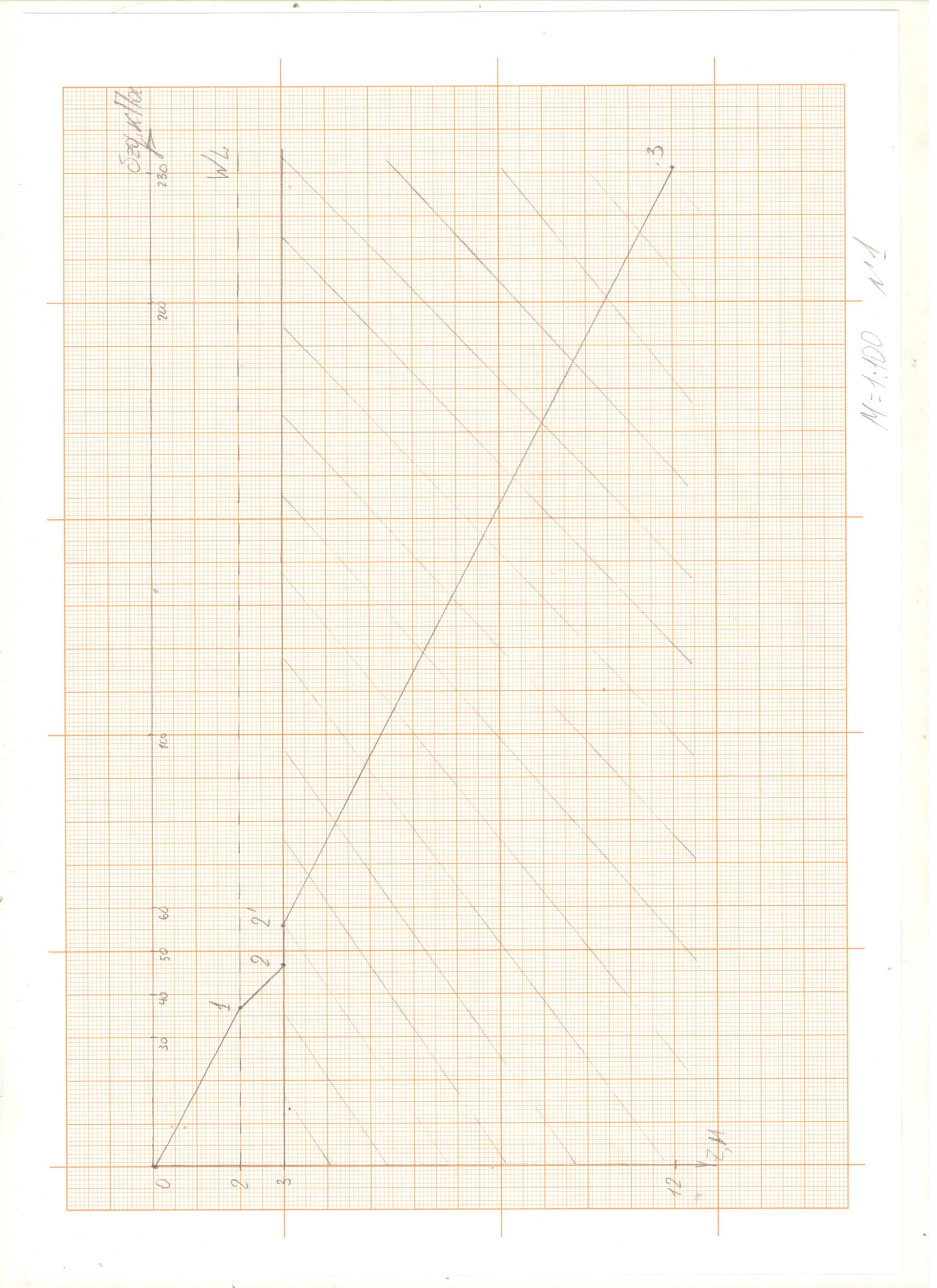
Задача №2 вариант №6
Определение напряжений в грунтовом основании от действия прямоугольной нагрузки приложенной на его поверхности.
Исходные данные:
Размеры загруженного прямоугольника: b=3м; l=5м; внешняя нагрузка интенсивностью р=0,42МПа =4.2 кгс/см2.
Определение напряжений в грунтовой толще от действия внешних нагрузок необходимо для установления условий прочности и устойчивости грунтов, определения деформаций и осадок оснований фундаментов. При решении вопроса о распределении напряжений в грунтах применяют теорию линейно деформируемых тел. Для определения напряжений по этой теории будут полностью справедливы уравнения теории упругости, также базирующиеся на линейной зависимости между напряжениями и деформациями (закон Гука). Определение сжимающих напряжений от действия прямоугольной нагрузки в произвольной точке основания производится на основе метода угловатых точек. Значение величин сжимающих напряжений для угловатых точек прямоугольной площади загрузки позволяет очень быстро вычислить сжимающие напряжения для любой точки полупространства (грунтового основания) если пользоваться значениями угловых коэффициентов 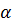 и
и 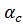 .
.
Для точек расположенных по вертикальной оси под центром загруженного прямоугольника сжимающие напряжения:
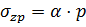
А для точек расположенных по вертикальной оси под углом загруженного прямоугольника:
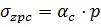 , где:
, где:
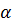 - коэффициент, принимаемый по таблице в зависимости от соотношения сторон
- коэффициент, принимаемый по таблице в зависимости от соотношения сторон 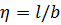 прямоугольной нагрузки (формы подошвы фундамента) и относительной глубины, равной:
прямоугольной нагрузки (формы подошвы фундамента) и относительной глубины, равной: 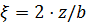 - при определении
- при определении 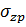 ;
; 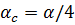 - коэффициент, при определении
- коэффициент, при определении 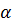 в данном случае по таблице
в данном случае по таблице 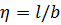 , а относительная глубина
, а относительная глубина 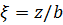 .
.
Характерный вид эпюры 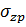 показан на рисунке 2.1.
показан на рисунке 2.1.
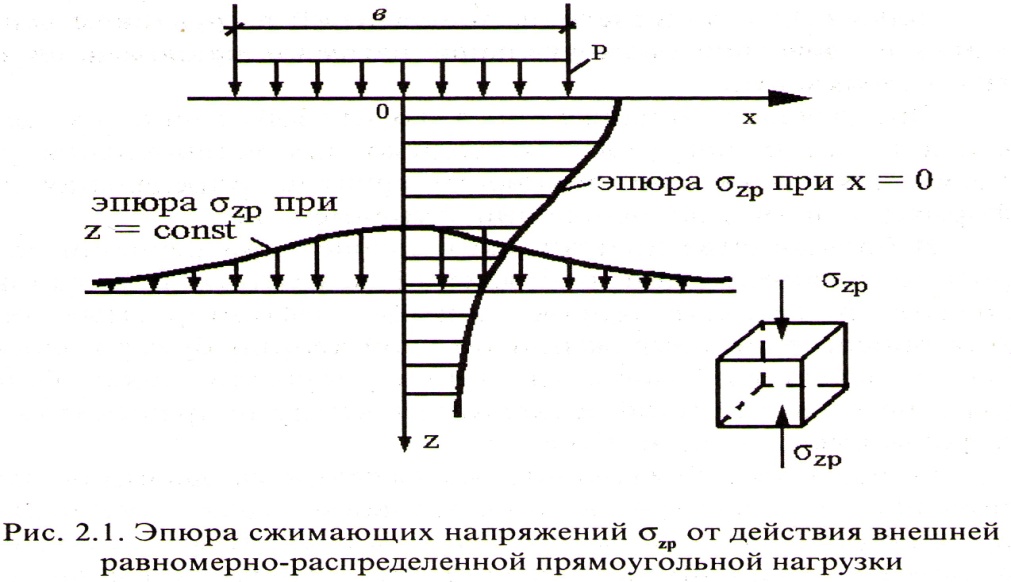
Метод угловатых точек для определения сжимающих напряжений 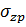 принимают в случае, когда грузовая площадь может быть разбита на такие прямоугольники, чтобы рассматриваемая точка оказалась угловой. Тогда сжимающее напряжение в этой точке на любой глубине будет равно алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой.
принимают в случае, когда грузовая площадь может быть разбита на такие прямоугольники, чтобы рассматриваемая точка оказалась угловой. Тогда сжимающее напряжение в этой точке на любой глубине будет равно алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой.
Рассмотрим три основных случая:
1) точка М находится на контуре прямоугольника внешних воздействий (Рисунок 2.2, а);
2) точка М находится внутри прямоугольника давлений (Рисунок 2.2, б);
3) точка М находится вне прямоугольника давлений (Рисунок 2.2, в).
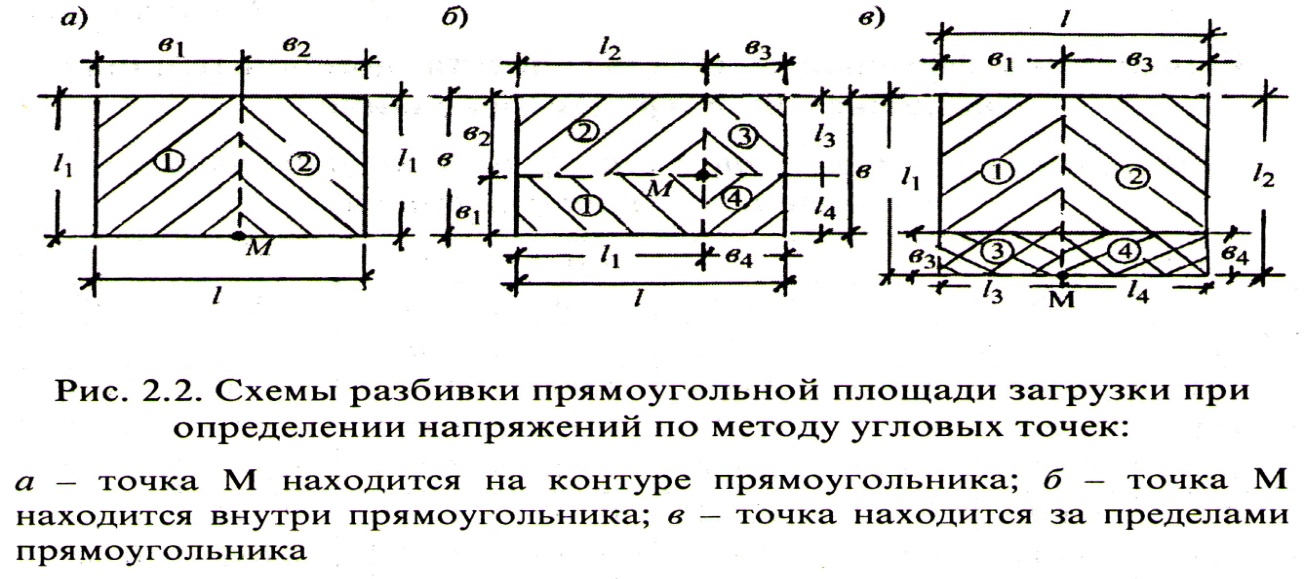
В первом случае величина 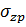 на заданной глубине
на заданной глубине 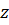 под точкой М определяется как сумма двух угловых напряжений, соответствующих прямоугольников 1 и 2, то есть:
под точкой М определяется как сумма двух угловых напряжений, соответствующих прямоугольников 1 и 2, то есть:
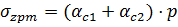
Во втором случае необходимо суммировать угловатые напряжения от четырёх прямоугольных площадей загрузки 1,2,3,4:
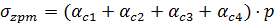
В третьем случае напряжение в точке М складывается из суммы напряжений от действия нагрузки по прямоугольникам 1 и 2, взятых со знаком «плюс», и напряжений от действия нагрузки по прямоугольникам 3 и 4, взятых со знаком «минус».
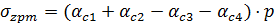
Решение:
Определить сжимающие напряжения под центром и под серединой длинной стороны загружаемого прямоугольника размером в плане 5×3м на глубине z=0 м; z=0,5b; z=1,0b; z=2,0b от поверхности при внешней нагрузке интенсивностью p=0,42МПа = 4.2 кгс/см2 .
Под центром загруженной площади η=l/b=5/3=1.67; 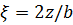 ;
; 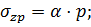
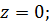
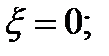

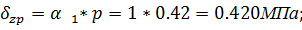
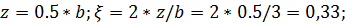
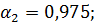
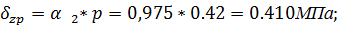
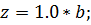
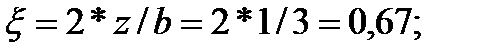
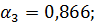
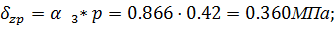
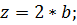
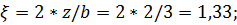
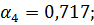
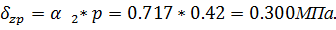
Значения 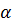 определяются по таблице в зависимости от параметров
определяются по таблице в зависимости от параметров 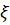 и
и 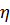 . Для промежуточных значений интерполяцией.
. Для промежуточных значений интерполяцией.
Для точки под серединой длинной стороны прямоугольника площади загрузки, разделяем её на два прямоугольника размером 2.5*3 м так, чтобы рассматриваемая точка была бы угловой.
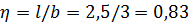
Значения 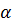 определяются по таблице в зависимости от параметров
определяются по таблице в зависимости от параметров 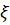 и
и 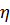 . Для промежуточных значений интерполяцией.
. Для промежуточных значений интерполяцией.
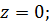
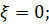

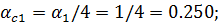
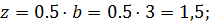
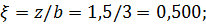
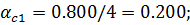
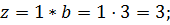
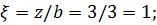
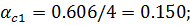
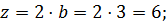
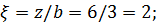
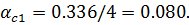
Так как прямоугольники 1 и 2 имеют одинаковые размеры: 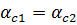 , тогда
, тогда 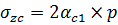
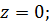
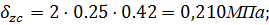
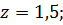
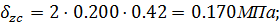
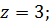
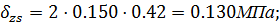
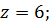
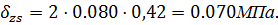
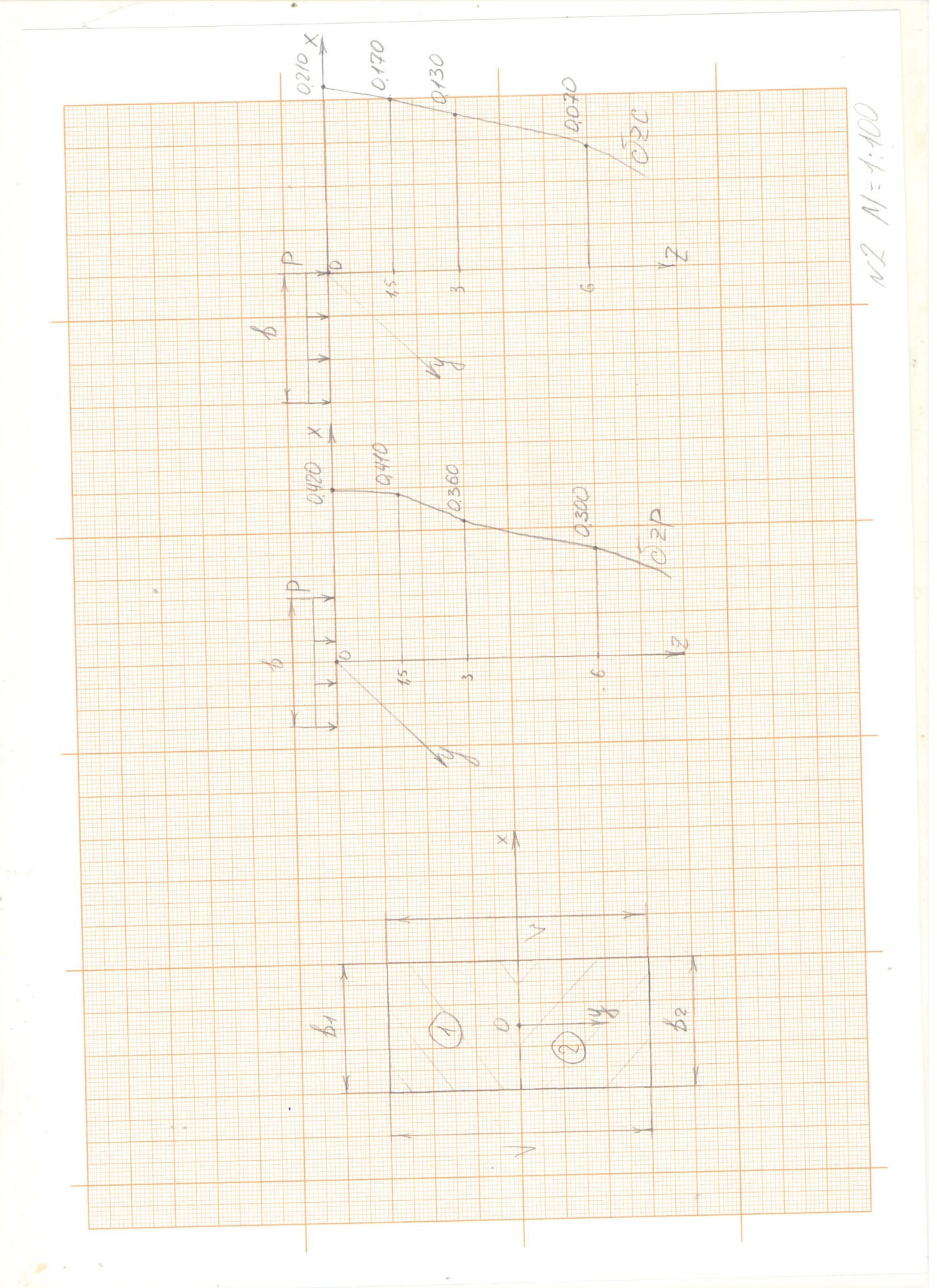
Эпюра сжимающих напряжений методом угловатых точек 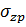 и
и 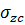 представлена на миллиметровой бумаге.
представлена на миллиметровой бумаге.
Задача №3 вариант №5
Расчёт осадки слоя грунта под действием сплошной равномерно-распределённой нагрузки (одномерная задача теории компрессионного уплотнения грунтов).
Исходные данные:
Высота слоя грунта: h=3,8 м; коэффициент Пуассона грунта: 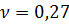 ;
;
коэффициент относительной сжимаемости грунта: 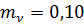 МПа-1;
МПа-1;
сплошная равномерно-распределённая нагрузка: P=0,35 МПа.
При действии сплошной нагрузки (распределённой на значительные расстояния в стороны) слой грунта будет испытывать только сжатие без возможности бокового расширения. Данные условия совершенно аналогичны компрессионному сжатию в цилиндре с жёсткими стенками (в лабораторных условиях при испытании грунта на сжатие в одометре - компрессионном приборе). В рассматриваемых условиях будем иметь строго одномерную задачу компрессионного уплотнения (грунт деформируется только в направлении одной оси).
Учитывая, что при относительно небольшом изменении давления, изменение коэффициента пористости прямо пропорционально изменению давления, полная стабилизационная осадка грунта будет равна:
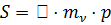 , где:
, где:
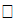 - высота слоя грунта в м;
- высота слоя грунта в м; 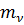 - коэффициент относительной сжимаемости грунта, МПа-1.
- коэффициент относительной сжимаемости грунта, МПа-1.
Так как 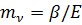 , то:
, то:
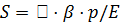 , где:
, где:
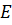 - модуль деформации грунта, МПа;
- модуль деформации грунта, МПа;
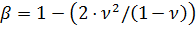
Определяем модуль деформации грунта по формуле:
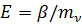
Решение:Определить стабилизированную осадку слоя грунта высотой 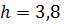 м, под действием сплошной равномерно-распределённой нагрузки
м, под действием сплошной равномерно-распределённой нагрузки 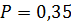 МПа. Грунт характеризуется коэффициентом относительной сжимаемости
МПа. Грунт характеризуется коэффициентом относительной сжимаемости 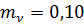 МПа-1 и коэффициентом Пуассона грунта
МПа-1 и коэффициентом Пуассона грунта 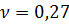 .
.
Определяем параметры 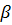 ,
, 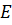 и
и 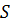 :
:
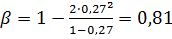 ;
; 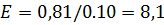 МПа;
МПа;
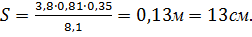
Схема сжатия грунта при сплошной нагрузке представлена на миллиметровой бумаге.
Задача №4 вариант № 5
Оценка степени устойчивости откоса методом круглоцилиндрических поверхностей скольжения (КЦПС)
Исходные данные:
Высота склона:  =12 м; склон сложен суглинком с параметрами:
=12 м; склон сложен суглинком с параметрами:
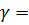 20 кН/м3;
20 кН/м3; 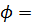 110;
110; 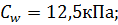 крутизна склона характеризуется углом наклона линии склона к горизонту
крутизна склона характеризуется углом наклона линии склона к горизонту 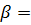 450.
450.
Анализ устойчивости массивов грунта имеет большое практическое значение при проектировании земляных сооружений: насыпей, выемок, дамб; при оценке устойчивости естественных склонов.
Устойчивость откосов зависит от:
- прочности грунтов, слагающий откос и в его основании (параметров сопротивления грунтов сдвигу 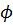 ;
; 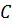 );
);
- крутизны откоса;
- высоты откоса;
- нагрузок на поверхности откоса;
- фильтраций воды через откос.
Главнейшие причины нарушения устойчивости земляных масс: 1 - эрозионные процессы; 2 - нарушение равновесия. Эрозионные процессы протекают весьма медленно и обычно не рассматриваются в механике грунтов. Нарушение равновесия массивов грунта может происходить внезапно, со сползанием значительных масс грунта – такие нарушения равновесия называются оползнями. Этот вид нарушений равновесия является наиболее частым.
Возможными причинами нарушения устойчивости откосов являются:
- излишняя его крутизна;
- подрезка откоса в нижней части;
- утяжеление откоса вследствие увлажнения грунта;
- уменьшение параметров сопротивления сдвигу грунта тела откоса вследствие увлажнения, промерзания и оттаивания и других факторов;
- нагрузка на гребень откоса;
- динамическое воздействие.
Метод круглоцилиндрических поверхностей скольжения широко применяется на практике для оценки устойчивости откосов насыпей и естественных склонов и является наиболее распространенным из методов расчёта. Метод основывается на опытных данных о форме поверхностей скольжения при оползнях вращения, при этом самое невыгодное их положение определяется расчётом. Задача расчёта заключается в определении коэффициента устойчивости природного склона или откоса насыпи для наиболее опасной поверхности скольжения.
При крутизне откоса больше предельной происходит обрушение его части по поверхности, которую без большой погрешности можно принять за круглоцилиндрическую с радиусом 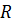 (Рисунок 4.1).
(Рисунок 4.1).
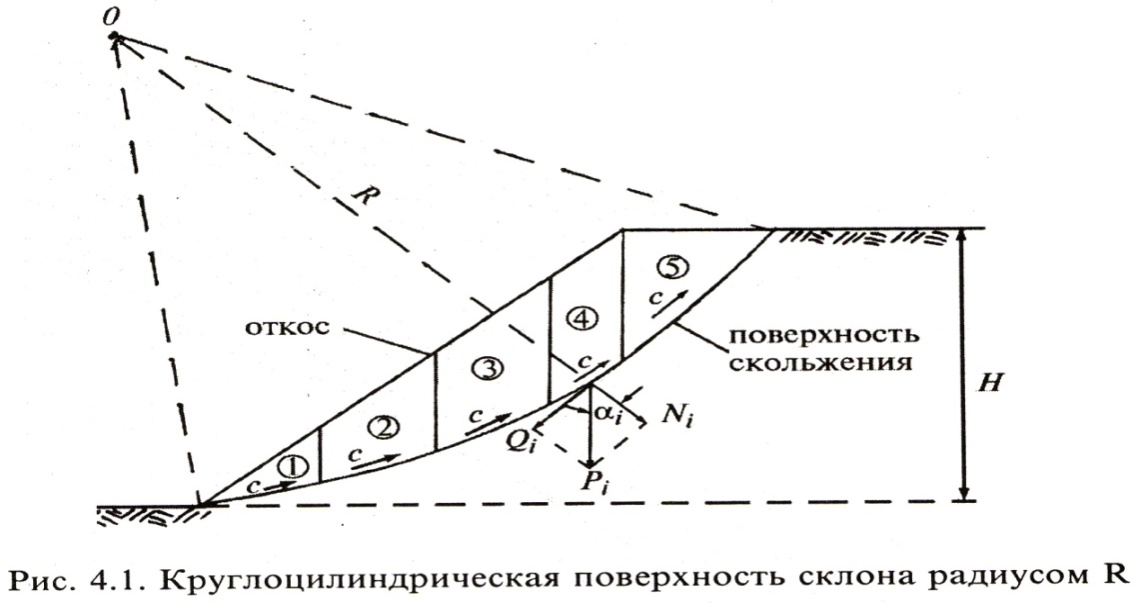
Считая задачу плоской, толщина расчётного откоса по направлению его протяжённости принимается 1 м. На плоскости чертежа след поверхности скольжения имеет вид части окружности радиуса 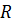 с центром в точке
с центром в точке 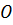 .
.
Степень устойчивости откоса оценивается по величине коэффициента, представляющего собой отношение суммы моментов сил (относительно центра в точке 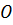 ), удерживающих призму обрушения в устойчивом состоянии -
), удерживающих призму обрушения в устойчивом состоянии - 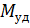 , к сумме моментов сил, вызывающих потерю устойчивости призмы обрушения -
, к сумме моментов сил, вызывающих потерю устойчивости призмы обрушения - 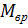 ;
;
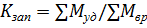 .
.
Для обеспечения устойчивости склона или откоса необходимо, чтобы коэффициент запаса устойчивости 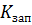 был больше 1. В зависимости от класса ответственности сооружения требуемая величина коэффициента запаса устойчивости
был больше 1. В зависимости от класса ответственности сооружения требуемая величина коэффициента запаса устойчивости 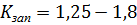 и регламентируется соответствующими типу и классу сооружения нормами (СНиП).
и регламентируется соответствующими типу и классу сооружения нормами (СНиП).
Решение задачи осложняется непосредственностью положения центра вращения, 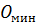 для которого значение коэффициента запаса
для которого значение коэффициента запаса 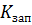 будет иметь минимальное значение из всех возможных значений. Для облегчения определения расположения центра
будет иметь минимальное значение из всех возможных значений. Для облегчения определения расположения центра 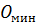 предложен ряд приёмов. Наименее трудоёмким для однородных откосов является способ определения координат положения центра
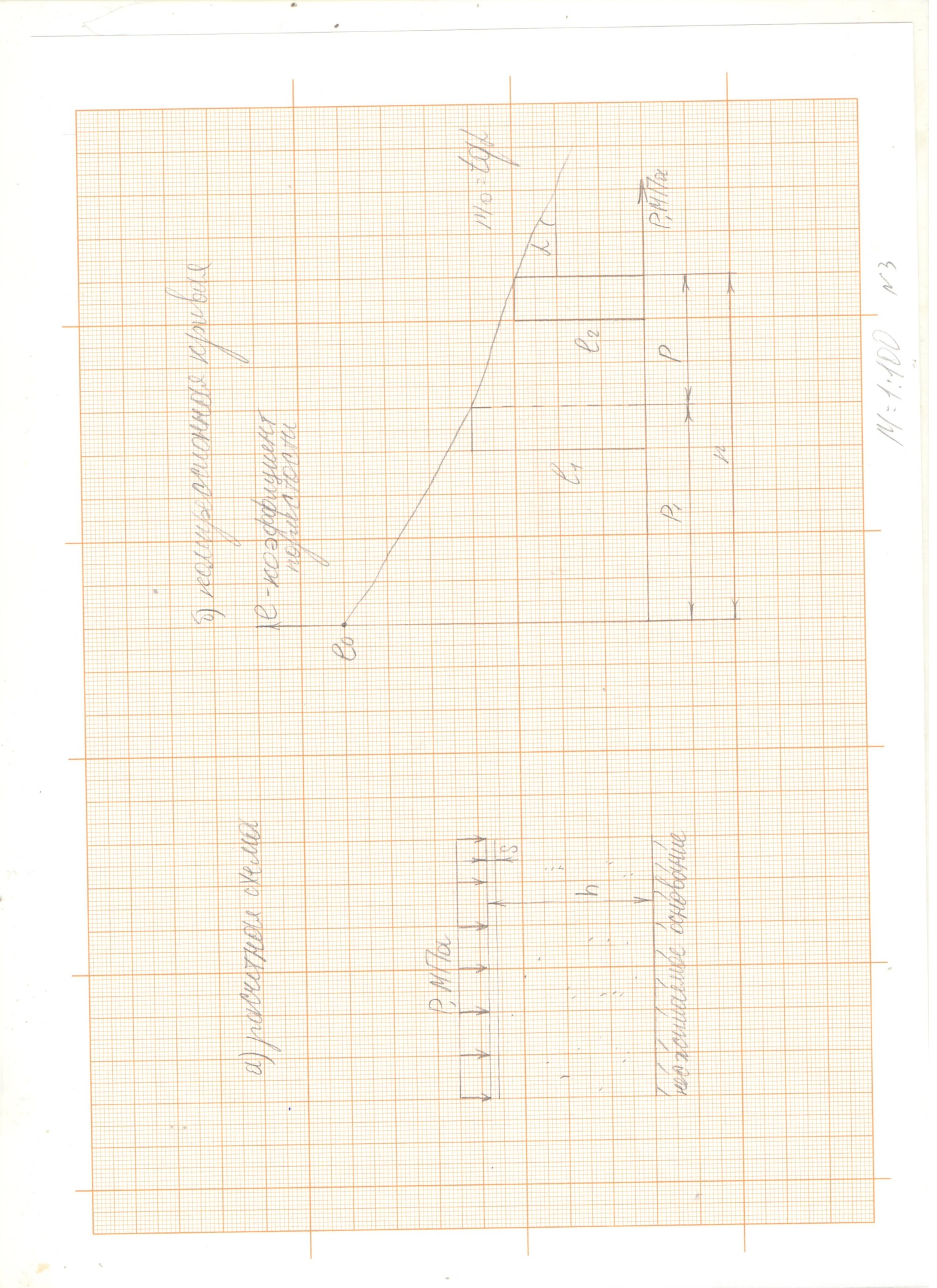
предложен ряд приёмов. Наименее трудоёмким для однородных откосов является способ определения координат положения центра 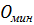 по графику норвежского учёного Ямбу (Рисунок 4.2).
по графику норвежского учёного Ямбу (Рисунок 4.2).
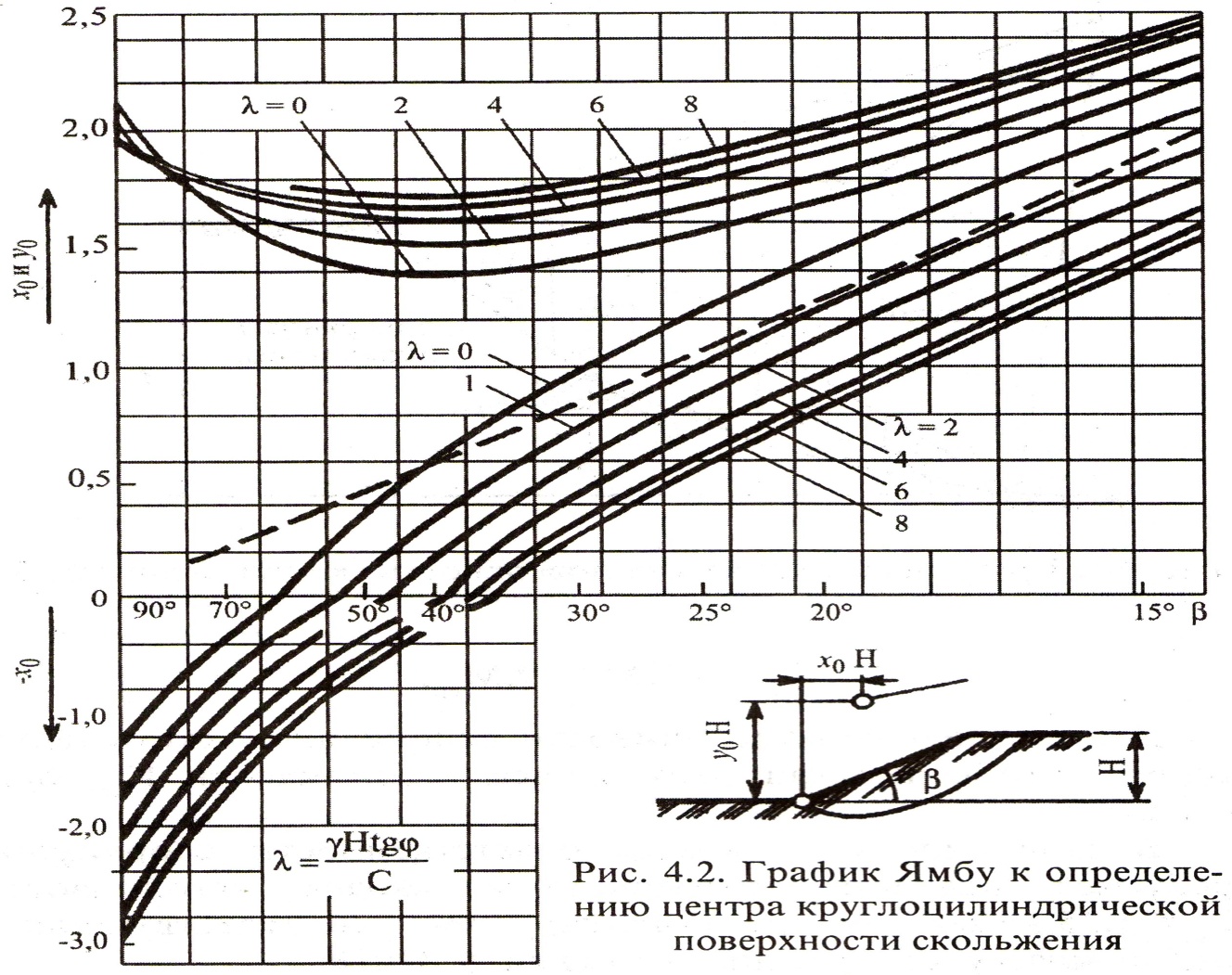
В данном способе по углу наклона откосной линии к горизонту 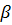 и обобщённому показателю:
и обобщённому показателю:
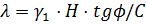 ,
,
Определяют относительные координаты  и
и 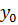 центра вращения
центра вращения 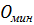 . Абсолютные координаты центра вращения при этом равны:
. Абсолютные координаты центра вращения при этом равны:
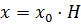 ,
, 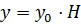 .
.
Точку начала координат помещают в точку пересечения линии откоса с горизонтальной линией основания. Ось абсцисс (ось 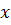 ) с положительными значениями
) с положительными значениями 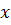 направляют вправо от начала координат, ось ординат (ось
направляют вправо от начала координат, ось ординат (ось 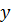 ) – вертикально вверх. Радиус
) – вертикально вверх. Радиус 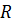 поверхности скольжения определяется по расстоянию от центра вращения
поверхности скольжения определяется по расстоянию от центра вращения 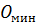 до точки пересечения нижнего горизонта откоса и откосной линии (начала координат). Радиусом
до точки пересечения нижнего горизонта откоса и откосной линии (начала координат). Радиусом 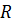 из точки
из точки 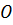 проводят в пределах тела откоса часть круглоцилиндрической поверхности скольжения, определяющей очертание потенциально опасной призмы обрушения.
проводят в пределах тела откоса часть круглоцилиндрической поверхности скольжения, определяющей очертание потенциально опасной призмы обрушения.
Для определения коэффициента запаса устойчивости призма обрушения разбивается на ряд блоков с соблюдением ряда правил:
- поверхность скольжения в пределах одного блока должна находиться в грунте одного типа и состояния;
- вертикальные границы между смежными блоками должны проходить через точки перелома очертания откосной линии (если поверхность откоса имеет сложное очертание);
- целесообразно при разбивке призмы обрушения на расчётные блоки ширину блоков принимать одинаковой.
Вес каждого блока  определяют как:
определяют как:
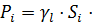 l, где:
l, где:
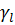 - удельный вес грунта в пределах блока, кН/м3;
- удельный вес грунта в пределах блока, кН/м3; 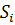 - площадь
- площадь 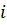 -го блока, определяется как площадь трапеции или треугольника, м2;l- толщина
-го блока, определяется как площадь трапеции или треугольника, м2;l- толщина 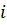 -го блока, равна 1,0 м. Вес каждого блока
-го блока, равна 1,0 м. Вес каждого блока  раскладывается на нормальную
раскладывается на нормальную 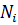 и касательную
и касательную 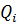 составляющие, приложенные в точке пересечения линии действия силы тяжести с поверхностью скольжения:
составляющие, приложенные в точке пересечения линии действия силы тяжести с поверхностью скольжения:
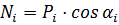 ,
,
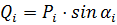 , где:
, где:
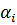 - угол между направлением нормали к поверхности скольжения
- угол между направлением нормали к поверхности скольжения 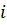 -го блока (в точке пересечения линии действия силы тяжести и поверхности скольжения) и линией действия силы тяжести (веса)
-го блока (в точке пересечения линии действия силы тяжести и поверхности скольжения) и линией действия силы тяжести (веса) 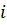 -го блока. Сила сопротивления сдвигу по поверхности скольжения в пределах
-го блока. Сила сопротивления сдвигу по поверхности скольжения в пределах 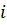 -го блока, обусловленная внутренним трением, определяется по формуле:
-го блока, обусловленная внутренним трением, определяется по формуле:
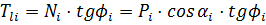 .
.
Сила сопротивления сдвигу по поверхности скольжения в пределах блока, обусловленная действием сцепления с грунтом:
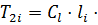 l , где:
l , где:
 - длина дуги поверхности скольжения в пределах расчётного блока (принимается по хорде). Тогда:
- длина дуги поверхности скольжения в пределах расчётного блока (принимается по хорде). Тогда:
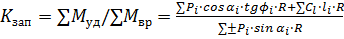 или сокращая на
или сокращая на 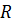 :
:
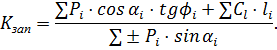
При откосе сложенном однородным грунтом:
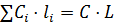 , где:
, где:
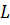 - длина дуги поверхности скольжения, м.
- длина дуги поверхности скольжения, м.
Решение:
Определяем обобщенный показатель по формуле:
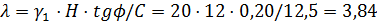 .
.
По графику Ямбу (Рисунок 4.2) определяем координаты центра тяжести вращения 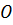 :
:
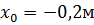 ;
; 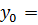 1,6м;
1,6м;
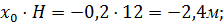
 1,6·12=19,2м.
1,6·12=19,2м.
Радиусом 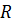 =19,4 м из центра
=19,4 м из центра 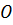 проводится поверхность скольжения. Радиус
проводится поверхность скольжения. Радиус 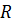 поверхности скольжения определяется по расстоянию от центра вращения
поверхности скольжения определяется по расстоянию от центра вращения 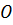 до точки пересечения нижнего горизонта откоса и откосной линии.
до точки пересечения нижнего горизонта откоса и откосной линии.
Оползневое тело (призма обрушения) разбивается на ряд блоков (не менее 5-ти). Определяется длина поверхности скольжения в пределах каждого блока  , угол
, угол 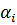 (по тангенсу угла наклона),
(по тангенсу угла наклона), 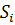 - площадь
- площадь 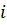 -го блока, а также
-го блока, а также  ;
; 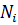 ;
; 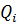 :
:
Определяем вес каждого блока 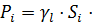 l:
l:
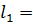 4 м;
4 м; 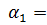 150;
150; 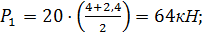
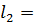 4,2 м;
4,2 м; 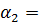 250;
250; 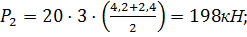
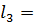 4,2 м;
4,2 м; 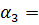 320;
320; 
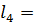 4,2 м;
4,2 м; 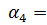 420;
420; 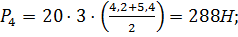
 5,6 м;
5,6 м; 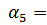 570;
570; 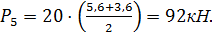
Вес каждого блока раскладывается на нормальную 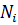 и касательную
и касательную 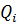 составляющие, приложенные в точке пересечения линии действия силы тяжести с поверхностью скольжения.
составляющие, приложенные в точке пересечения линии действия силы тяжести с поверхностью скольжения.
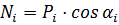 ;
; 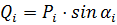 :
:
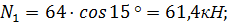
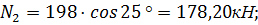
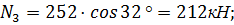
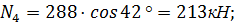
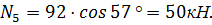
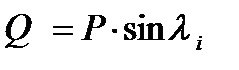
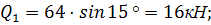
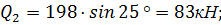
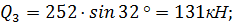
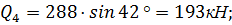
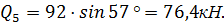
Коэффициент запаса устойчивости 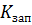 вычисляется по формуле:
вычисляется по формуле:
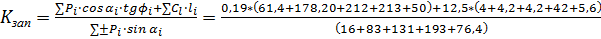 =0,82.
=0,82.
В зависимости от класса ответственности сооружения требуемая величина коэффициента запаса устойчивости 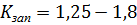 .
.
Из расчета следует, что устойчивость склона не обеспечивается при Кзап=0.82. Необходимо внести некоторые изменения в конструкцию откоса: изменение крутизны склона относительно горизонта, уменьшение нагрузки на брустер, изменение высоты откоса, уменьшение протекания воды через откос. Расчётная схема склона представлена на миллиметровой бумаге.

Задача №5 вариант №5
Расчёт устойчивости массивной подпорной стены.
Исходные данные:
Расчётные размеры массивной подпорной стены: 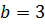 м,
м, 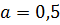 м,
м, 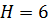 м,
м, 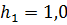 м; параметры сопротивления сдвигу грунта засыпки:
м; параметры сопротивления сдвигу грунта засыпки: 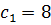 кПа,
кПа, 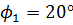 ;
; 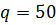 кН/м;
кН/м; 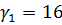 кН/м3.
кН/м3.
Подпорные стенки сооружают в случаях, когда необходимо поддержать массив грунта в равновесии и когда устройство искусственного откоса невозможно.
При гравитационных (массивных) подпорных стенах устойчивость на сдвиг обеспечивается их весом 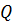 , а горизонтальная составляющая давления грунта воспринимается силой трения
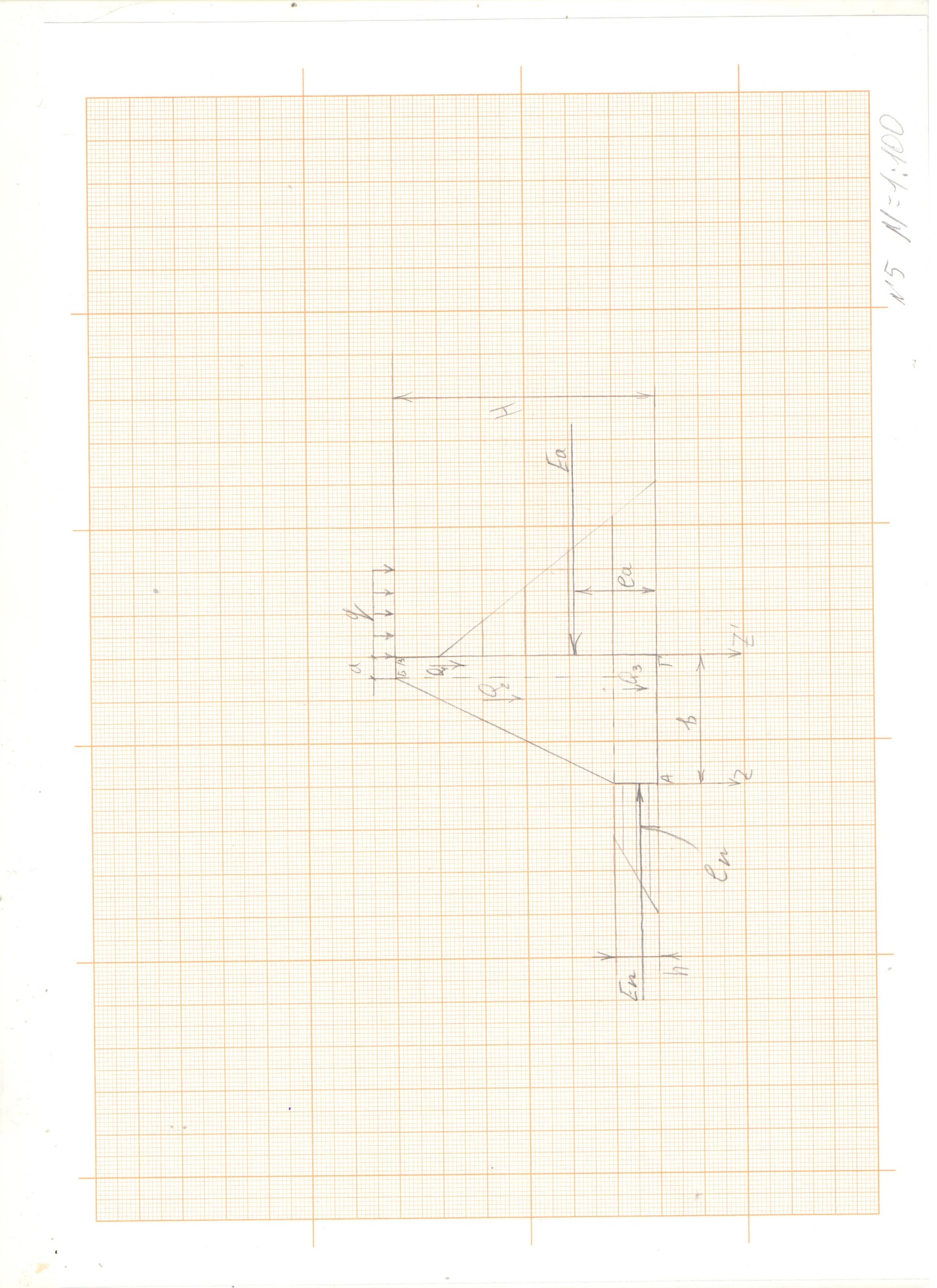
, а горизонтальная составляющая давления грунта воспринимается силой трения 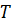 , развивающейся в плоскости подошвы стены (Рисунок 5.1)
, развивающейся в плоскости подошвы стены (Рисунок 5.1)
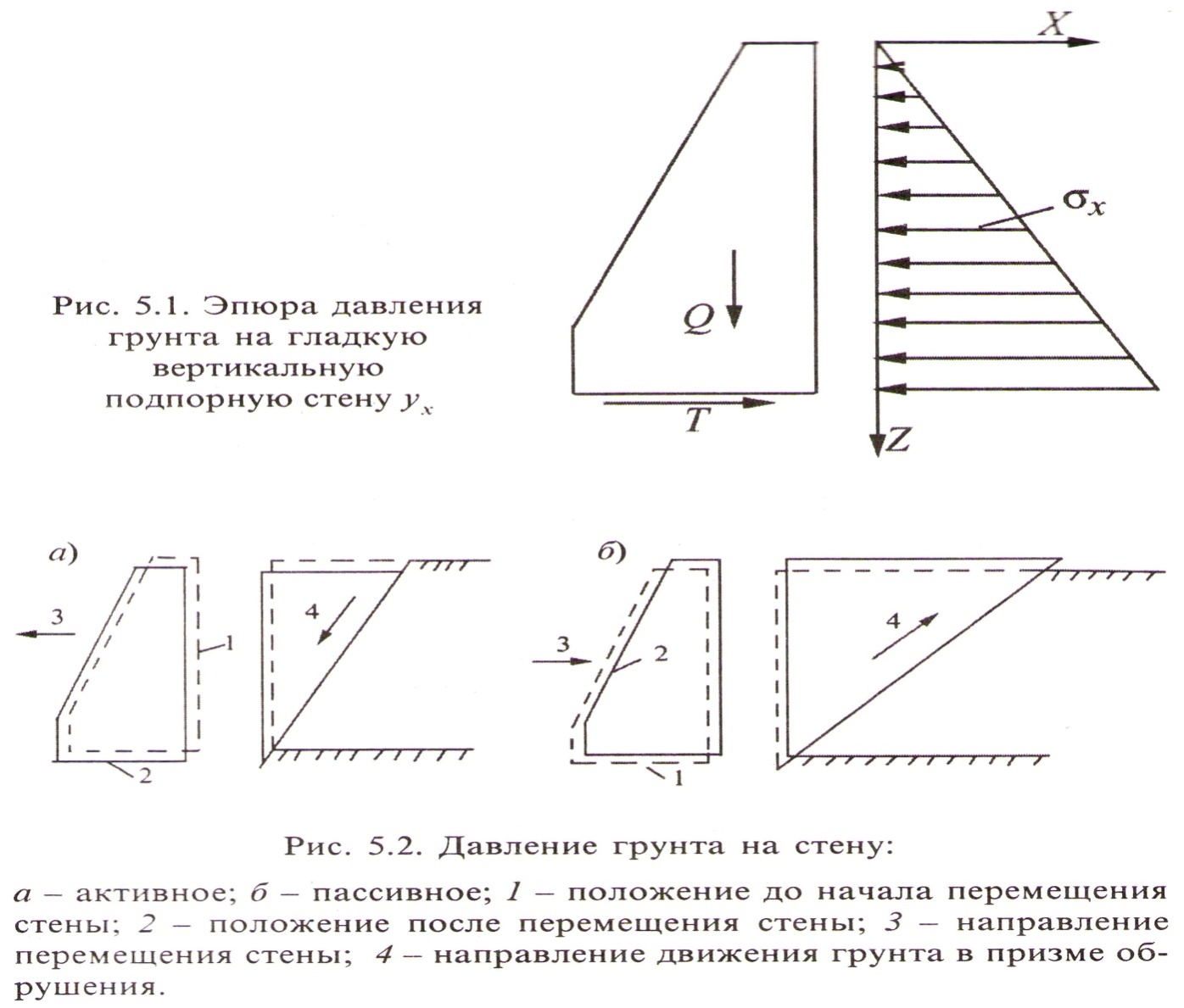
Активным называется давление грунта на подпорную стену, проявляющееся в том случае, если стена имеет возможность переместиться в сторону от засыпки (Рисунок 5.2, а).
Пассивным называется максимальное из всех возможных для данной стены давление её на грунт, проявляющееся в том случае, если стена имеет возможность перемещаться в сторону засыпки под действием внешних сил (Рисунок 5.2, б).
Решение:
Определим 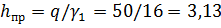 м.
м.
Определяем величину 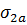 по формуле:
по формуле:
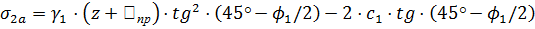 , где:
, где:
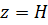
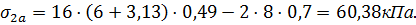
Определяем ординату, 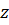 при которой значение
при которой значение 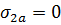 по формуле:
по формуле:
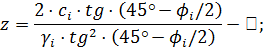
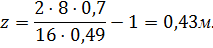
Определяем величину активного давления 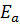 по формуле:
по формуле:
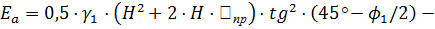
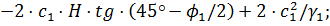
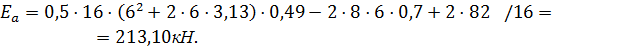
Определяем точку приложения силы 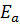 от подошвы фундамента стены по формуле:
от подошвы фундамента стены по формуле:
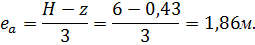
Строим эпюру пассивного давления по формуле:
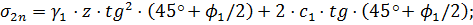
При 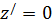 м;
м;
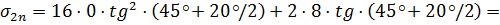
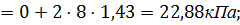
При 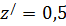 м;
м;
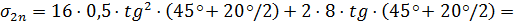
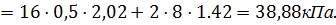
Определим величину пассивного давления по формуле:
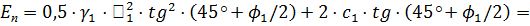
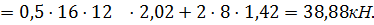
Определим ординату приложения силы 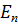 от подошвы фундамента стены по формуле:
от подошвы фундамента стены по формуле:
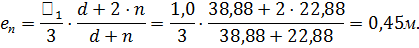
Определим вес 1 погонного метра подпорной стены по формуле:
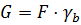 , где:
, где:
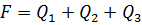 - площадь сечения АБВГ;
- площадь сечения АБВГ;
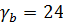 кН/м3- удельный вес бетона.
кН/м3- удельный вес бетона.
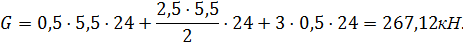
Проверим устойчивость стены против опрокидывания относительно точки «А»
Коэффициент устойчивости стены против опрокидывания 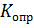 равен отношению суммы моментов сил удерживающих
равен отношению суммы моментов сил удерживающих 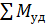 к сумме моментов сил
к сумме моментов сил 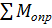 , опрокидывающих стену относительно ребра «А». Этот коэффициент не должен быть меньше 1,5.
, опрокидывающих стену относительно ребра «А». Этот коэффициент не должен быть меньше 1,5.
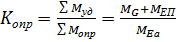 , где:
, где:
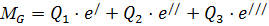 ;
;
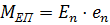 - момент сил удерживающих стену;
- момент сил удерживающих стену;
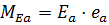 - момент сил опрокидывающих стену.
- момент сил опрокидывающих стену.
Следовательно, коэффициент устойчивости стены против опрокидывания 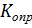 определим по формуле:
определим по формуле:
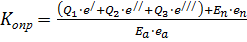 ;
;
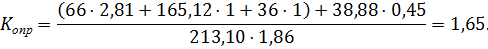
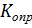 больше1, устойчивость стены на опрокидывание обеспечена с достаточным запасом.
больше1, устойчивость стены на опрокидывание обеспечена с достаточным запасом.
Проверяем устойчивость стены на плоский сдвиг.
Кроме силы 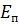 , сдвигу сопротивляется сила трения
, сдвигу сопротивляется сила трения 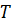 по подошве стены, которую определим по формуле:
по подошве стены, которую определим по формуле:
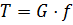 , где:
, где:
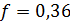 - коэффициент трения для песчаных и крупнообломочных грунтов;
- коэффициент трения для песчаных и крупнообломочных грунтов;

Коэффициент устойчивости против сдвига 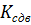 , равен отношению суммы проекций на подошву фундамента сил удерживающих к сумме проекций сил сдвигающих и не должен быть меньше 1,3:
, равен отношению суммы проекций на подошву фундамента сил удерживающих к сумме проекций сил сдвигающих и не должен быть меньше 1,3:
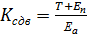 ;
;
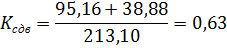
Устойчивость стены заданных размеров против сдвига не обеспечена и необходимо внести изменения в конструкцию стены.
Увеличим размер стеныа до размера 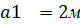
размер 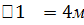
Определим значение 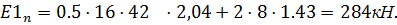
Значение 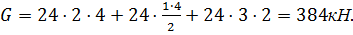
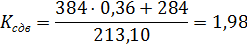
Вывод: изменение размеров стены обеспечивает устойчивость стены на сдвиг. Обеспечение устойчивости стены на опрокидывание автоматически выполнено.
Задача №6 вариант №6
Определение давления грунта на подземный трубопровод.
Исходные данные:
Диаметр трубопровода: 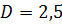 м; глубина залегания трубопровода:
м; глубина залегания трубопровода:
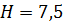 м; ширина траншеи:
м; ширина траншеи: 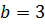 м; тип грунта- суглинок слабый;
м; тип грунта- суглинок слабый;
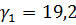 кН/м3; соотношение
кН/м3; соотношение 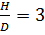 ,
, 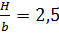
Задача точного определения давления грунта на трубопровод является весьма сложной, так как величина давления существенным образом завис от способа прокладки трубопровода, его жёсткости и конфигурации.
Так, если допустить, что устройство трубопровода не вносит изменений в напряжённое состояние окружающего массива, то трубопровод будет испытывать давление грунта, которое определяется зависимостями (Рисунок 6.1):
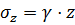 ;
;
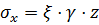 .
.
Однако прокладка трубопровода в той или иной степени нарушает естественное напряжённое состояние массива, что оказывает значительное влияние на величину давления грунта.
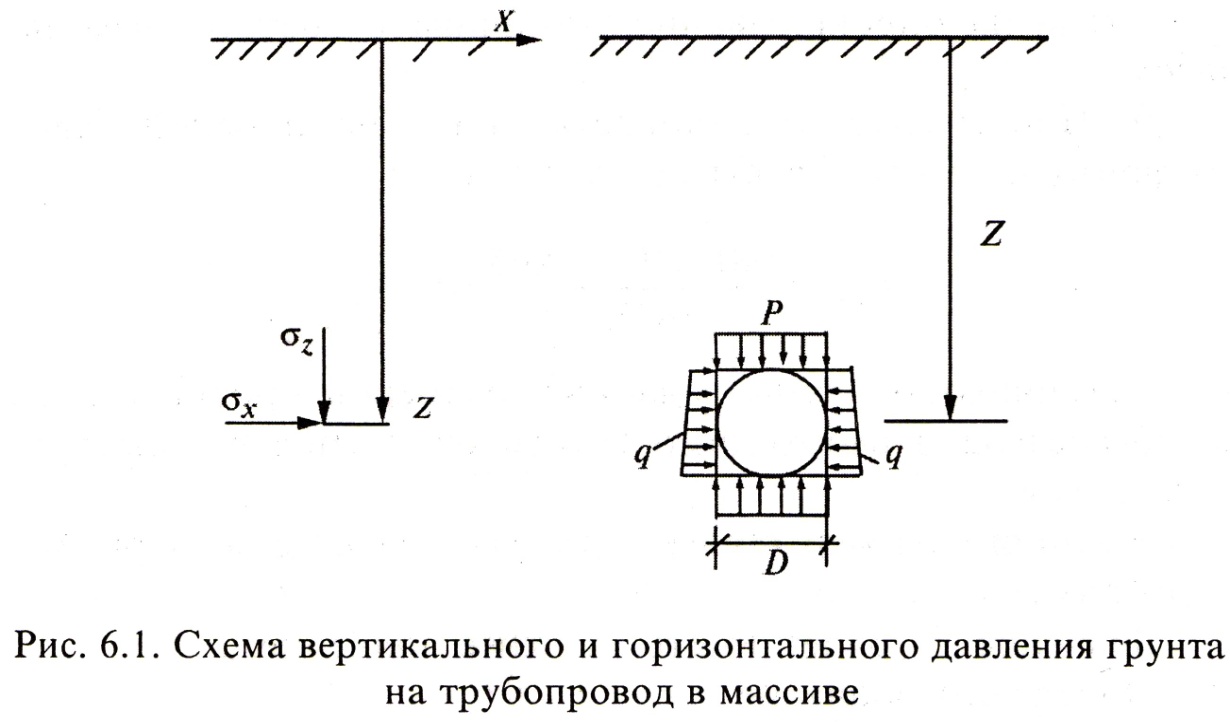
Следует различать три потенциальных способа прокладки трубопроводов: под насыпью (Рисунок 6.2, а), в траншее (Рисунок 6.2, б) и с помощью закрытой проходки (прокола) или горным способом (Рисунок 6.2, в).
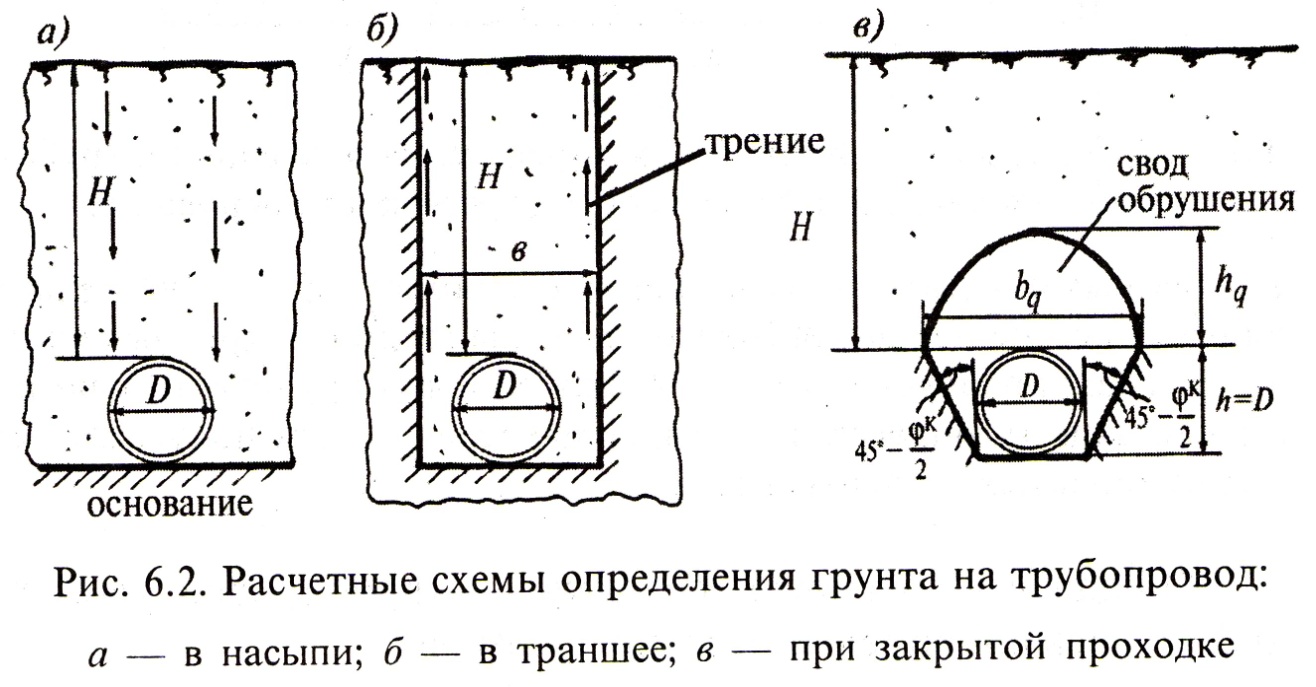
Для трёх способов прокладки трубопроводов (при одинаковой глубине их заложения  ) давление
) давление 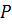 будет различным: при траншейной укладке
будет различным: при траншейной укладке 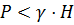 ; в насыпи
; в насыпи 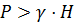 ; при закрытой проходке
; при закрытой проходке 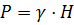 , а при большой глубине заложения – как горное давление с учётом так называемого свода обрушения.
, а при большой глубине заложения – как горное давление с учётом так называемого свода обрушения.
Это происходит по следующим причинам. Если трубопровод прокладывается в траншее, то грунт, находящийся сбоку от траншеи уже ранее уплотнился под действием собственного веса. Грунт, который засыпается в траншею после укладки трубопровода, будет более рыхлым и ещё не уплотнившимся под действием собственного веса.
В связи с этим, при уплотнении грунта засыпки и его осадкам, по бортам траншеи возникает сила трения. Грунт засыпки как бы зависает на стенках траншеи и тем более, чем больше будет глубина траншеи. Для трубопроводов, закладываемых в насыпи, силы трения грунта будут иметь противоположное направление, чем расположенный с ними рядом грунт, уплотняющийся под действием собственного веса.
Расчёт нормативного давления грунта
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|