
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вологодский государственный университет»
федеральное государственное бюджетное образовательное учреждение высшего образования
«Вологодский государственный университет»
 |
Институт машиностроения ,энергетики и транспорта
(наименование института)
 |
Кафедра Электрооборудования
(наименование кафедры)
КОНТРОЛЬНАЯ РАБОТА
Дисциплина: «Физика »

Наименование темы: « »
Шифр работы КР 13.03.02 44.02 10 2020
код специальности/направления код кафедры регистрационный номер по журналу год
| Руководитель ст.пр. Мелконян Ш.Р. |
| (уч. степень, звание, должность. Ф.И.О) |
| Выполнил (а) студент Тарабухин В.О. |
| (Ф.И.О) |
| Группа, курс 5Б13 ЭО – 15ЗУ , 1 Курс |
| Дата сдачи |
| Дата защиты |
| Оценка по защите |
| (подпись преподавателя) |
Вологда
2020 г.
10. Точка движется по окружности радиусом R= 30 см с постоянным угловым ускорением. Определить тангенциальное ускорение 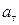 точки, если известно, что за время 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение
точки, если известно, что за время 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение 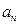 =2,7 м/с2.
=2,7 м/с2.
Дано:
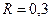 м
м
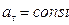
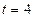 с
с
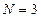
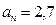 м/с2
м/с2
Найти: 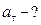
Решение:
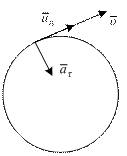
Нормальное ускорение 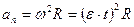 . Тангенциальное ускорение
. Тангенциальное ускорение 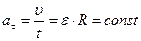 .
.
Тогда 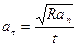 . Находим числовое значение:
. Находим числовое значение: 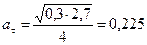 м/с2.
м/с2.
Ответ: 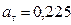 м/с2.
м/с2.
40. Материальная точка массой m=2 кг двигалась под действием некоторой силы согласно уравнению 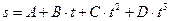 , где А=10 м, В= –2 м/с, С=1 м/с2, D= –0,2 м/с3. Найти мощность, развиваемую при движении, в моменты времени
, где А=10 м, В= –2 м/с, С=1 м/с2, D= –0,2 м/с3. Найти мощность, развиваемую при движении, в моменты времени 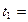 2 c и
2 c и 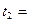 5 c.
5 c.
Дано:
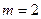 кг
кг
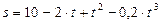
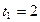 с
с
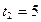 с
с
Найти: 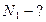 ,
, 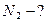
Решение:
Мощность двигателя: 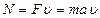 . Скорость
. Скорость 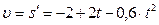 .
.
Ускорение 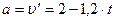 . Тогда
. Тогда 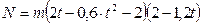 .
.
Находим числовые значения:
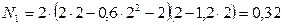 Вт,
Вт,
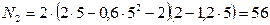 Вт.
Вт.
Ответ: 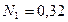 Вт,
Вт, 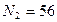 Вт.
Вт.
30. Два груза массами m1=10 кг и m2=15 кг подвешены на нитях длиной l=2 м так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол 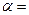 600 и отпущен. На какую высоту поднимутся оба груза после удара? Удар считать неупругим.
600 и отпущен. На какую высоту поднимутся оба груза после удара? Удар считать неупругим.
Дано:
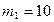 кг
кг
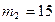 кг
кг
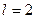 м
м
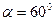
Найти: 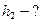
Решение:
Согласно закону сохранения энергии 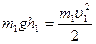 , где высота на которую подняли меньший груз
, где высота на которую подняли меньший груз 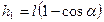 . Тогда
. Тогда 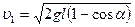 .
.
Согласно закону сохранения импульса 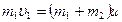 .
.
Учитывая, что 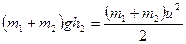 , запишем
, запишем 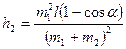 .
.
Находим числовое значение: 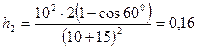 м.
м.
Ответ: 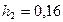 м.
м.
20. Тело массой 0,2 кг движется прямолинейно, причем координата изменяется по закону x=A–Bt+5t2–t3 (время – в секундах, координата – в метрах). Найти силу, действующую на тело в конце второй секунды движения.
Дано:
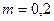 кг
кг
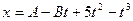
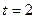 c
c
Найти: 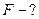
Решение:
По второму закону Ньютона 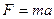 , где ускорение
, где ускорение 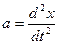 .
.
Тогда 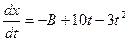 , далее
, далее 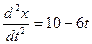 . Откуда
. Откуда 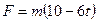 .
.
Находим числовое значение: 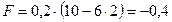 Н.
Н.
Ответ: 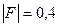 Н.
Н.
90. Определить скорость течения воды в широкой части горизонтально расположенной трубы переменного сечения, если радиус узкой части в 3 раза меньше радиуса широкой части, а разность давлений в широкой и узкой частях трубы 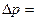 10 кПа.
10 кПа.
Дано:
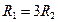
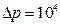 Па
Па
Найти: 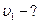
Решение:
Уравнение неразрывности струи: 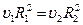 . Согласно уравнению Бернулли:
. Согласно уравнению Бернулли: 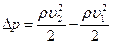 .
.
Тогда 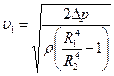 . Находим числовое значение:
. Находим числовое значение: 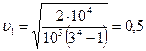 м/с.
м/с.
Ответ: 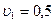 м/с.
м/с.
100. Медный шарик диаметром d=1 см падает с постоянной скоростью в касторовом масле. Является ли движение масла, вызванное падением в нем шарика, ламинарным? Критическое значение числа Рейнольдса Re=0,5.
Дано:
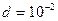 м
м
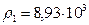 кг/м3
кг/м3
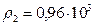 кг/м3
кг/м3
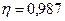 Па·с
Па·с
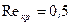
Найти: 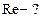
Решение:
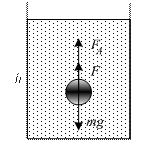
По второму закону Ньютона 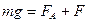 , где
, где 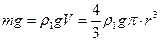 .
.
Сила Архимеда 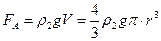 . Сила сопротивления
. Сила сопротивления 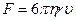 .
.
Тогда 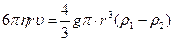 . Число Рейнольдса
. Число Рейнольдса 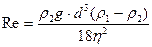 .
.
Находим числовое значение: 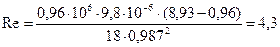 .
.
Ответ: движение жидкости турбулентное.
110. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа А=6,9 Дж. Длина стержня l=1 м, площадь поперечного сечения S=1 мм2, модуль Юнга для алюминия Е=69 ГПа.
Дано:
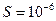 м2
м2
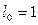 м
м
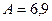 Дж
Дж
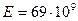 Па
Па
Найти: 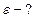
Решение:
Относительное удлинение 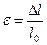 .
.
Работа растяжения 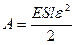 . Тогда
. Тогда 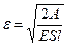 .
.
Находим числовое значение: 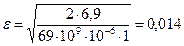 .
.
Ответ: 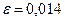 .
.
120. Два сосуда соединены трубкой с краном. В одном находится кислород массой m1=1,8 кг под давлением p1=250 кПа, а в другом – углекислый газ массой m2=4,3 кг под давлением p2=720 кПа. После открывания крана и перемещения газов давление смеси стало равным p. Температура газов до и после перемешивания одинакова. Определить давление p.
Дано:
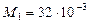 кг/моль
кг/моль
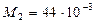 кг/моль
кг/моль
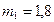 кг
кг
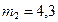 кг
кг
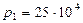 Па
Па
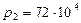 Па
Па
Найти: 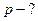
Решение:
По закону Дальтона 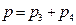 .
.
Согласно условию температура газов постоянна и масса газов неизменна, тогда воспользуемся законом Бойля-Мариотта для изотермического процесса: 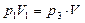 и
и 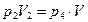 .
.
Тогда 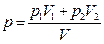 . Из уравнения Менделеева-Клапейрона:
. Из уравнения Менделеева-Клапейрона: 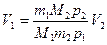 .
.
Тогда 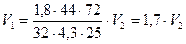 .
.
Находим числовое значение: 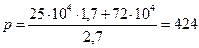 кПа.
кПа.
Ответ: 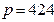 кПа.
кПа.
170. Тонкое кольцо радиусом 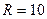 см несет равномерно распределенный заряд
см несет равномерно распределенный заряд 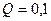 мкКл. На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд
мкКл. На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд 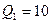 нКл. Какова сила, действующая со стороны заряженного кольца на заряд
нКл. Какова сила, действующая со стороны заряженного кольца на заряд 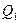 , если он удален от центра на расстояние d1=20 см, d2=2 м?
, если он удален от центра на расстояние d1=20 см, d2=2 м?
Дано:
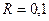 м
м
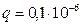 Кл
Кл
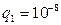 Кл
Кл
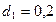 м
м
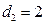 м
м
Найти: 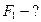 ,
, 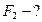
Решение:
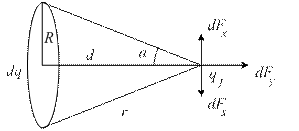
Согласно закону Кулона: 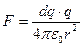 .
.
Откуда 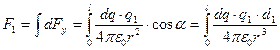 , где
, где 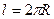 и
и 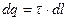 .
.
Тогда 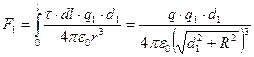 .
.
Находим числовое значение:
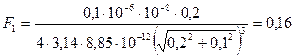 мН.
мН.
Аналогично 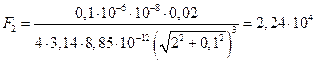 Н.
Н.
Ответ: 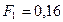 мН,
мН, 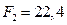 кН.
кН.
180. По двум третям тонкого кольца радиусом 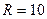 см равномерно распределен зарядс линейной плотностью τ=0,2 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
см равномерно распределен зарядс линейной плотностью τ=0,2 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
Дано:
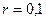 м
м
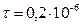 Кл/м
Кл/м
Найти: 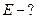
Решение:
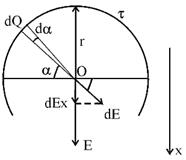
Заряд двух третьих кольца равен 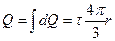 , где
, где 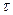 – линейная плотность заряда.
– линейная плотность заряда.
Откуда 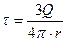 . Напряженность от заряда
. Напряженность от заряда 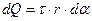 в центре круга равна
в центре круга равна 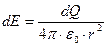 .
.
Ввиду симметрии задачи, суммарная напряженность Е будет направлена вдоль оси х, а другие проекции равны нулю.
Вклад в Е дает только проекция вектора dE на ось х: 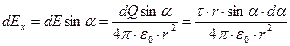 .
.
Полная напряженность 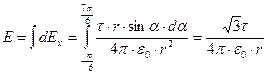 .
.
Находим числовое значение:
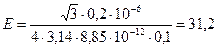 кВ/м.
кВ/м.
Ответ: 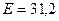 кВ/м.
кВ/м.
190. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость 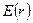 напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1=–σ, σ2=4σ; 2) вычислить напряженность поля в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора напряженности. Принять σ=30 нКл/м2, r=4R; 3) построить график
напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1=–σ, σ2=4σ; 2) вычислить напряженность поля в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора напряженности. Принять σ=30 нКл/м2, r=4R; 3) построить график 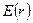 .
.
Дано:
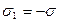
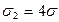
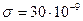 Кл/м2
Кл/м2
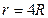
Найти: 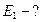 ,
, 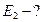 ,
, 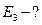 ,
, 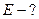 ,
, 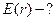
Решение:
1) Из соображений симметрии ясно, что вектор поля Е направлен от оси цилиндров и может зависеть только от расстояния до оси r. Поэтому в качестве замкнутых поверхностей через которые следует вычислять поток поля следует брать соосный цилиндр, так как на его боковой поверхности модуль Е будет неизменным (постоянным) и, следовательно, его можно будет вынести за знак интеграла под которым останется только dS:
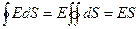 , где S = 2πrh – площадь только боковой поверхности цилиндра, поскольку поток Е через его торцы равен нулю.
, где S = 2πrh – площадь только боковой поверхности цилиндра, поскольку поток Е через его торцы равен нулю.
Тогда внутри меньшего цилиндра (I область, r < R)
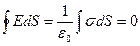 , так как внутри объема r < R зарядов нет. E1S = 0. Откуда Е1 = 0 .
, так как внутри объема r < R зарядов нет. E1S = 0. Откуда Е1 = 0 .
В пространстве между цилиндрами (II область R ≤ r ≤ 2R)
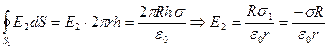 .
.
Вне цилиндров (III область r ≥ 2R) 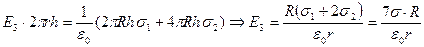 .
.
2) Вычислим поле в заданной точке: 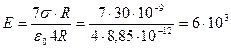 В/м.
В/м.
3) Построим график E(r):
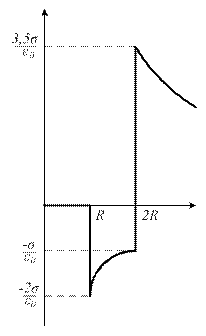
Ответ: : 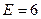 кВ/м.
кВ/м.
200. Диполь с электрическим моментом ре=100 пКл∙м свободно установился в электрическом поле напряженностью Е=200 кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол α=180°.
Дано:
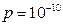 Кл·м
Кл·м
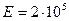 В/м
В/м
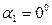
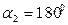
Найти: 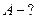
Решение:
Потенциальная энергия диполя в поле равна 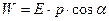 .
.
Тогда 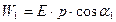 и
и 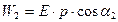 .
.
По закону сохранения энергии работа равна разности потенциальных энергий:
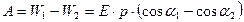 .
.
Находим числовые значения:
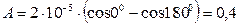 мкДж.
мкДж.
Ответ: 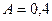 мкДж.
мкДж.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|