Алгебра 9 класс. Тема «Повторение. Вычисления». а2 – в2 = (а – в)(а + в). Как освободиться от иррациональности (квадратного корня) в знаменателе.. Если знаменатель дроби – произведение, содержащее корень, то числитель и знаменатель данной дроби умножаем н

Алгебра 9 класс

Тема «Повторение. Вычисления»

1. Продолжаем повторять свойства арифметического квадратного корня.

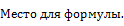
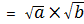
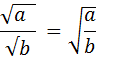
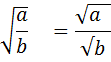
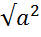= a

Для выполнения следующих заданий из Основного Государственного Экзамена будем использовать формулу разности квадратов:

а2 – в2 = (а – в)(а + в)

(а – в)(а + в) = а² – в²

Задание.

1. Какое из данных ниже чисел является значением выражения?

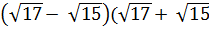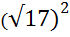
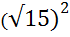) = = 17 – 15 = 2

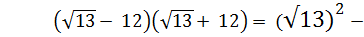12²= 13 – 144 = - 131(видео)

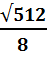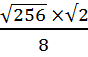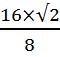2. = = = 2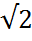

Удобно: при разложении подкоренного выражения на два множителя: надо сначала разделить его на числа, из которых нельзя извлечь корень (2; 3; 5; 6; 7; 10; 11; 13; 14;15…) и определить, можно ли из полученного числа извлечь корень. Если можно, то записать его в виде произведения корней. Например,

= = =

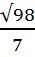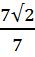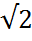
(98 разделим на 2, получим 49. 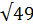= 7, значит множители будут 49 и 2)

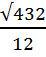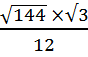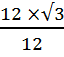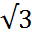= = = (видео)

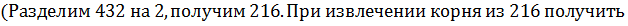
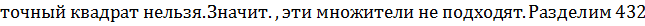
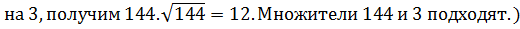
3. Как освободиться от иррациональности (квадратного корня) в знаменателе.

Если знаменатель дроби – произведение, содержащее корень, то числитель и знаменатель данной дроби умножаем на этот корень.

Если знаменатель дроби – сумма (разность), содержащая корень, то числитель и знаменатель дроби умножаем на разность (сумму) этих же выражений. Например,

= =

= = = = = = =

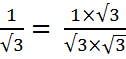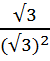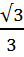
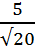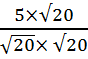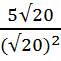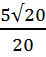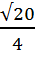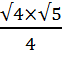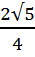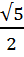
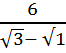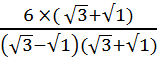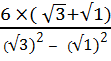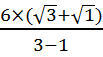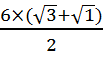= = = = = 3( 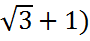(видео).

(Нам надо, чтобы в знаменателе появилась формула разности квадратов. В знаменателе разность 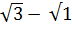, значит, числитель и знаменатель будем умножать на сумму )

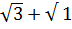Домашнее задание (фото) Выполнить задания к 14 мая.

(Все вычисления выполняем в тетради)