График линейного уравнения с двумя переменными.

Стр 1 из 2Следующая ⇒

График линейного уравнения с двумя переменными.

Вопросы занятия:

· ввести понятие «график линейного уравнения с двумя переменными»;

· рассмотреть поведение графика в зависимости от значений коэффициентов перед переменными.

Материал урока

На прошлом уроке мы с вами познакомились с линейным уравнением с двумя переменным. Давайте, вспомним определение.

И сегодня на уроке мы будем вести речь о графике такого уравнения.

Сформулируем определение:

Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.

Рассмотрим уравнение:

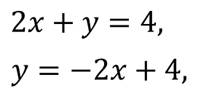
Обратите внимание, что полученная формула имеет вид линейной функции, графиком которой является прямая.

Так как прямая определяется двумя точками, то для построения графика нам достаточно указать две точки. Так:

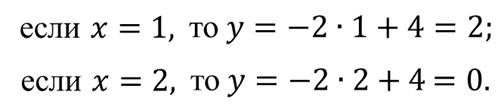
Таким образом, получили две точки с координатами:

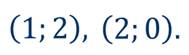
Теперь на координатной плоскости отметим эти точки и проведём через них линию.

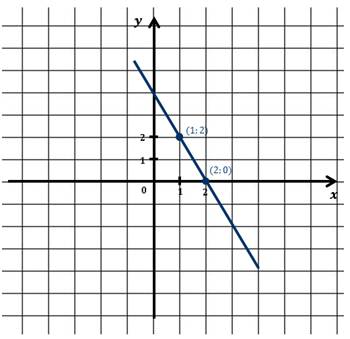
Эта прямая является графиком исходного уравнения.

Все точки, принадлежащие графику, – это пары чисел, которые являются решениями нашего уравнения.

Теперь рассмотрим уравнение, в котором коэффициент при одной из переменных равен нулю.

Например,

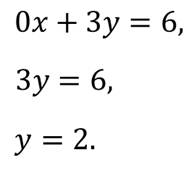
А это постоянная функция. С предыдущих уроков нам известно, что график такой функции – это прямая, которая проходит через точку с координатами (0; 2) и параллельна оси Ox.

Все точки, принадлежащие этой прямой, – это пары чисел, которые являются решениями данного уравнения. И таких решений бесконечно много.

Сформулируем определение.

12 Следующая ⇒