Производная в физике. Производная от координаты по времени есть скорость.. Производная от скорости по времени есть ускорение тела.

Производная в физике

Рассмотрим самый простой случай движения: материальная точка движется по координатной прямой, причём задан закон движения, т. е. координата х этой точки есть известная функция x(t) времени t. За промежуток времени от 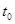до 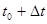перемещение точки равно 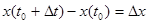, а её средняя скорость такова: .

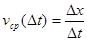Обычно характер движения бывает таким, что при малых 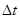средняя скорость практически не меняется, т. е. движение с большей степенью точности можно считать равномерным. Другими словами, значение средней скорости при 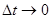стремится к некоторому вполне определённому значению, которое и называют мгновенной скоростью 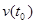материальной точки в момент времени 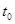. Итак,

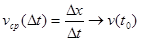при .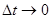

Но по определению производно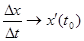й при .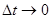

Поэтому считают, что мгновенная скорость v(t) определена (только) для любой дифференцируемой функции x(t), при этом

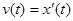Производная от координаты по времени есть скорость.

В этом состоит механический смысл производной.

Аналогичное положение и с ускорением движения. Скорость движения точки есть точки есть функция от времени t. А производная этой функции называется ускорением движения.

.

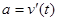Производная от скорости по времени есть ускорение тела.

Пример. Тело движется по прямой так, что расстояние s от начальной точки изменяется по закону 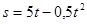(м)., где t – время движения в секундах. Найдите скорость тела через 2 с после начала движения.

Решение.

Скорость тела равна .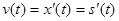

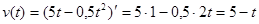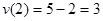(м/с).

Ответ: 3 м/с.

Домашнее задание.

№ 267. Материальная точка движется прямолинейно по закону .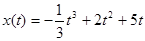

а) Выведите формулу для вычисления скорости движения в любой момент времени t.

б) Найдите скорость точки в момент времени 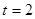с. (Перемещение измеряется в метрах).

в) Через сколько секунд после начала движения точка остановится?

№ 268. Материальная точка движется прямолинейно по закону 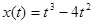. Найдите скорость и ускорение в момент 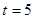с. (Перемещение измеряется в метрах).

№ 269. Вращение тела вокруг оси совершается по закону 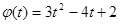/ Найдите угловую скорость ω(t) в произвольный момент времени t и при 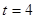с.(φ(t) – угол в радианах, ω(t) – скорость в радианах в секунду, t – время в секундах).