Контакты

Случайная статья

Наибольшее и наименьшее значение функции

Наибольшее и наименьшее значение функции

Решение практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции.

По теореме Вейерштрасса: непрерывная на отрезке 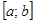функция 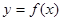принимает на этом отрезке наибольшее и наименьшее значения, т. е. на 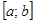существуют точки, в которых 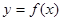принимает наибольшее и наименьшее на 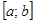значения.

Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.

Пример.Найти наибольшее и наименьшее значение функции 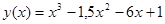на отрезке .

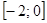Решение.

;

; ;

;

;

; .

; .

;

;

.

; .

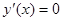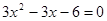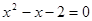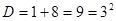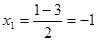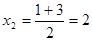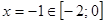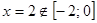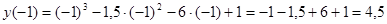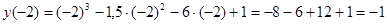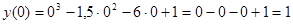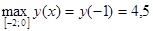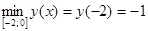Домашнее задание.

№ 305 (а).Найдите наибольшее и наименьшее значение функции 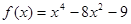на промежутке .

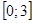№ 305 (б).Найдите наибольшее и наименьшее значение функции 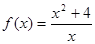на промежутке .

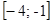№ 305 (в).Найдите наибольшее и наименьшее значение функции 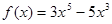на промежутке .

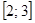© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.