
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
САМОСТОЯТЕЛЬНАЯ РАБОТА №3. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
САМОСТОЯТЕЛЬНАЯ РАБОТА №3
Тема 3.1Алгебраическая и тригонометрическая форма записи комплексного числа
Задание 1. Сложить два комплексных числа z1 = 2 + 5i, z2 = 6 - 7i
Задание 2. Найти произведение комплексных чисел z1 = 8 + 3i, z2 = 4 - i
Задание 3. Перевести комплексное число 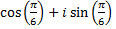 в алгебраическую форму.
в алгебраическую форму.
Задание 4. Перевести комплексное число 13 +5 i в тригонометрическую форму.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Сложение и вычитание комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 осуществляется по правилам сложения и вычитания двучленов (многочленов) x1 + i y1 и x2 + i y2 , т.е. в соответствии с формулами
z1 + z2 = x1 + i y1 + x2 + i y2 = x1 + x2 + i (y1 + y2),
z1 – z2 = x1 + i y1– (x2 + i y2) = x1– x2 + i (y1– y2).
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид: i 2 = – 1 .
По этой причине
z1 z2 = (x1 + i y1) (x2 + i y2) = x1x2 + i x1 y2 + i y1x2 + i 2 y1 y2 =
= x1x2 + i x1y2 + i y1x2 – y1 y2 = x1x2 – y1 y2 + i (x1 y2 + i x2 y1) .
Для того чтобы осуществить переход от тригонометрической формы комплексного числа к алгебраической, необходимо вычислить значения 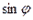 и
и 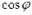 по таблицам значений тригонометрических функций.
по таблицам значений тригонометрических функций.
Для того чтобы осуществить переход от алгебраической формы к тригонометрической, будем использовать следующий алгоритм:
1. Выделить параметры a и b в алгебраической форме 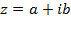 .
.
2. Найти модуль комплексного числа r по формуле: 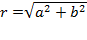 .
.
3. Для нахождения аргумента φ выполнить вспомогательный чертеж и определить четверть, в которой расположен вектор 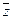 (а, следовательно, и угол φ).
(а, следовательно, и угол φ).
4. В зависимости от четверти, в которой лежит угол φ, воспользоваться одной из следующих формул:
Если 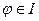 четверти, то четверти, то 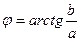 ; ;
| если 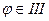 четверти, то четверти, то 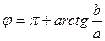 ; ;
|
если 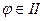 четверти, то четверти, то 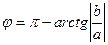 ; ;
| если 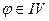 четверти, то четверти, то 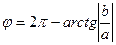 . .
|
5. Подставить найденные значения r и φ в тригонометрическую форму.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|