
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант 1.. Величина - это
Дисциплина: Информатика
Преподаватель: Сорокина Екатерина Анатольевна
Группа: №2, 1 курс (подгруппа 1), МОДСР
Тема урока: ЛК: «Моделирование зависимостей между величинами», ПР№19 «Решение задач. Моделирование зависимостей между величинами».
1. Теория. Уважаемые студенты, изучите, пожалуйста, теоритический материал (напишите краткий конспект).
Перед вами пословицы:
1. Дальше в лес, больше дров.
2. Тише едешь, дальше будешь.
3. Подальше положишь, поближе возьмешь.
4. Как аукнется, так и откликнется.
Все эти пословицы, объединяет одно слово – «Зависимость». Чаще всего с этим понятием, вы встречаетесь на уроках математики и физики.
Зависимость бывает между величинами, которые могут быть прямой и обратной.
Рассмотрим примеры зависимостей:
1) время падения тела на землю зависит от его первоначальной высоты
2) давление газа в баллоне зависит от его температуры
3) уровень заболеваемости жителей города бронхиальной астмой зависит от концентрации вредных примесей в городском воздухе
Всякое исследование нужно начинать с выделения количественных характеристик исследуемого объекта. Такие характеристики называются величинами.
Три основных свойства всякой величины: Имя, значение, тип.
Имя величины: Символическое и смысловое:
Примеры:
Символическое – р, смысловое – давление
Символическое – t, смысловое – время
Если значение величины не изменяется, то она называется постоянной величиной или константой, например: ускорение свободного падения, число п=3,14259, постоянная Планка и др.
Величина, которая может меняться, называется переменной. В описании процесса падения тела переменными величинами являются высота и время падения.
Третьим свойством величины является тип. При изучении баз данных мы уже встречались с типами величин.
Основные типы величин: Числовой, символьный, логический.
Если зависимость между величинами можно представить в математической форме, то мы имеем математическую модель, которая представлена в виде формул. Это примеры моделей, представленных в функциональной форме.
Рассмотрим примеры двух других способов представления зависимостей между величинами: табличного и графического. Представьте, что мы решили проверить закон свободного падения тел экспериментальным путем. Будем бросать стальной шарик с 6-метровой высоты, 9-метровой и т.д., замеряя высоту начального положения шарика и время падения. По полученным результатам составим таблицу и построим график.
В рассмотренном примере мы рассмотрели три способа моделирования зависимости величин.
Это: Функциональный (формула), табличный, графический.
Однако математической моделью падения тела на землю можно назвать только формулу. Она более универсальна, позволяет определить время падения тела с любой высоты. Имея формулу, можно легко создать таблицу и построить график, а наоборот – весьма проблематично.
Информационные модели, которые описывают развитие систем во времени, имеют специальное название: динамические модели.
Пример: зависимость частоты заболеваний жителей города бронхиальной астмой от качества воздуха. Любому человеку понятно, что существует зависимость. Для всех очевидно, что чем хуже воздух, тем больше людей больных астмой. Но это качественное заключение. Для управления уровнем загрязненности воздуха требуются более конкретные знания. Нужно установить, какие именно примеси сильнее всего влияют на здоровье людей, как связана концентрация этих примесей с числом заболеваний. Такую последовательность можно установить посредством сбора многочисленных данных, их анализа и обобщения. Этим занимается статистика.
Статистика – наука о сборе, измерении и анализе массовых количественных данных.
Статистика опирается на сложные математические методы и расчеты, но в арсенале ТП Excel заложены возможности использования этих методов.
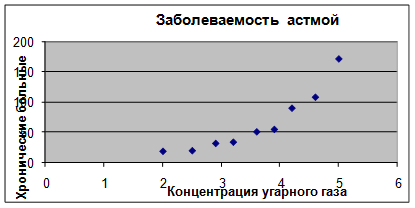
Специалистами собраны сведения из разных городов о средней концентрации угарного газа в атмосфере C и о заболеваемости астмой (число хронических больных на 1000 жителей P.
Рассмотрим табличное и графическое представление статистических данных.
| 
|
Чтобы построить математическую модель данного явления, нужно получить формулу зависимости Р от С.
График искомой функции должен проходить близко к точкам диаграммы экспериментальных данных.
Основные требования к искомой функции:
- она должна быть достаточно простой для использования ее в дальнейших вычислениях;
- график этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек о графика были минимальны и равномерны.
Полученная таким образом функция называется в статистике регрессионной моделью.
2) Получение регрессионной модели происходит в два этапа:
- подбор вида функции;
- вычисление параметров функции.
Чаще всего выбор производится среди следующих функций:
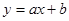 - линейная функция;
- линейная функция;
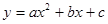 - квадратичная функция;
- квадратичная функция;
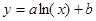 - логарифмическая функция;
- логарифмическая функция;
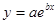 - экспоненциальная функция;
- экспоненциальная функция; 
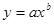 - степенная функция.
- степенная функция.
Во всех этих формулах x – аргумент, y – значение функции, a, b, c – параметры функций.
При выборе одной из функций нужно подобрать параметры так, чтобы функция располагалась как можно ближе к экспериментальным точкам. Существует метод вычисления параметров, он был предложен в 18 веке немецким математиком Гауссом и называется - метод наименьших квадратов (МНК).
Суть – искомая функция должна быть построена так, чтобы сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции была бы минимальна.
Алгоритм работы:
Опишем алгоритм получения с помощью MS Excel регрессионных моделей по МНК с построением тренда. У вас на столах есть алгоритм.
1) Вводим табличные данные.
2) Строим точечную диаграмму, где в качестве подписи к оси OX выбрать текст «Линейный тренд» (остальные надписи и легенду можно игнорировать).
3) Щелкнуть мышью по полю диаграммы; выполнить команду Диаграмма – Добавить линию тренда;
4) В открывшемся окне на закладке «Тип» выбрать «Линейный тренд»;
5) Перейти к закладке «Параметры» и установить галочки на флажках «показать уравнения на диаграмме» и «поместить на диаграмме величину достоверности ампроксикации R^2» и щелкнуть OK.
6) Аналогично получаем и другие тренды.
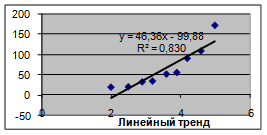
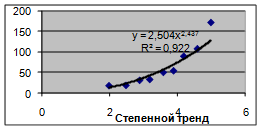
| 
|
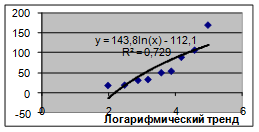
|
R2 ближе всего к 1 у квадратичной модели. Значит, она самая удачная. А самая неудачная – линейная модель.
Мы получили регрессивную математическую модель и можем прогнозировать процесс путем вычислений.
От сюда следует, что выявлять зависимости (создавать модели), нужно:
· для объяснения явлений и процессов
· для прогнозирования процессов
· для управления процессами.
Теперь можно оценить уровень заболеваемости астмой не только для тех значений концентрации угарного газа, которые были получены путем измерений, но и для других значений. Это очень важно с практической точки зрения. Например, если в городе планируется построить завод, который будет выбрасывать в атмосферу угарный газ, то, рассчитав возможную концентрацию газа, можно предсказать, как это отразится на заболеваемость астмой жителей города.
Прогноз бывает двух видов:
восстановление значения внутри области экспериментальных данных (интерполяция)
продолжение линии тренда за границы экспериментальных данных (экстраполяция).
2. Практическая работа (закрепление).
Задание №1. По данным из следующей таблицы постройте с помощью MS Excel линейную, квадратичную, экспоненциальную и логарифмическую регрессионные модели. Определите параметры, выберите лучшую модель.
| X | ||||||||||||||
| Y |
Задние №2. Тестирование
Критерии оценивания теста:
· 6-7 правильных ответов – 5
· 4-5 правильных ответов – 4
· Менее 4 правильных ответов – 3
Вариант 1.
1. Величина - это
а. Количественная характеристика исследуемого объекта;
б. Любое положительное число;
в. Характеристика исследуемого объекта;
г. Любое положительное или отрицательное число.
2. В каком случае говорят о функциональной зависимости между величинами:
а. если зависимость между величинами является полностью определенной;
б. если зависимость носит сложный характер, так как на исследуемую величину влияют множество факторов.
3. Что из предложенного списка не является математической моделью:
а. 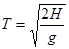
б. 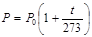
в. нет правильного ответа
4. Информационную модель, которая описывает развитие системы во времени, называют:
а. табличная модель;
б. графическая модель;
в. регрессионная модель
г. динамическая модель
5. Из скольких этапов состоит процесс построения регрессионной модели:
а. два
б. три
в. четыре
г. каждая регрессионная модель уникальна, поэтому точное количество этапов не определено.
6. График регрессионной модели называется:
а. полином
б. тренд
в. экстраполяция
7. Существует два способа прогнозов по регрессионной модели. Если прогноз производится в пределах экспериментальных значений независимой переменной, то он называется:
а. линейной
б. восстановление значений
в. экстраполяция
3. Задание (ответить на вопросы письменно).
1. Как называется график регрессионной модели?
2. Что такое коэффициент детерминированности?
3. Какие значения он принимает?
Практическое задание необходимо отправить на электронную почту до 12:00 –1.05.2020 г.
Почта: kate_sorry94@mail.ru
По всем вопросам звоните по тел. 89835036694, можно писать на WhatsApp/Viber
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|