пошаговые алгоритмы являются средством развития мыслительных процессов младших школьников и одновременно подсказкой при самостоятельном выполнении любого задания.

1.С.Е. ЦАРЕВА «Формирование вычислительных умений в новых условиях» Журнал "Начальная школа" №10/2010 стр 51 https://n-shkola.ru/storage/archive/1405940301-75390570.pdf

процесс формирования вычислительных умений — сложный и многогранный. Он должен основываться на понимании арифметических действий, поэтому последовательность и характер изучения арифметических действий должны быть такими, что" бы при введении действия учащиеся иска" ли ответы на вопрос «Что такое сложение (вычитание, умножение, деление)?», а после получения ответов и овладения смысла" ми действия у них появились бы вопросы: «Как по двум данным числам находить результаты сложения (вычитания, умножения, деления)?» и «Как научиться находить результаты сложения (вычитания, умножения, деления)?».

2. А.М. ЧЕРКАСОВА «Пошаговые алгоритмы при обучении математике» Журнал "Начальная школа" №10/2010 стр 60 https://n-shkola.ru/storage/archive/1405940301-75390570.pdf

3. Т.П. БЫКОВА, «Овладение навыком смыслового чтения как метапредметный результат обучения математике» Журнал "Начальная школа". 2012. № 8 стр 37 https://n-shkola.ru/storage/archive/1405941049-2063091560.pdf

Формирование навыка смыслового чтения при обучении младших школьников математике происходит, прежде всего, в процессе решения текстовых задач. Задание может быть предложено в III классе на уроке повторения и закрепления знаний после того, как изучены таблица умножения, прием нахождения частного методом подбора и проверка деления умножением.

4. Р.Н. ШИКОВА, «Организация самостоятельной деятельности учащихся на уроках математики» Журнал "Начальная школа" 2012. № 2 стр 24https://n-shkola.ru/storage/archive/1405942372-376114601.pdf

В процессе изучения математики должно быть сформировано умение извлекать нужную ин0 формацию из разных источников, включая текст учебника, ориентироваться в справочном материале и самостоятельно изучать доступный по сложности материал по учебнику. Дите решаю различные задачи с помощью умножение и деления для получения ответа.

5. С.Е. ЦАРЕВА «Формирование основ алгоритмического мышления в процессе начального обучения математике» Журнал "Начальная школа" 2012. № 4 стр 5https://n-shkola.ru/storage/archive/1405942147-637020594.pdf

С помощью алгоритма нам показывают этапы действий деления и умножение. Например Алгоритм «Деление с остатком: подбор остатка» (27 : 5, 3 : 4)

1)Развернутая запись.

27 : 5

27 – 3 = 24

24 не делится на 5.

27 – 4 = 23

23 не делится на 5.

27 – 2 = 25

25 : 5 = 5 27 : 5 = 5 (ост. 2)

2) Частично свернутая запись.

27 : 5 27 – 2 = 25

25 : 5 = 5 27 : 5 = 5 (ост. 2)

3) Краткая запись. 27 : 5 = 5 (ост. 2)

6. А.М. ЧЕРКАСОВА, «Опосредованная помощь при развитии познавательной самостоятельности» Журнал "Начальная школа" 2012. № 4 стр 17https://n-shkola.ru/storage/archive/1405942147-637020594.pdf

после объяснения нового материала и коллективного выполнения нескольких типовых заданий учитель требует от учеников самостоятельного выполнения различных видов упражнений. Учитель выдает различные карточки детям, где они проверяют свои знания

Заполни пустые квадраты.

У Тани

У Оли

У Тани кругов больше, чем у Оли, в раза.

У Оли кругов меньше, чем у Тани, в раза.

: = — во столько раз у Тани кругов больше, чем у Оли, или у Оли меньше, чем у Тани.

В карточке поясняется, что ученики узнают в результате деления.

7. Н.Н. ДЕМЕНЕВА, «Формирование универсального действия прогнозирования на уроках математики» Журнал "Начальная школа" 2013. № 9 стр 52https://n-shkola.ru/storage/archive/1405930617-1619290367.pdf

На уроках математики прогнозирование чаще всего связано с предвосхищением результата выполняемых действий, предварительной прикидкой ответа, который должен быть получен при решении задач, уравнений, выполнении измерений. Хорошо известным способом такой прикидки, служащим для осуществления самоконтроля, является определение количества цифр в частном при делении многозначных чисел на однозначные и двузначные.

Примеры заданий «Расставьте порядок действий и вычислите значения выражений (24 + 46) : 5 и 27 + 2*3»

8. Д.А. СЕРГЕЕВА Нестандартные арифметические задачи — одно из средств формирования исследовательских умений Журнал "Начальная школа" 2013 стр 62https://n-shkola.ru/storage/archive/1405337209-979093636.pdf

В этой литературе автор при рассмотрении «Нестандартной арифметической задачи» приводит задачу в которой выполняется деление и иметься графический чертеж:

«На уроке физкультуры все ученики вы+ строились в линейку на расстоянии 1 м друг от друга. Вся линейка растянулась на 12 м. Сколько учеников в классе?»

Учащиеся выполняют действие:

12 : 1 = 12 (уч.).

— Для обработки полученных результа+ тов и проверки гипотезы предлагаю прове+ рить предположение, выполнив чертеж. Учащиеся чертят отрезок длиной 12 клеток и ставят штрихи через 1 клетку.

После задаются вопросы на анализ данного чертежа и правильность использования деления в этой задаче:

— Как узнать, правильно ли мы нашли количество учащихся? (Для этого надо посчитать количество штрихов.) Сколько их? (13.) Совпадает ли данный результат с числом, полученным при делении? (Нет.) Выскажите свое предположение, почему так получилось? (Потому что делением мы нашли количество получившихся отрез+ ков, а не количество необходимых для их построения штрихов, совпадающее с коли+ чеством людей. Надо было сначала постро+ ить чертеж.)

9. И.В. ШАДРИНА «Нестандартные задачи в обучении математике» Журнал "Начальная школа" 2015. № 6 стр 62 https://n-shkola.ru/storage/archive/1405337209-979093636.pdf

В этой статье производиться поиск нужного числа с помощью перебора умножением:

10. О.В. ГАВРИКОВА «Формирование универсальных учебных действий при обучении решению арифметических задач» НАЧАЛЬНАЯ ШКОЛА. 2011. № 8 стр 46https://n-shkola.ru/storage/archive/1407226064-1956194444.pdf

В этой статье говориться о методика обучения решению арифметических задач по программе Н.Б. Истоминой и приводиться задачи с использованием таких действий как деление и умножение :

Так, например, пример предлагается окончить составление задачи используя выражение содержащие умножение, требуя понимания смысла умножения:

Так же приводиться задание дополнение задачи по схеме, а потом и составление по ним выражений, при этом решающие должны понимать смысл деления и умножения :

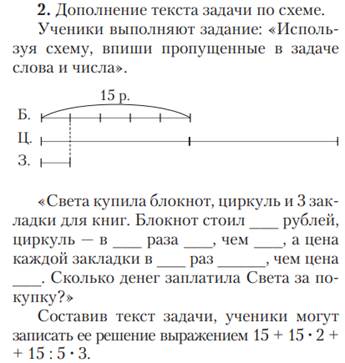
В последней задаче данной статьи предлагается используя схему и текст задачи написать пояснения к выражения содержащие умножение и деление в соответствие со смыслом данной задачи :