Таблица 1.2

ЧИСЛА И КОДЫ

СИСТЕМЫ СЧИСЛЕНИЯ

В дискретной технике вся информация независимо от еe характера представляется в числовой форме, причем используются только позиционные системы счисления. В этих системах любое целое неотрицательное 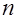-разрядное число записывается в виде последовательности 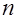цифр .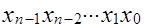

Число 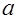различных символов (0, 1, 2, …, 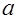-1), принятых для представления цифр, определяет основание системы счисления. Вклад цифры в изображаемое число зависит как от этого основания, так и от занимаемой ею позиции (разряда) в последовательности цифр. Цифра 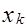входит с весом 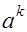и означает 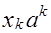, а вся последовательность цифр 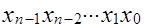выражает в системе счисления с основанием 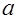число

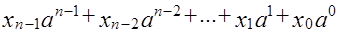Привычная десятичная система ( 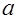=10) использует цифры 0, 1, 2, …, 9, так, что, например: 3175 = 3*10³ + 1*10² + 7*10¹ + 5*10⁰. В вычислительной технике преимущественное значение получила двоичная система счисления, для которой достаточно двух цифр 0 и 1. Двоичный разряд представляет собой наименьшее количество информации, называемое битом. Последовательность двоичных цифр 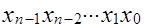служит записью двоичного числа

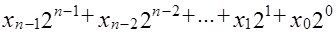Среди других систем счисления чаще всего используются восьмеричная и шестнадцатеричная. В восьмеричной системе цифры изображаются теми же символами, что и в десятичной, а в шестнадцатеричной системе к ним добавляется еще шесть символов 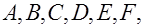которые соответствуют десятичным числам 10, 11, 12, 13, 14, 15. Запись первых 32 чисел в системах счисления с основанием 2, 8 и 16 показаны в табл. 1.1. Если требуется указать основание системы счисления, запись числа сопровождается десятичным индексом. Например:

10110₂=(1*2⁴+1*2³+0*2²+1*2¹+0*2⁰)=26₁₀;

5327₈=(5*8³+3*8²+2*8¹+7*8⁰)=2775₁₀;

2DF9₁₆=(2*16³+13*16²+15*16¹+9*16⁰)=11769₁₀.

Отсюда видно, что для преобразования числа из любой системы счисления в десятичную достаточно вычислить значение соответствующего многочлена, подставив в него десятичные значения разрядов и основания системы счисления. Вычисления удобно выполнять по схеме Горнера, основанной на представлении многочлена в виде:

(…((x_n-1a+x_n-2)a+x_n-3)a+…+x₁)a+x₀,

т.е. цифра х_n-1 старшего разряда переводимого числа умножается на основание а исходной системы счисления и результат суммируется со следующей цифрой, затем этот процесс повторяется, пока не дойдет до цифры младшего разряда.

Например, преобразование восьмеричного числа в десятичное по этой схеме представляется следующим образом:

5327₈ 5.8 + 3 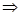43.8 + 2 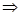346.8 + 7 = 2775₁₀

Наибольшее десятичное число, которое можно представить n- разрядным числом в системе счисления с основанием а, равно (аⁿ–1). При этом для представления аⁿ чисел необходимо по а различных цифр на каждый разряд, т.е. всего q = na цифр. В то же время количество чисел, которые можно представить в системе счисления с основанием а, располагая q цифрами, выражается функцией а^q|a. Она достигает максимума при равенстве а основанию натуральных алгоритмов е» 2,7, что указывает на троичную систему как наиболее экономичную. В своё время этот вывод служил одним из оснований для построения троичных вычислительных машин, но с развитием интегральной технологии он потерял своё значение. В вычислительной технике доминирующую роль по-прежнему играет двоичная система благодаря таким её преимуществам как удобство технической реализации, простота арифметических и логических операций и др. Между тем в информационно-измерительной технике применяются также многозначные элементы и структуры, с помощью которых осуществляются различные операции в десятичной и других системах счисления.

В общем случае, когда число имеет дробную часть, последняя отделяется от целой части разделительным символом – точкой или запятой:

x_n-1x_n-2…x₁x_0,x_-1x_-2…x_-m,

n цифр целой m цифр дробной

части части

что соответствует числу:

x_n-1a^n-1 + x_n-2a^n-2 +…+x₁a¹ + x₀a⁰ +

целая часть числа

+ x_-1a^-1 + x_-2a^-2 +…+x_-ma^-m.

дробная часть числа

Выражение любого числа в десятичной системе сводится к вычислению его многочленного представления, например:

405,37₈=(4*8²+0*8¹+5*8⁰+3*8^-1+7*8^-2)₁₀=261,140625₁₀.

Арифметические операции над числом в любой системе счисления выполняются по тем же правилам, что и в десятичной системе.

Таблица 1.1

Десятич-ное число	В системе счисления с основанием			Десятич-ное число	В системе счисления с основанием
	2	8	16		2	8	16










			A				1A
			B				1B
			C				1C
			D				1D
			E				1E
			F				1F

ПРЕОБРАЗОВАНИЕ ЧИСЕЛ

Чаще всего приходится переводить десятичные числа в двоичные и обратно, что можно выполнить с помощью универсального алгоритма, применяемого раздельно для целой и дробной частей. Перевод целой части десятичного числа в двоичную систему сводится к записи в обратном порядке остатков (0 или 1), получаемых при делении исходного числа и каждого последующего частного на два. Дробная часть получается из целых частей (0 или 1) при ее последовательном умножении на два, причем такое умножение продолжается до тех пор, пока дробная часть обратится в нуль или получится требуемое количество знаков после разделительной точки.

Покажем, например, что 26.3125₁₀=11010.0101₂:

Обратное преобразование двоичного числа в десятичное можно выполнить аналогично с тем различием, что делить и умножать нужно на 10 в двоичной системе, т.е. на 1010₂. Так 11010.0101₂=26.3125₁₀получается следующим образом:

Как видно, при использовании этого алгоритма цифры десятичного эквивалента двоичного числа выражаются первоначально в двоичной системе. Отводя для каждого десятичного разряда четыре двоичных разряда (тетраду), получим двоично-десятичную запись числа.

Проще всего переводятся в двоичные числа восьмеричные и шестнадцатеричные, основания которых представляет собой целые степени двойки, т.е. 8=2³ и 16=2⁴. Для этого достаточно каждый разряд восьмеричного числа представить тройкой (триадой), а шестнадцатеричного – четверкой (тетрадой) двоичных разрядов.

Например: 5327₈=101 011 010 111;

2DF9₁₆=0010 1101 1111 1001.

Обратный перевод двоичного числа в восьмеричное или шестнадцатеричное выполняется его разбиением на блоки (триады и тетрады) влево и вправо от разделительного символа. Недостающие разряды в крайнем левом и правом блоках дополняются нулями. Затем каждая триада заменяется восьмеричным, а каждая тетрада шестнадцатеричным числом.

Например: 1101010.11101=001 101 010. 111 010=152.72₈;

1101010.11101=0110 1010. 1110 100=5А.D8₁₆.

ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ

Обратный код n – разрядного числа N с основанием а дополняет его до максимально возможного значения аⁿ– 1 – N. При этом цифра каждого разряда обратного кода N₀ дополняет соответствующую цифру исходного числа N до наибольшей цифры а – 1 (для десятичных чисел – до 9). Дополнительный код числа N получается как разность N₀=aⁿ – N, так что он больше обратного кода на 1.

Сложение целых двоичных чисел с учетом знаков можно свести к обычному суммированию их дополнительных или обратных кодов. Эти коды для положительных чисел совпадают с прямым кодом, в котором один разряд (обычно старший) используется для кодирования знака числа (0 для положительного и 1 для отрицательного). Обратный код для отрицательного числа получается из прямого заменой 0 на 1 и 1 на 0 во всех разрядах, включая и знаковый. Чтобы выразить отрицательное число в дополнительном коде, достаточно к обратному коду прибавить 1.

Сложение в дополнительном коде осуществляется по правилам двоичной арифметики разряд за разрядом, включая знаковые разряды. Возможный перенос из знакового разряда игнорируется. При этом результат получается также в цифровом коде. Например:

₊(+9)₁₀= 01001 ₊(+7)₁₀=00111 ₊(-8)= 11000

(-5)₁₀= 11011 (-13)₁₀=10011 (-6)= 11010

(+4)₁₀=100100 (-6)₁₀=11010 (-14)=110010

Перенос игнорируется Перенос отсутствует Перенос игнорируется

Для алгебраического сложения можно воспользоваться и обратным кодом. Как и ранее, коды слагаемых, включая и знаковые разряды, суммируются как двоичные числа. Но перенос из старшего (знакового) разряда, если он возникает, не игнорируется, а прибавляется к младшему разряду суммы, которая также получается в обратном коде. Такой перенос называется круговым, а сложнее–циклическим.

Например:

(+15)₁₀=01111 (+7)₁₀=00111

(-5)₁₀=11010 (-11)₁₀=10100

Круговой ₊101001 (-4)₁₀=11011

перенос 1 Круговой перенос

(+10)₁₀=01010 отсутствует

Если оба слагаемых имеют одинаковые знаки, то может случиться переполнение, признаком которого служит различие знаков слагаемых и суммы. Другой признак основан на том, что переполнение происходит тогда и только тогда, когда при сложении имеет место один из переносов – в знаковый разряд или из знакового разряда, но не оба. В обратном коде этот признак следует применять до кругового переноса.

Вычитание в дополнительном и обратном кодах сводится к сложению путем замены знака (а значит, и кода) вычитаемого.

ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ

Для представления информации в десятичной системе счисления и выполнения операций над десятичными числами в цифровых устройствах используется двоично-десятичное кодирование, при котором каждая десятичная цифра представляется группой двоичных цифр. Число битов в таких группах строго фиксируется (их должно быть не менее четырех) с сохранением всех левых нулевых разрядов. В практике используется несколько разновидностей двоично-десятичных кодов (см. табл. 1.2), сохраняющих свое значение благодаря полезным специфическим особенностям.

Таблица 1.2

Десятичные цифры	Двоичные коды десятичных цифр
		С избытком 3	2 из 5

Наиболее естественным и популярным считается упоминавшийся код прямого замещения, в котором каждая цифра десятичного числа заменяется соответствующим четырехразрядным двоичным числом. Его другое название код 8421 отражает значение весовых множителей, приписываемых соответствующим битам в кодирующей группе, в связи с чем он называется также взвешенным кодом. Удобства этого кода проявляется при машинном переводе из десятичной системы в двоичную и обратно, а также при суммировании на обычных двоичных сумматорах благодаря его аддитивности (сумма кодов двух цифр представляется код суммы).

Избыточность тетрады, допускающей 16 кодовых комбинаций, позволяет создавать и другие варианты двоично-десятичных кодов с использованием четверки битов на десятичный разряд. Один из них код 2421 также взвешенный, но старший разряд имеет вес не 8, а 2. Его положительная особенность в том, что замена в кодирующей тетради нулей на единицы, а единиц на нули превращает каждую десятичную цифру х в 9–х, т. е. получается обратный код. Для превращения его в дополнительный код достаточно прибавить единицу. Коды с таким свойством называют самодополнительными. Они применяются при выполнении арифметических операций над десятичными числами в обратном или дополнительном коде.

Самодополнительным является код с избытком 3, который получается прибавлением 3₁₀=0011₂ к каждой цифре кода прямого замещения. Как и код 2421, он удобен для выполнения операций над десятичными числами. При этом легко определяется перенос, так как сумма двух слагаемых, каждое из которых берется с избытком 3, получится с избытком 6, что исключает лишние кодовые комбинации (для получения правильного кода суммы из полученного результата вычитается 3). Но этот код в отличие от кодов 8421 и 2412 не является взвешенным, вследствие чего мало удобен для преобразования чисел из одной системы в другую.

Используются также двоично-десятичные коды, в которых кодирующие тетради дополняются избыточными битами с тем, чтобы использовать эту избыточность для придания кодам цифических свойств, служащих для обнаружения ошибок и тем самым для повышения надежности вычислительных систем.

Так, в коде 2 из 5 каждая десятичная цифра представляется пятью разрядами, из которых два и только два содержат единицы. Если появится ошибка в одном из двоичных разрядов, т.е. если нуль превратится в единицу или единица превратится в нуль, то общее число единиц окажется больше или меньше двух, что можно обнаружить простым их подсчетом. Другой способ обнаружения одиночной ошибки основан на использовании бита, которым дополняется, какой либо код, для контроля четности. Значение дополнительного бита выбирается таким, таким чтобы общее число единиц в кодирующей группе всегда было четным или нечетным (в зависимости от принятого правила контроля). Рассмотренные способы обнаруживают одиночные ошибки, точнее, нечетное количество ошибок, но не реагируют на двойные ошибки и вообще четное количество ошибок. Существуют более сложные способы построения корректирующих кодов, используемых в технике связи, но в обычных вычислительных системах из-за громоздкости они не применяются.

Операции над десятичными числами выполняются с помощью несколько дополнительной двоичной арифметики. Так, при сложении двух чисел в коде прямого замещения 8421 необходимо добавить корректирующее слагаемое 6₁₀=0110₂ к каждой тетраде, в которой в процессе суммирования получена недопустимая цифра (1010, 1011, 1100, 1110 и 1111) или возник перенос в следующую тетраду.

Например:

₊38₁₀=0011 1000 ₊29₁₀=0010 1001

16₁₀=0001 0110 58₁₀=0101 1000

_{Коррекция +}0100 1110 _{Коррекция +}0100 1110

0000 0110 0000 0110

54₁₀=0101 0100 87₁₀=1000 0111

При вычитании чисел в коде 8421 коррекция сводится к вычитанию 6₁₀=0110₂ из каждой тетрады разности, которая потребовала заем. Например:

_–63₁₀=0110 0011

27₁₀=0010 0111

_{Коррекция –}0011 1100

0000 0110

36₁₀=0011 0110

Сложение и вычитание в десятичных чисел со знаками выполняются с использованием обратного, или дополнительного кодов аналогично соответствующим операциями, рассмотренным в разделе “Обратный и дополнительный коды”.