Задание №2 . Проверьте следующие равносильности двумя способами:

Задание №2 . Проверьте следующие равносильности двумя способами:

а) ;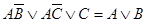

б) ;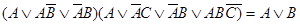

в) ;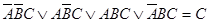

г) ;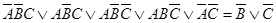

(максимальное количество баллов – 40)

Задание №3. Проверьте следующие равносильности, используя основные равносильности алгебры логики (предварительно упростив выражения, заключенные в скобки):

а) ;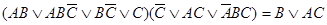

б) ;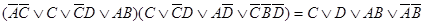

в) ;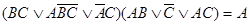

г) ;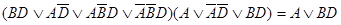

(максимальное количество баллов – 20)

Пример 3 б):

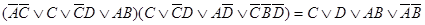
Ответ:

Первый способ проверки равносильностей - при помощи построения таблиц истинности ля левой и правой части формулы. Если истинностные значения в соответствующих столбцах совпадают при любых наборах значений составляющих простых суждений, то равносильность считается доказанной, в противном случае она не имеет места.

Составим таблицы истинности для левой и правой частей приведенной формулы (табл. 1, табл.2):

Таблица 1

А B

5+3

6+7

9+6+8

6+11+12

13*10

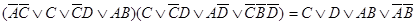
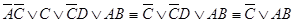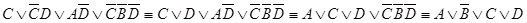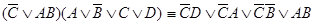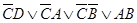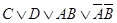Сравнивая столбец 14 табл. 1 и столбец 7 табл. 2, видим, что истинностные значения для левой и правой частей исходной формулы различны (не совпадают для одних и тех же наборов значений входящих в нее составляющих простых высказываний), значит, данная формула не являет равносильностью алгебры высказываний.

Таблица 2

А	B	C	D	А B	AB	3+4+5+6

Второй способ проверки равносильностей алгебры логики- преобразование исходной формулы на основании известных. Ранее доказанных основных равносильностей алгебры высказываний.

Используем для доказательства метод приведения левой части фрмулы к правой:

1) ;

2) ;

3) ;

4) ≠ .

Так как левая часть в результате равносильных преобразований не эквивалентна правой, можно сделать вывод, о том, что данная формула не является равносильностью алгебры высказываний.

Остальные задания: 2а), 2в), 2г) и задание №3 - выполнить самостоятельно.

В задании №3 все примеры нужно сделать только 2 способом, без таблиц.

Результаты каждый из вас высылает мне прикрепленным файлом в ЛК!

12 Следующая ⇒