
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение уравнений, сводящихся к квадратным уравнениям.
13.05. Решение уравнений, сводящихся к квадратным уравнениям.
Ход занятия: число, тема занятия.
1) Прочитайте параграф 23, рассмотрите решение примеров 1-3.
Решение уравнений, сводящихся к квадратным уравнениям, чаще всего выполняют методом замены переменной. Например, сегодня мы рассмотрим биквадратные уравнения, которые решают именно методом замены переменной.
Биквадратное уравнение – это уравнение вида ax4+bx2+c=0,
где х-переменная, а,b и с-некоторые числа.
2) Образцы решения уравнений запишите в тетрадь.
№775(1,5).
х4-5х2+4=0
(х2)2-5х2+4=0, х2=t
t2-5t+4=0
a=1,b=-5,c=4
D=b2-4ac
D=25-4∙1∙4=25-16=9
t1= 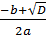 = = 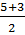 =4
t2= =4
t2= 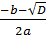 = = 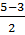 =1
х2=4 или х2=1
х1,2= =1
х2=4 или х2=1
х1,2= 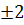 х3,4= х3,4= 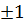 Ответ: х1,2=
Ответ: х1,2= 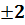 , х3,4= , х3,4= 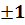 . .
| 4х4-9х2+2=0
4(х2)2-9х2+2=0, х2=t
4t2-9t+2=0
a=4,b=-9,c=2
D=b2-4ac
D=81-4∙4∙2=81-32=49
t1= 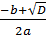 = = 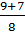 =2
t2= =2
t2= 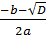 = = 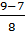 = = 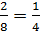 х2=2 или х2=
х2=2 или х2=  х1,2=
х1,2= 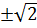 х3,4= х3,4= 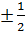 Ответ: х1,2=
Ответ: х1,2= 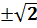 , х3,4= , х3,4= 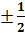 . .
|
№779(1).
(х+3)4-3(х+3)2-4=0
((х+3)2)2-3(х+3)2-4=0, (х+3)2=t
t2-3t-4=0
a=1,b=-3,c=-4 (можно использовать т.Виета для нахождения корней)
D=b2-4ac
D=9-4∙1∙(-4)=9+16=25
t1= 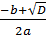 =
= 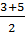 =4
=4
t2= 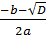 =
= 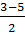 =
= 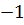
(х+3)2=4 или (х+3)2= 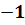 , (х+3)2
, (х+3)2 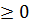
х+3=2 или х+3=-2 корней нет
х=2-3 х=-2-3
х=-1 х=-5
Ответ: х1=-1, х2=-5.
№781(1).
x-3 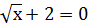
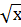 2-3
2-3 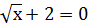 ,
, 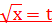
t2-3t+2=0, по т.Виета
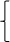 t1+t2=3
t1+t2=3
t1∙t2=2,
t1=2, t2=1
 или
или 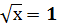 ,
,
х=4 х=1
Ответ: х=4, х=1.
Домашнее задание:#23, знать определение биквадратного уравнения,№776(3), 782(2), желающие №780(2).Работы скинуть в группу.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|