Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Алгебра. 9-б класс. 18.05.2020. 9-а класс.19.05.2020.
Тема урока: Степень с рациональным показателем. Простейшие задачи.

На данном уроке мы рассмотрим основные свойства степени с рациональным показателем и решим простейшие типовые задачи.

Рациональные числа, степень с рациональным показателем

Напомним, что такое множество рациональных чисел.

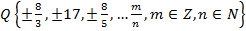– рациональные числа.

Каждая дробь может быть представлена в десятичном виде, например :

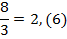
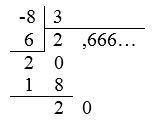
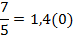
Итак, рациональное число может быть представлено как бесконечная десятичная дробь с периодом.

Напомним определение: для 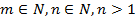выполняется равенство:

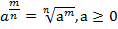
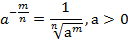
Например: 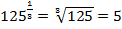; ; 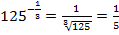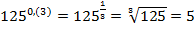(нужно перевести бесконечную периодическую дробь в обыкновенную).

Свойства степени с рациональным показателем, доказательства

Рассмотрим свойства степени с рациональным показателем, они аналогичны свойствам степени с натуральным показателем, здесь s и r – рациональные числа:

1. .

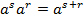Для того чтобы умножить степени с одинаковым основанием, нужно сложить их показатели, основание оставить без изменений.

2. .

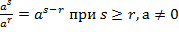Можно разделить степени с одинаковым основанием, для этого их показатели нужно вычесть, а основание оставить без изменений.

3. .

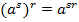Для того чтобы степень возвести в степень, нужно перемножить показатели степени, основание оставить без изменений.

4. .

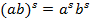При умножении степеней с одинаковым показателем, нужно перемножить основания и возвести результат в исходную степень.

5. .

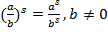Чтобы разделить степени с одинаковыми показателями, нужно разделить основания и возвести результат в исходную степень.

Вышеперечисленные свойства справедливы для любых рациональных показателей. Докажем первое свойство:

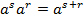
Доказательство:

s и r – рациональные числа, , ,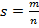

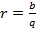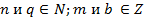
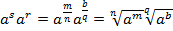Приведем корни к одинаковому показателю:

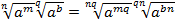Преобразуем полученное выражение согласно свойствам корня:

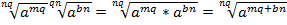По определению степени с рациональным показателем:

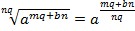Согласно свойствам степени:

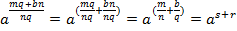Итак, получили:

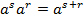Докажем третье свойство:

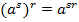
Доказательство:

s и r – рациональные числа, , , .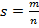

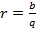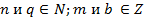Схема доказательства стандартная: от степеней перейти к корням, выполнить преобразования с корнями и вернуться к степеням.

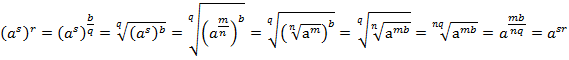
Остальные свойства доказываются аналогично.

Решение типовых задач

Перейдем к решению типовых задач.

Пример 1 – имеет ли смысл выражение:

а)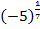

Ответ: нет.

б)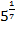

Ответ: да ( ).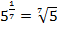

в)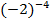

Ответ: да, т. к. -4 – целое число ( ).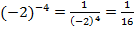

г)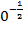

Ответ: нет.

Пример 2 – вычислить:

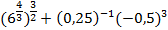
Рассмотрим слагаемые отдельно:

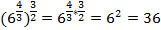
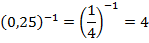
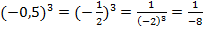Получаем:

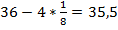Пример 3 – упростить выражение:

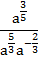
Упростим знаменатель:

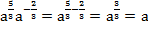Получаем:

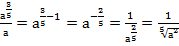Отметим, что обязательно в данном случае .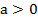

Пример 4 – упростить выражение:

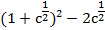
Возводим в квадрат двучлен:

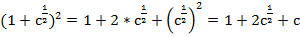Получили выражение:

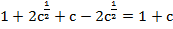В данной задаче могут быть поставлены дополнительные вопросы, например, допустимы ли отрицательные значения с. Ответ: нет, т. к. с имеет рациональный показатель степени и по определению является неотрицательным.

Пример 5 – упростить выражение:

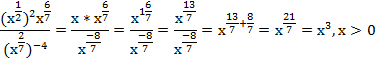
Комментарий: ограничение на х наложено в связи с тем, что он имеет отрицательный рациональный показатель степени.

Итак, мы рассмотрели свойства степеней с рациональным показателем. В дальнейшем мы перейдем к решению более сложных задач со степенями и радикалами.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Nado5.ru (Источник).

2. Интернет-портал Terver.ru (Источник).