
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задачи с прикладным характером.
| Предмет | Класс | Дата | |
| Алгебра и начала анализа | 11Б | 19.05.2020 | |
| Этапы урока | Деятельность | ||
| Добрый день! Сегодня мы решаем задачи с прикладным характером. По возможности поработаем в zoome, у кого такой возможности не будет, ниже прикрепляю задания для тренировки.
Задания для тренировки: | |||
Задачи с прикладным характером.
1.
Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью 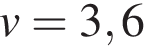 м/с под острым углом
м/с под острым углом 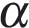 к рельсам. От толчка платформа начинает ехать со скоростью
к рельсам. От толчка платформа начинает ехать со скоростью 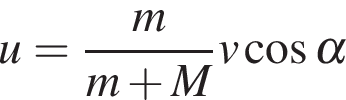 (м/с), где
(м/с), где  кг — масса скейтбордиста со скейтом, а
кг — масса скейтбордиста со скейтом, а 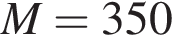 кг — масса платформы. Под каким максимальным углом
кг — масса платформы. Под каким максимальным углом 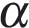 (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,3 м/с?
(в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,3 м/с?
2.
Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна 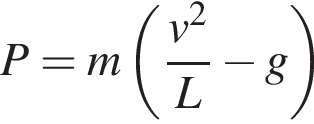 , где m — масса воды в килограммах, v — скорость движения ведeрка в м/с, L — длина верeвки в метрах, g — ускорение свободного падения (считайте
, где m — масса воды в килограммах, v — скорость движения ведeрка в м/с, L — длина верeвки в метрах, g — ускорение свободного падения (считайте  м/с
м/с  ). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 62,5 см? Ответ выразите в м/с.
). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 62,5 см? Ответ выразите в м/с.
3.
Уравнение процесса, в котором участвовал газ, записывается в виде 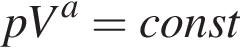 , где p (Па) — давление в газе, V — объeм газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение в 5 раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 25 раз?
, где p (Па) — давление в газе, V — объeм газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение в 5 раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 25 раз?
4.
Некоторая компания продает свою продукцию по цене  руб. за единицу, переменные затраты на производство одной единицы продукции составляют
руб. за единицу, переменные затраты на производство одной единицы продукции составляют  руб., постоянные расходы предприятия
руб., постоянные расходы предприятия  руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле
руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле 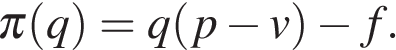 Определите месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 1 000 000 руб.
Определите месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 1 000 000 руб.
5.
Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной 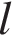 км с постоянным ускорением
км с постоянным ускорением 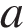 км/ч 2, вычисляется по формуле
км/ч 2, вычисляется по формуле  Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
6.
Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле 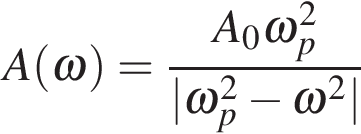 , где
, где 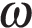 — частота вынуждающей силы (в
— частота вынуждающей силы (в 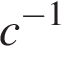 ),
), 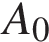 — постоянный параметр,
— постоянный параметр, 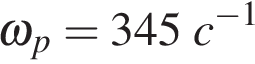 — резонансная частота. Найдите максимальную частоту
— резонансная частота. Найдите максимальную частоту 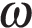 , меньшую резонансной, для которой амплитуда колебаний превосходит величину
, меньшую резонансной, для которой амплитуда колебаний превосходит величину 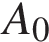 не более чем на
не более чем на 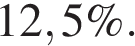 Ответ выразите в
Ответ выразите в 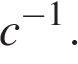
7.
В телевизоре ёмкость высоковольтного конденсатора 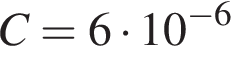 Ф. Параллельно с конденсатором подключeн резистор с сопротивлением
Ф. Параллельно с конденсатором подключeн резистор с сопротивлением 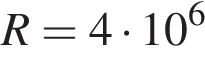 Ом. Во время работы телевизора напряжение на конденсаторе
Ом. Во время работы телевизора напряжение на конденсаторе 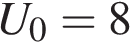 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением
кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением 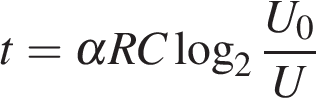 (с), где
(с), где 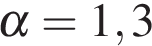 — постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло 62,4 с. Ответ дайте в киловольтах.
— постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло 62,4 с. Ответ дайте в киловольтах.
8.
 На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
Введём систему координат: ось Oy направим вертикально вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано на рисунке.
В этой системе координат линия, по которой провисает цепь моста, имеет уравнение 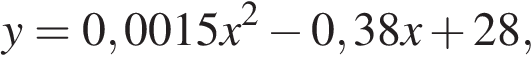 где x и y измеряются в метрах. Найдите длину ванты, расположенной в 40 метрах от пилона. Ответ дайте в метрах.
где x и y измеряются в метрах. Найдите длину ванты, расположенной в 40 метрах от пилона. Ответ дайте в метрах.
9.
Зависимость объeма спроса 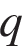 (единиц в месяц) на продукцию предприятия – монополиста от цены
(единиц в месяц) на продукцию предприятия – монополиста от цены 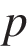 (тыс. руб.) задаeтся формулой
(тыс. руб.) задаeтся формулой 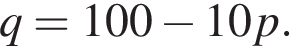 Выручка предприятия за месяц
Выручка предприятия за месяц  (в тыс. руб.) вычисляется по формуле
(в тыс. руб.) вычисляется по формуле  Определите наибольшую цену
Определите наибольшую цену 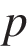 , при которой месячная выручка
, при которой месячная выручка 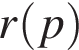 составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.
составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.
10.
Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому 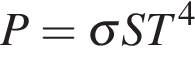
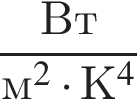 , где
, где 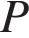 — мощность излучения звезды (в Ваттах),
— мощность излучения звезды (в Ваттах), 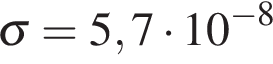 — постоянная,
— постоянная, 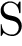 м
м  — площадь поверхности звезды (в квадратных метрах), а
— площадь поверхности звезды (в квадратных метрах), а 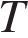 — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна
— температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна 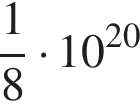 м
м  , а мощность её излучения равна
, а мощность её излучения равна 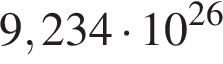 Вт. Найдите температуру этой звезды в Кельвинах.
Вт. Найдите температуру этой звезды в Кельвинах.
Домашнее задание: не задано