Правило произведения. Размещения с повторениями.

Правило произведения. Размещения с повторениями.

Область математики, в которой изучаются вопросы подсчёта комбинаций (соединений), составленных из заданных объектов и подчинённых тем или иным условиям, называется комбинаторикой.

В основной школе решались элементарные комбинаторные задачи, связанные с составлением и подсчётом различных соединений (комбинаций) из имеющихся элементов. Было сформулировано правило произведения, упрощающее подсчёт числа определённых соединений.

Правило произведения.Если существует n вариантов выбора первого элемента и для каждого из них имеется m вариантов выбора второго элемента, то существует 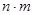различных пар с выбранными первыми и вторыми элементами.

Задача 1.Сколько различных двузначных чисел можно записать с помощью цифр 0, 2, 4, 6, 8?

Решение.

В качестве первой цифры может быть выбрана любая из цифр 2, 4, 6, 8 (n = 4). Второй цифрой может служить любая из данных цифр 0, 2, 4, 6, 8 (т = 5).

Согласно правилу произведения число всевозможных двузначных чисел, составленных из предложенных цифр, равно .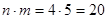

Ответ: 20.

Задача 2. В школьной олимпиаде по математике победителями оказались 3 человека, в олимпиаде по физике – 2 человека, в олимпиаде по химии – 4 человека. На районные олимпиады по математике, физике и химии школа должна направить по одному учащемуся из числа победителей школьных туров по трём предметам. Сколькими способами можно это сделать?

Решение.

Применив дважды правило произведения имеем: ; .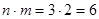

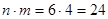Или имеем сразу: .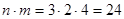

Ответ: 24.

Задача 3. Сколько различных четырёхбуквенных слов можно записать с помощью букв «м» и «а»? (словом в комбинаторике называют любую последовательность букв).

Решение.

Каждую из четырёх букв составляемого слова последовательно выбирается из имеющихся двухбукв. Применив трижды правило произведения, найдём число составляемых четырёхзначных слов:

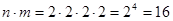Ответ: 16.

Соединения, содержащие п элементов, выбираемых их элементов т различных видов, и отличающиеся одно от другого либо составом, либо порядком следования в них элементов, называют размещениями с повторениями из т по п.

Число всевозможных размещений с повторениями из т по п обозначают 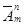и читают: «Число размещений с повторениями из эм по эн» или «А с чертой из эм по эн».

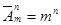
Задача 4. Сколько различных четырёхбуквенных слов можно записать с помощью букв «м» и «а»? (словом в комбинаторике называют любую последовательность букв).

Решение.

;

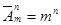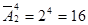Ответ: 16.

Задача 5. В двоичной системе счисления, применяемой в компьютерах, используют два символа: 0 и 1. В некотором компьютере каждое слово записывается в памяти с помощью этих символов в 16 пронумерованных разрядах. Сколько различных машинных слов можно записать в этих разрядах?

Решение.

В каждом из 16 разрядов может стоять один из двух символов. Очевидно, что число различных машинных слов равно:

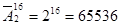Ответ: 65536.

Домашнее задание.

№ 409.Сколько разных трёхзначных чисел, не имеющих одинаковых цифр, можно записать с помощью цифр: 1) 1, 2 и 3; 2) 1, 2, 3 и 4?

№ 410.Сколько разных трёхзначных чисел можно записать с помощью цифр: 1) 6, 7 и 8; 2) 6, 7, 8 и 9?

№ 411.Сколько разных двузначных чисел можно записать, используя цифры 1, 2, 3 и 4?