
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Группа – ЭТ-19 11.04.2020
Группа – ЭТ-19 11.04.2020
Дисциплина – Математика (1 пара)
Тема: Практическая работа № 22 по теме «Объемы и площади поверхностей многогранников и тел вращения».
Выполнить практическую работу в тетради.
Вариант выбираете согласно номеру по списку.
Фото выполненной работы отправить по окончанию пары до 11.00 только по ссылке https://vk.com/topic-193913663_41367162
| 1 | Абдулов Тимур Миргейизович |
| Амахин Сергей Юрьевич | |
| Ахмедов Тимур Мовлидинович | |
| Гаррыбаев Александр Дмитриевич | |
| Капитула Павел Алексеевич | |
| Куликов Игорь Витальевич | |
| Левин Максим Сергеевич | |
| Лозовой Денис Викторович | |
| Маслов Илья Александрович | |
| Матвеев Валерий Романович | |
| Мельников Владимир Максимович | |
| Ненахов Данила Русланович | |
| Никонов Роман Павлович | |
| Паращук Ярослав Олегович | |
| Петровых Наталья Викторовна | |
| Руссу Дмитрий Дмитриевич | |
| Савинов Антон Васильевич | |
| Селиверстов Павел Викторович | |
| Соколов Валерий Вячеславович | |
| Таранов Денис Николаевич | |
| Чукин Алексей Иванович | |
| Чуркина Эльвира Дмитриевна | |
| Шиловский Даниил Николаевич |
Вариант 1.
1. По боковому ребру 8 см и стороне основания 2 см найти объем и площадь полной поверхности правильной треугольной пирамиды.
2. Диагональ осевого сечения цилиндра равна 26 см, высота цилиндра равна 24 см. Найти объем и площадь полной поверхности цилиндра.
3. В конус вписан шар объемом 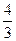 π см3. Найдите объем и площадь полной поверхности конуса, если его высота 3см.
π см3. Найдите объем и площадь полной поверхности конуса, если его высота 3см.
Вариант 2.
1. По стороне основания 2 см и высоте 8 см найти объем и площадь полной поверхности правильной треугольной пирамиды.
2. Радиус основания конуса 5 см, его высота 12 см. Найти объем, площадь полной поверхности конуса и угол наклона образующей к плоскости основания.
3. Объем цилиндра равен 96π см3, площадь его осевого сечения – 48 см2. Найдите объем сферы, описанной около цилиндра.
Вариант 3.
1. По стороне основания 4 см и боковому ребру 10 см найти объем и площадь полной поверхности правильной четырехугольной пирамиды.
2. Высота конуса равна 6 см. Угол между высотой и образующей равен 300. Найти объем и площадь полной поверхности конуса.
3.Радиус сферы, описанной около цилиндра, равен 12 см и равен высоте цилиндра. Найдите объем и площадь полной поверхности цилиндра.
Вариант 4.
1. Стороны основания прямоугольного параллелепипеда равны 6 см и 8 см, а площадь диагонального сечения 180 см2. Найти объем и площадь полной поверхности.
2. Радиус основания конуса равен 4 см и составляет с образующей угол в 300. Найти объем и площадь полной поверхности конуса.
3.Объем цилиндра равен V. Найдите объем правильной четырехугольной призмы, описанной около цилиндра.
Вариант 5.
1. Основанием прямого параллелепипеда служит ромб с диагоналями 12 см и 16 см, диагональ боковой грани равна 26 см. Найти объем и площадь полной поверхности параллелепипеда.
2. Образующая конуса наклонена к плоскости основания под углом в 600. Радиус основания 6 см. Найти объем и площадь полной поверхности конуса.
3.В правильную четырехугольную пирамиду вписан шар объемом 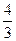 π см3. Найдите объем пирамиды, если ее высота 5 см.
π см3. Найдите объем пирамиды, если ее высота 5 см.
Вариант 6.
1. В правильной треугольной пирамиде боковое ребро равно 20 см и образует с плоскостью основания угол 600. Найти объем и площадь полной поверхности .
2. Площадь полной поверхности цилиндра равна 125π см2. Найдите площадь его боковой поверхности и объем, если радиус основания 5 см.
3. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение объемов сферы и конуса.
Вариант 7.
1. Сторона основания правильной четырехугольной пирамиды 8 см, высота – 3 см. Найти объем и площадь полной поверхности пирамиды.
2. Высота конуса равна 6 см. Угол между высотой и образующей равен 300. Найти объем и площадь полной поверхности конуса.
3.Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов шара и цилиндра.
Вариант 8.
1. Сторона основания правильной треугольной пирамиды 8 см, высота – 3 см. Найдите объем и площадь полной поверхности.
2. Сечение шара плоскостью, отстоящей от его центра на расстоянии 6 см, имеет радиус 8 см. Найти объем шара и площадь полной поверхности сферы .
3.Радиус основания конуса равен 4 см, а его высота 10 см. в конус вписан цилиндр так, что его верхнее основание касается боковой поверхности конуса, а нижнее лежит в плоскости основания. Найдите объем цилиндра, если его осевое сечение – квадрат.
Вариант 9.
1. В правильной треугольной пирамиде боковое ребро равно 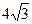 см и образует с плоскостью основания угол в 600. Найти объем и площадь полной поверхности пирамиды.
см и образует с плоскостью основания угол в 600. Найти объем и площадь полной поверхности пирамиды.
2. Образующая конуса равна 12 см, а угол между нею и плоскостью основания равен 300. Найти объем и площадь полной поверхности конуса.
3. Дан куб с ребром 2 см. Найдите объем шара, описанного около куба.
Вариант 10.
1. В правильной треугольной пирамиде сторона основания равна 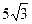 см, а боковое ребро – 13 см. Найдите объем и площадь полной поверхности пирамиды.
см, а боковое ребро – 13 см. Найдите объем и площадь полной поверхности пирамиды.
2. Образующая конуса равна 18 см, а угол при вершине осевого сечения равен 600. Найти объем и площадь полной поверхности конуса.
3. Найдите объем шара, вписанного в куб с ребром 2 см.
Вариант 11.
1. Сторона основания правильной четырехугольной пирамиды 6 см, а боковая грань наклонена к плоскости основания под углом 450. Найти объем и площадь полной поверхности пирамиды.
2. Образующая конуса наклонена к плоскости основания под углом 30°, его высота 12 см. Найти объем и площадь полной поверхности конуса.
3. Около правильной четырехугольной призмы со стороной основания 2 см и боковым ребром 1 см описан шар. Найдите объем шара.
Вариант 12.
1. В правильной треугольной пирамиде сторона основания равна 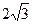 см, а боковая грань наклонена к основанию под углом 300. Найти объем и площадь полной поверхности пирамиды.
см, а боковая грань наклонена к основанию под углом 300. Найти объем и площадь полной поверхности пирамиды.
2. Образующая конуса равна 14 см, а его радиус – 7 см. Найти угол между образующей и основанием, объем и площадь полной поверхности конуса.
3.Стороны основания прямоугольного параллелепипеда 3 см и 4 см, боковое ребро 4 см. найдите объем описанного шара.
Вариант 13.
1. Основание прямой призмы – треугольник со сторонами 4 см и 8 см и образуют угол 300, ее боковое ребро равно 4 см. Найти объем и площадь полной поверхности призмы.
2.Площадь основания цилиндра равна 16π см2, площадь его осевого сечения равна 24 см2. Найти объем и площадь полной поверхности цилиндра.
3.В конус вписан шар. Найдите объем шара, если образующая конуса равна 12 см и наклонена к плоскости основания под углом 60º.
Вариант 14.
1. Сторона основания правильной четырехугольной пирамиды равна 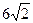 см, а боковое ребро 10 см. Найдите объем и площадь полной поверхности пирамиды.
см, а боковое ребро 10 см. Найдите объем и площадь полной поверхности пирамиды.
2. Высота конуса равна 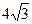 см, а угол при вершине осевого сечения равен
см, а угол при вершине осевого сечения равен 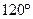 . Найдите объем и площадь полной поверхности конуса.
. Найдите объем и площадь полной поверхности конуса.
3.Объем цилиндра равен 96π см3. Площадь его осевого сечения 48 см2. Найдите объем шара, описанного около цилиндра.
Вариант 15.
1. В прямой треугольной призме стороны оснований равны 13 см, 20 см и 21 см, а высота призмы равна 25 см. Вычислить объем и площадь полной поверхности призмы.
2. Чему равен объем и площадь полной поверхности шарового сектора, если радиус окружности его основания 60 см, а радиус шара 75 см?
3. В конус, высота которого  см, а образующая составляет угол 60º с плоскостью основания, вписан шар. Найдите объем шара.
см, а образующая составляет угол 60º с плоскостью основания, вписан шар. Найдите объем шара.
Вариант 16.
1. В правильной треугольной пирамиде сторона основания равна  см, а высота 3 см. Найти объем и площадь полной поверхности пирамиды.
см, а высота 3 см. Найти объем и площадь полной поверхности пирамиды.
2. Диагональ осевого сечения цилиндра равна 8 дм и составляет с образующей угол 60º. Найдите объем и площадь полной поверхности цилиндра.
3. В конус, высота которого 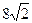 см, а радиус основания 4 см, вписан куб так. Что четыре вершины принадлежат основанию конуса, а другие четыре – боковой поверхности. Найдите объем куба.
см, а радиус основания 4 см, вписан куб так. Что четыре вершины принадлежат основанию конуса, а другие четыре – боковой поверхности. Найдите объем куба.
Вариант 17.
1. По боковому ребру 8 см и стороне основания 2 см найти объем и площадь полной поверхности правильной треугольной пирамиды.
2. Радиус основания конуса 5 см, его высота 12 см. Найти объем, площадь полной поверхности конуса и угол наклона образующей к плоскости основания.
3.Радиус сферы, описанной около цилиндра, равен 12 см и равен высоте цилиндра. Найдите объем и площадь полной поверхности цилиндра.
Вариант 18.
1. Стороны основания прямоугольного параллелепипеда равны 6 см и 8 см, а площадь диагонального сечения 180 см2. Найти объем и площадь полной поверхности.
2. Образующая конуса наклонена к плоскости основания под углом в 600. Радиус основания 6 см. Найти объем и площадь полной поверхности конуса.
3. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение объемов сферы и конуса.
Вариант 19.
1. Сторона основания правильной четырехугольной пирамиды 8 см, высота – 3 см. Найти объем и площадь полной поверхности пирамиды.
2. Сечение шара плоскостью, отстоящей от его центра на расстоянии 6 см, имеет радиус 8 см. Найти объем шара и площадь полной поверхности сферы .
3. Дан куб с ребром 2 см. Найдите объем шара, описанного около куба.
Вариант 20.
1. В правильной треугольной пирамиде сторона основания равна 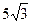 см, а боковое ребро – 13 см. Найдите объем и площадь полной поверхности пирамиды.
см, а боковое ребро – 13 см. Найдите объем и площадь полной поверхности пирамиды.
2. Образующая конуса наклонена к плоскости основания под углом 30°, его высота 12 см. Найти объем и площадь полной поверхности конуса.
3.Стороны основания прямоугольного параллелепипеда 3 см и 4 см, боковое ребро 4 см. найдите объем описанного шара.
Вариант 21.
1. Основание прямой призмы – треугольник со сторонами 4 см и 8 см и образуют угол 300, ее боковое ребро равно 4 см. Найти объем и площадь полной поверхности призмы.
2. Высота конуса равна 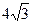 см, а угол при вершине осевого сечения равен
см, а угол при вершине осевого сечения равен 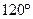 . Найдите объем и площадь полной поверхности конуса.
. Найдите объем и площадь полной поверхности конуса.
3. В конус, высота которого 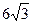 см, а образующая составляет угол 60º с плоскостью основания, вписан шар. Найдите объем шара.
см, а образующая составляет угол 60º с плоскостью основания, вписан шар. Найдите объем шара.
Вариант 21.
1. По стороне основания 4 см и боковому ребру 10 см найти объем и площадь полной поверхности правильной четырехугольной пирамиды.
2. Радиус основания конуса равен 4 см и составляет с образующей угол в 300. Найти объем и площадь полной поверхности конуса.
3.Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов шара и цилиндра.
Вариант 22.
1. Сторона основания правильной треугольной пирамиды 8 см, высота – 3 см. Найдите объем и площадь полной поверхности.
2. Образующая конуса равна 12 см, а угол между нею и плоскостью основания равен 300. Найти объем и площадь полной поверхности конуса.
3. Найдите объем шара, вписанного в куб с ребром 2 см.
Вариант 23.
1. В правильной треугольной пирамиде сторона основания равна 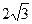 см, а боковая грань наклонена к основанию под углом 300. Найти объем и площадь полной поверхности пирамиды.
см, а боковая грань наклонена к основанию под углом 300. Найти объем и площадь полной поверхности пирамиды.
2. Чему равен объем и площадь полной поверхности шарового сектора, если радиус окружности его основания 60 см, а радиус шара 75 см?
3.Объем цилиндра равен 96π см3. Площадь его осевого сечения 48 см2. Найдите объем шара, описанного около цилиндра.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|