Сила тяжести

Закон Всемирного тяготения

Открыт Ньютоном в 1667 году на основе анализа движения планет (з-ны Кеплера) и, в частности, Луны.

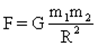Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.

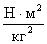Сила направлена вдоль прямой, соединяющей тела.

G - постоянная всемирного тяготения (гравитационная постоянная). G=6,67^.10^-11

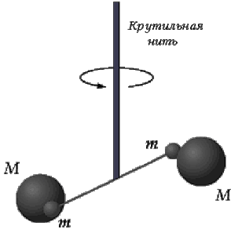Опыт Кавендиша (определение гравитационной постоянной)

Физический смысл гравитационной постоянной:

гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами

массой по 1 кг каждое, находящимися на расстоянии

1 м друг от друга.

Закон справедлив для:

1. Однородных шаров.

2. Для материальных точек.

3. Тело в форме большого шара и малого тела произвольной формы.

Сила тяжести

Сила тяжести – сила притяжения тел к Земле (планете)

- из закона Всемирного тяготения. (где M- масса планеты, m - масса тела, R - расстояние до центра планеты).

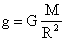F = mg - сила тяжести из второго закона Ньютона (где m - масса тела, g - ускорение силы тяжести).

Ускорение силы тяжести не зависит от массы тела (опыты Галилея)

g = 9,8 м/c²на поверхности Земли

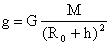Если обозначить R₀ радиус планеты, а h- расстояние до тела от поверхности планеты, то:

Ускорение силы тяжести зависит:

Массы планеты.
Радиуса планеты.
От высоты над поверхностью планеты.
От географической широты (на полюсах - 9,83 м/с². на экваторе - 9,79 м/с².

5. От залежей полезных ископаемых.

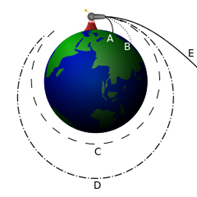Первая космическая скорость - минимальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.

По 2 закону Ньютона ma = GMm/R²

где {\displaystyle m}m — масса объекта,

{\displaystyle a}a — его ускорение, M{\displaystyle M} — масса планеты,

{\displaystyle R}R — радиус орбиты

При движении тела по окружности с постоянной по модулю скоростью {\displaystyle v}υ его ускорение а равно центростремительному ускорению а = υ²/R

m υ²/R= GMm/R²;

первая космическая скорость υ₁ = √GM/R

Подставив M = 6·10²⁴ кг, R₀ = 6400 км, получим υ₁≈ 7,9 км/с

Радиус орбиты складывается из радиуса планеты {\displaystyle R_{0}}R₀ и высоты над её поверхностью {\displaystyle h}h. Соответственно, последнее равенство можно представить в виде

υ₁ = √GM/(R₀+h)

Период обращения спутника по круговой орбите равен: Т=2πR/υ=2π√R/GM

При удалении спутника от центра Земли в 42 200 км период обращения становится равным 24 часа, то есть времени обращения Земли вокруг своей оси. Если запустить на круговую орбиту спутник на такой высоте в сторону вращения Земли в плоскости экватора, то он будет висеть над одним и тем же местом поверхности Земли на высоте 35 800 км (геостационарная орбита)

С увеличением высоты орбиты первая космическая скорость уменьшается. Так, на высоте 100 км над поверхностью Земли она равна 7 844 м/с, а на высоте 300 км — 7 726 м/с.

Другое выражение первой космической скорости имеет вид:

υ₁ = √gR{\displaystyle v_{1}={\sqrt {gR}}},

где {\displaystyle g}g - ускорение свободного падения на расстоянии {\displaystyle R}R от центра Земли.

Вторая космическая скорость - наименьшая скорость, которую необходимо придать объекту, чтобы он преодолел гравитационное притяжение планеты и покинул замкнутую орбиту вокруг нее (стало двигаться по параболе). Для Земли вторая космическая скорость равна 11,186 км/с.

Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.

Запишем затем закон сохранения энергии m υ₂²/2 - GMm/R =0, R=r+h

где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, r — радиус планеты, h - высота над поверхностью планеты, G — гравитационная постоянная, υ₂ — вторая космическая скорость.

Решая это уравнение относительно υ₂, получим υ₂ = √2GM/R

Между первой и второй космическими скоростями существует простое соотношение:

υ₂ = √2 υ₁ {\displaystyle v_{2}={\sqrt {2}}v_{1}.} {\displaystyle {\frac {v^{2}}{R}}\ .}