ГЕОМЕТРИЯ. Тема урока: Анализ контрольной работы. Решение задач практического содержания.. КЛАССНАЯ РАБОТА. Задание 3. Задача 7

06.05.2020

ГЕОМЕТРИЯ

8 класс

(2ч.)

Тема урока: Анализ контрольной работы. Решение задач практического содержания.

Цель: -проанализировать контрольную работу;

- сделать работу над ошибками, допущенными при выполнении контрольной работы;

-усовершенствовать навыки решения задач;

-устранить пробелы в знаниях по теме;

-развивать навыки рефлексии, самоанализа и критического мышления;

КЛАССНАЯ РАБОТА

1. Запишите в тетрадь число и тему урока.

2. Давайте проанализируем контрольную работу.

Наибольшие затруднения вызвало решение задачи 3 из тестовой части, задачи 7 из 2 части и задачи 8 из 3 части.

Задание 3

Треугольник АВС вписан в окружность. Точки А, В, и С делят окружность на дуги в отношении 2:3:4. Найти больший угол треугольника АВС

1) 160°. 2)120°.

3)100°. 4)80°.

Пояснения:

Нужно было вспомнить, что градусная мера дуги окружности -это величина соответствующего ей центрального угла. Сумма всех центральных углов окружности 360° Точки А, В, и С делят окружность на дуги в отношении 2:3:4 , всего 9 частей. Каждая часть соответствует ? градусов, соответственно самая большая дуга будет равна 4 умножить на ? градусов одной части. Нашли градусную меру самой большой дуги окружности и соответствующего ей центрального угла. Самый больший угол треугольника АВС- вписанный угол в окружность и по теореме о вписанном угле измеряется половиной дуги, на которую опирается, соответственно половиной самой большой дуги окружности, которую мы нашли.

Задача 7

Сторона MP треугольника MKP равна 24. Серединные перпендикуляры к сторонам этого треугольника пересекаются в точке D, причём DP = 13. Найдите расстояние от точки D до стороны MP.

Пояснения:

В этой задаче важную роль играет рисунок. Обозначим точку пересечения серединного перпендикуляра и стороны МР как А. Из построения видно, что треугольник АDР - прямоугольный и АР=1/2МР по свойству серединного перпендикуляра. Расстояние от точки D до стороны MP-катет треугольника АDР у которого известна гипотенуза и другой катет. По теореме Пифагора легко найти искомое расстояние.

Задача 8

Одна из сторон треугольника равна 13 см, а другая сторона точкой касания вписанной окружности делится на отрезки 6 см и 8 см, считая от известной стороны. Найдите радиус окружности, вписанной в этот треугольник.

Пояснения:

В этой задаче нужно вспомнить свойства отрезков касательной, проведенных из одной точки. Используя это свойство можно найти все стороны искомого треугольника и по формуле Герона вычислить площадь этого треугольника. По свойству вписанной окружности - площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности. Из этого свойства, зная площадь и полупериметр легко найти радиус вписанной в него окружности.

3. Используя пояснения – сделай работу над ошибками. Запиши в тетрадь решение неверно выполненных задач правильно. Проанализируй свою контрольную работу. Определи темы и задачи, которые вызывают затруднения.

4. Для закрепления реши предложенные задачи:

Задача 1

Серединные перпендикуляры к сторонам остроугольного треугольника ABC пересекаются в точке O так, что расстояние от этой точки до стороны AC равно 8. Найдите длину отрезка CO, если AC = 30°.

Задача 2

В прямоугольный треугольник вписана окружность радиуса 2 см. Точка касания делит гипотенузу на два отрезка длиной 5 см и 3 см. Найдите периметр треугольника. Ответ дайте в сантиметрах.

5. Разомнись и потанцуй под хорошую музыку

https://zvideox.ru/watch/Ksli61pE2SI/fizminutka-tanets/

6. Геометрия – это не просто наука о свойствах треугольников, параллелограммов, окружностей. Геометрия – это целый мир, который окружает нас с самого рождения. Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.

На уроке рассмотрим красивые задачи, решить которые, помогут знания по геометрии, которые вы получили в 8 классе.

Задача 1. Измерение высоты дерева

Для того, чтобы измерить высоту дерева BD, приготовили прямоугольный треугольник АВ1C1 с углом А = 45о и, держа его вертикально, отошли на такое расстояние, при котором, глядя вдоль гипотенузы АВ1, увидели верхушку дерева В. Какова высота дерева, если расстояние
АС = 5,6м, а высота человека 1,7м?

Дано:

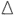АВ1С1,
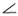С = 90о,
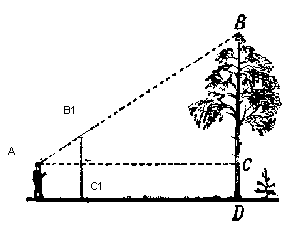
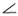А = 45о.
АС = 5,6м
h человека = 1,7м.

Задача 2. Земля как на ладони, когда ты в небе на воздушном шаре

Как далеко видно с воздушного шара, поднявшегося на высоту 4 км над Землей (радиус Земли примерно равен 6370 км)?

Решение:

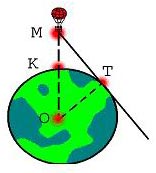
1. По теореме о касательной к окружности, касательная перпендикулярна радиусу, проведенному в точку касания, то есть OTM = 90о.
2. MO = 6370 + 4 = 6374 км,
3. тогда по теореме Пифагора:

MT 2 + OT 2 = MO 2
MT 2 = MO 2 – OT 2

MT = 112,9 км

Ответ: 112,9 км

ДОМАШНЕЕ ЗАДАНИЕ

1.Творческое задание: придумай, составь и реши задачу по геометрии практического содержания на любую из пройденных тем. Текст и решение пришли мне.

Скриншоты и фото заданий присылайте на

e-mail chetverik-1967@mail.ru

https://vk.com/wall-193681717_1