Формула Бернулли. Решение.. Решение.

Формула Бернулли

В курсе теории вероятностей обосновывается следующее утверждение.

Если произведено п независимых испытаний, то вероятность события В, состоящего в том, что в первом испытании произойдёт событие А₁, во втором – событие А₂, …, в п-м – событие А_п, равна произведению вероятностей событий А₁, А₂, …, А_п.

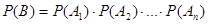Задача 1.Стрелок поражает мишень при каждом выстреле с вероятностью 0,8. Какова вероятность того, что мишень будет поражена лишь при первом и при третьем выстрелах, если стрелок выстрелит по мишени 3 раза?

Решение.

А – попадание стрелком по мишени при одном выстреле. .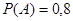

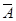- промах. .

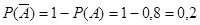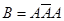- попадание в цель при первом и третьем выстрелах.

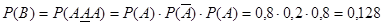Ответ: 0,128.

Задача.Вычислить вероятность события В, заключающегося в том, что при п независимых испытаниях событие А произойдёт ровно k раз.

Вероятность события В принято обозначать P_n(k), подчёркивая тем самым что рассматривается вероятность события, наступившего ровно k раз в серии из п однотипных испытаний.

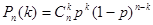где ,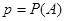

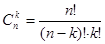
Данная формула называется формулой Бернулли.

Задача 2. Игральный кубик бросают 4 раза. Какова вероятность того, что в этой серии испытаний 5 очков появится ровно 3 раза?

Решение.

А – появление 5 очков в одном испытании.

Событие А в каждом из четырёх независимых испытаний может произойти, а может и не произойти.

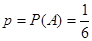Тогда по формуле Бернулли .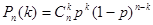

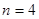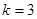
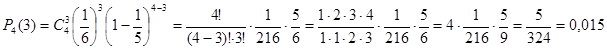Ответ: 0,015.

Домашнее задание.

№ 556. Одновременно бросают две игральные кости. Найти вероятность того, что сумма выпавших очков равна 8.

№ 560. По мишени стреляют 2 раза. Вероятность попадания в мишень при первом выстреле равна 0,8, при втором – 0,9. Какова вероятность того, что мишень не будет поражена ни одним выстрелом?