Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Алгебра. 7 класс. 19.05.2020.
Тема урока: Повторение. Степень с натуральным показателем и её свойства.

На данном уроке мы вспомним основные определения и свойства степени с натуральным показателем, кроме того, вспомним все основные теоремы и решим различные примеры, чтобы закрепить данную тему.

Основные определения

Вспомним основные определения:

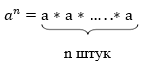– степень с натуральным показателем, здесь а – основание степени, n – показатель степени.

Кроме того, напомним, что:

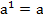и ;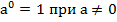

Символ 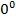, как и символ 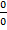не имеет смысла.

Все одночлены, многочлены и основные операции с ними основаны на степенях и действиях со степенями, которые мы сейчас вспомним:

Основные теоремы о степенях с одинаковым основанием

Основные теоремы о действиях со степенями:

;

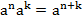Для того чтобы умножить степени с одинаковым основанием, нужно сложить их показатели, основание оставить тем же самым.

;

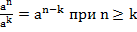Можно разделить степени с одинаковым основанием, для этого их показатели нужно вычесть, а основание оставить тем же самым;

Пример 1: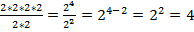

;

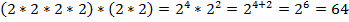
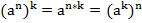Для того чтобы степень возвести в степень, нужно перемножить показатели степени, основание оставить без изменений.

Основные правила работы со степенями с одинаковым показателем

Мы вспомнили основные правила работы со степенями с одинаковым основанием. В качестве примеров выведем еще несколько правил:

Пример 2: 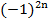– возвести минус единицу в четную степень; 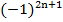– возвести минус единицу в нечетную степень;

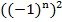– при возведении в квадрат любое число станет положительным, единица в любой степени равна единице, таким образом, независимо от значения 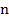выражение 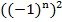равно единице.

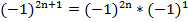
В предыдущем примере мы показали, что выражение 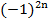всегда равно единице. Получаем:

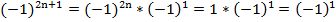
Минус единица в первой степени равна сама себе, получаем:

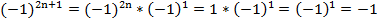
Рассмотрим теперь правила обращения со степенями с одинаковым показателем:

;

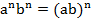При умножении степеней с одинаковыми показателями, нужно перемножить основания и возвести результат в исходную степень;

, ;

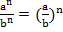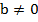Чтобы разделить степени с одинаковыми показателями, нужно разделить основания и возвести результат в исходную степень;

Пример 3:

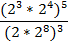
Итак, в числителе и знаменателе перемножим степени с одинаковым основанием:

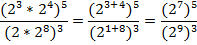
Возведем в числителе и знаменателе степень в степень:

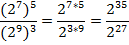
Выполним деление степеней с одинаковым основанием:

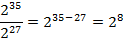
Чтобы получить результат, выполним некоторые преобразования:

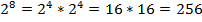
Решение вычислительных примеров

Пример 4: вычислить:

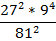
Чтобы решить данный пример, все основания степеней нужно привести к самому простому:

, ,

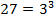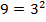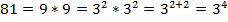
Итак, получаем:

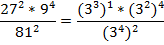
Выполним возведение степени в степень:

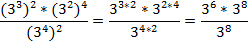
Выполним сокращение дроби:

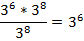
Вычислим:

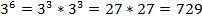
Решение других типовых задач

Пример 5: запишите в виде степени с показателем 2:

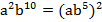
Для того чтобы получить ответ, мы исходные показатели степеней разделили на 2.

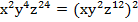
Пример 6: заменить звездочку таким выражением, чтобы получилось верное равенство:

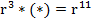
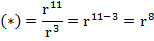
Получаем выражение:

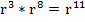– равенство верно

Пример 7: решить уравнение:

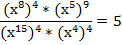
Будем постепенно выполнять действия со степенями в левой части:

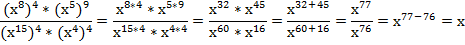
Таким образом, наше уравнение приобретает вид:

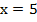
Выводы по уроку

Вывод: на данном уроке мы вспомнили основные определения касательно степени с натуральным показателем и ее основные свойства. Записали теоремы и решили примеры на их применение.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Школьный помощник (Источник).

2. Интернет-портал Math.sch1582.edusite.ru (Источник).