
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Рефлексия
КСП №59(1)
Инструкция: маршрутный лист может быть заполнен в электронном формате и отправлен на проверку учителю посредством системы «Кунделiк» или любого доступного мессенджера. При отсутствии такой возможности задания выполняются в тетради, фотографируются и отправляются учителю на проверку посредством доступного мессенджера.
| Предмет | Геометрия 10 |
| Ф.И.О. учителя | |
| Направление | ЕМН |
| Учебник | Смирнов В.А., Туяков Е.А., Геометрия 10 класс, ЕМН, Алматы: «Мектеп», 2019 |
| Урок № , тема урока | № 60(2). Уравнение прямой в пространстве |
| Цели обучения | 10.4.20 составлять каноническое уравнение прямой; 10.4.22 составлять уравнение прямой, проходящей через две заданные точки 10.4.21 - уметь переходить от канонического вида к параметрическому виду уравнения прямой |
| Ф.И. учащегося(заполняется учеником) |
| Порядок действий | Ресурсы (заполняется учителем) | Выполнение (заполняется учеником) |
| Изучи | 1)Составим уравнения прямой, проходящей через точку М0(x0,y0,z0) параллельно вектору 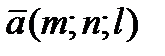 Определение 8.1. Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором.
Для любой точки М(x,y,z), лежащей на данной прямой, вектор
Определение 8.1. Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором.
Для любой точки М(x,y,z), лежащей на данной прямой, вектор  коллинеарен направляющему вектору а. Поэтому имеют место равенства: коллинеарен направляющему вектору а. Поэтому имеют место равенства:
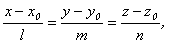 называемые каноническими уравнениями прямой в пространстве.
2)В частности, если требуется получить уравнения прямой, проходящей через две точки:
М1(х1, у1, z1) и M2(x2, y2, z2), направляющим вектором такой прямой можно считать вектор М1М2 ={x2 – x1, y2 - y1, z2 - z1}, и уравнения принимают вид: называемые каноническими уравнениями прямой в пространстве.
2)В частности, если требуется получить уравнения прямой, проходящей через две точки:
М1(х1, у1, z1) и M2(x2, y2, z2), направляющим вектором такой прямой можно считать вектор М1М2 ={x2 – x1, y2 - y1, z2 - z1}, и уравнения принимают вид:
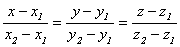 -
уравнения прямой, проходящей через две данные точки.
Посмотри видео, пройдя по ссылке:
Параметрические уравнения прямой в пространстве
Если известна точка -
уравнения прямой, проходящей через две данные точки.
Посмотри видео, пройдя по ссылке:
Параметрические уравнения прямой в пространстве
Если известна точка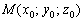 , принадлежащая прямой, и направляющий вектор , принадлежащая прямой, и направляющий вектор данной прямой, то параметрические уравнения этой прямой задаются системой: данной прямой, то параметрические уравнения этой прямой задаются системой:
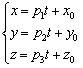 Пример
Составить параметрические уравнения следующих прямых:
Пример
Составить параметрические уравнения следующих прямых: 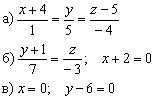 Решение: Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.
а) Из уравнений
Решение: Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.
а) Из уравнений  снимаем точку и направляющий вектор: снимаем точку и направляющий вектор: 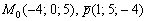 . Точку можно выбрать и другую (как это сделать – рассказано выше), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.
Составим параметрические уравнения данной прямой: . Точку можно выбрать и другую (как это сделать – рассказано выше), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.
Составим параметрические уравнения данной прямой: 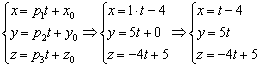 Удобство параметрических уравнений состоит в том, что с их помощью очень легко находить другие точки прямой. Например, найдём точку
Удобство параметрических уравнений состоит в том, что с их помощью очень легко находить другие точки прямой. Например, найдём точку 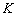 , координаты которой, скажем, соответствуют значению параметра , координаты которой, скажем, соответствуют значению параметра  : :  Таким образом:
Таким образом: 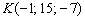 б) Рассмотрим канонические уравнения б) Рассмотрим канонические уравнения 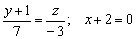 . Выбор точки здесь несложен, но коварен: . Выбор точки здесь несложен, но коварен: 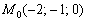 (будьте внимательны, не перепутайте координаты!!!). Как вытащить направляющий вектор? Можно порассуждать, чему параллельна данная прямая, а можно использовать простой формальный приём: в пропорции находятся «игрек» и «зет», поэтому запишем направляющий вектор (будьте внимательны, не перепутайте координаты!!!). Как вытащить направляющий вектор? Можно порассуждать, чему параллельна данная прямая, а можно использовать простой формальный приём: в пропорции находятся «игрек» и «зет», поэтому запишем направляющий вектор 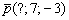 , а на оставшееся место поставим ноль: , а на оставшееся место поставим ноль: 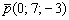 .
Составим параметрические уравнения прямой: .
Составим параметрические уравнения прямой: 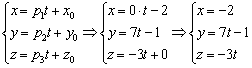 в) Перепишем уравнения
в) Перепишем уравнения 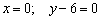 в виде в виде 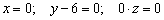 , то есть «зет» может быть любым. А если любым, то пусть, например, , то есть «зет» может быть любым. А если любым, то пусть, например, 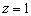 . Таким образом, точка . Таким образом, точка 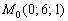 принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях 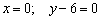 находятся «икс» и «игрек», и в направляющем векторе на данных местах записываем нули: находятся «икс» и «игрек», и в направляющем векторе на данных местах записываем нули: 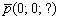 . На оставшееся место ставим единицу: . На оставшееся место ставим единицу: 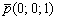 . Вместо единицы подойдёт любое число, кроме нуля.
Запишем параметрические уравнения прямой: . Вместо единицы подойдёт любое число, кроме нуля.
Запишем параметрические уравнения прямой: 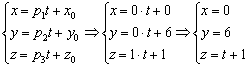
| Отметь знаком «+» материал, с которым ознакомился |
| Повтори: | 1.Повтори все действия с векторами в пространстве 2. Повтори уравнение сферы, уравнение плоскости | Устно |
| Выполни: | Решение задач.
Задача
Составить параметрические уравнения следующих прямых: 

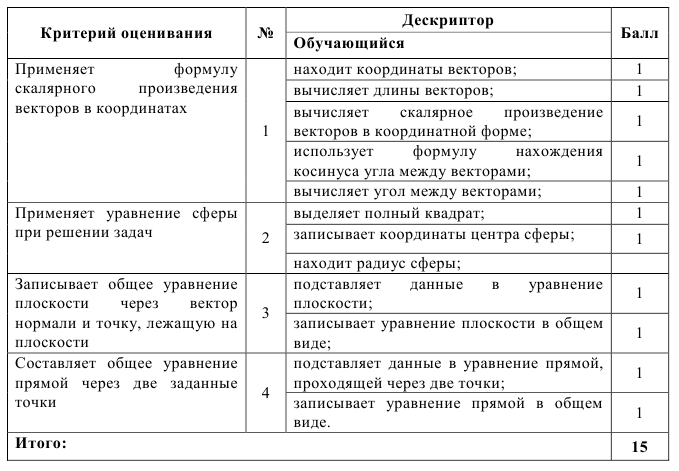
| Запиши решение в тетради и отошли учителю. |
Рефлексия