Хелпикс

Главная

Контакты

Случайная статья



Тест по теме: «Вписанная и описанная окружности» (8 класс)



Тест по теме: «Вписанная и описанная окружности» (8 класс)

1 вариант

  1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
  2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
  3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
  4. Около любого треугольника можно ___________________________.
  5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
  6. Центром вписанной в треугольник окружности является точка пересечения:

- Биссектрис треугольника

- Высот треугольника

- Медиан треугольника

- Серединных перпендикуляров к сторонам треугольника.

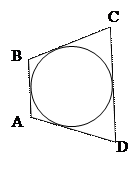  1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

- AB+BC=AD+CD;  - AB+CD=BC+AD;

- AB+AD=BC+CD;  - AD·BC=AB·CD.

  1. Описанная около треугольника

окружность изображена на рисунке:

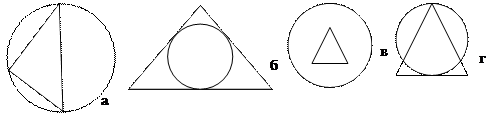
  1. Вписанная в четырехугольник окружность изображена на рисунке:

  1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

2 вариант

  1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
  2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
  3. В четырехугольник можно вписать окружность, если __________________________________________________________.
  4. В любой треугольник можно ___________________________.
  5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
  6. Центром описанного около окружности треугольника является точка пересечения:

- Высот треугольника

- Серединных перпендикуляров к сторонам треугольника

- Биссектрис треугольника

- Медиан треугольника.

  1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

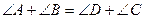- ;  - AB+CD=BC+AD;

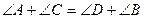- ;  - AD·BC=AB·CD.

  1. Вписанная в треугольник

окружность изображена на рисунке:

  1. Описанная около четырехугольника окружность изображена на рисунке:

  1. Около треугольника можно описать только ____________________.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.