Матричным способом.

РАЗДЕЛ VI

Теория графов

Графомназывается набор точек (эти точки называются вершинами), некоторые из которых объявляются смежными (или соседними). Считается, что смежные вершины соединены между собой ребрами (или дугами).

Обозначение:G=(S,U), где S- множество вершин графа, U- множество ребер.

Число вершин графа G=(S,U) называется егопорядком.

Граф называется ориентированным (или орграфом), если некоторые ребра имеют направление. Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Геометрически граф часто изображают точками плоскости, причем соседние вершины соединены дугами (для орграфа некоторые дуги имеют направление, что обычно отмечают стрелкой).

Мультиграфом называется граф без петель.

Простым графом называется мультиграф без кратных ребер.

Неориентированный граф называетсядвудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям (если его вершины можно правильно покрасить в два цвета).

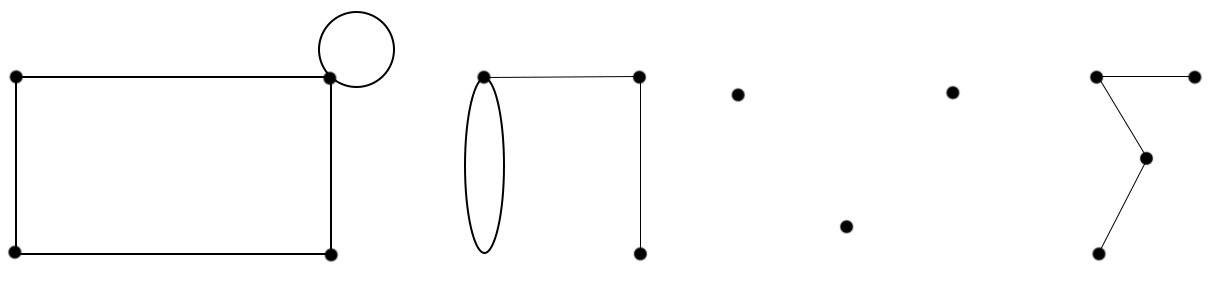
Пример 1:


Граф	Граф Мультиграф	Граф Мультиграф Простой граф	Граф Мультиграф Простой граф

1. Степени вершин графа

Число ребер графа G, инцидентных данной вершине 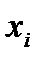называется степенью (валентностью) данной вершины и обозначается .

Вершина называется изолированной,если ее степень равна нулю.

Вершина называется висячей,если ее степень равна единице.

Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой.

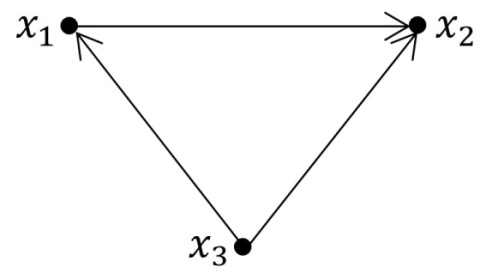
Полустепенью исхода (захода) вершины 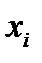оргафа называется число 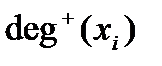( 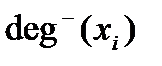) его дуг, исходящих из вершины 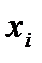(заходящих в вершину )

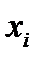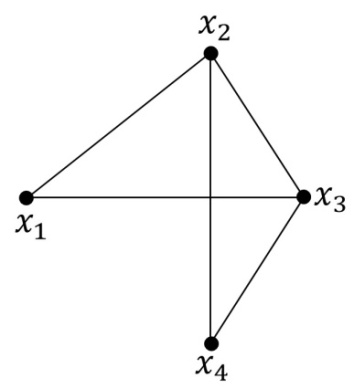
Пример 2:

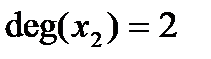
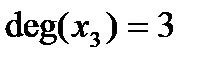
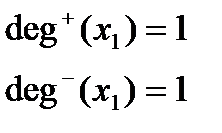
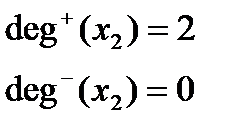
2. Способы задания графа

1. Перечислениемвершин и ребер.

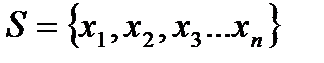
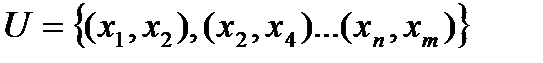
2. Графическим способомс помощью диаграммы.

3. Матричным способом.

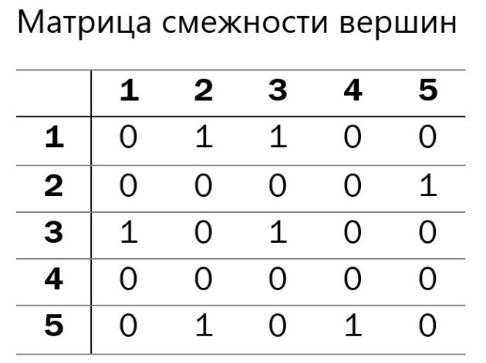
1) Матрицей смежности вершинграфа G=(S,U) порядка n называется квадратная матрица порядка n, строки и столбцы которой соответствуют вершинам графа, где элементы 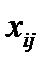равны числу дуг, идущих из i-ой вершины, в j-ую.

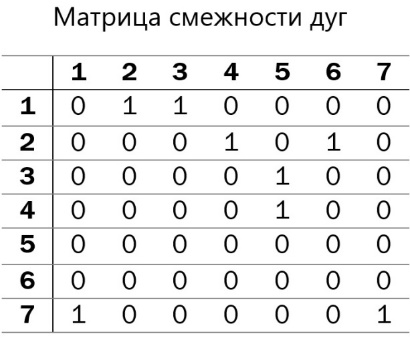
2) Матрицей смежности дугграфа G=(S,U),где 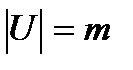, называется квадратная матрица, порядка m, элементы которой 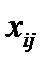равны единице, если дуга 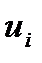непосредственно предшествует дуге 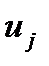, и равны нулю в остальных случаях.

3) Матрица инцидентности–одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам.

Пример 3:

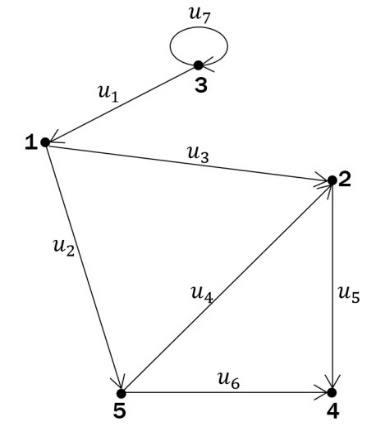
Для данного графа построить матрицы смежности вершин и дуг.

3. Маршруты, цепи и циклы

Маршрутв графе – это последовательность соседних (смежных) вершин. Ясно, что можно определить маршрут и как последовательность смежных ребер (в этом случае ребра приобретают направление). Заметим, что в маршруте могут повторяться вершины, но не ребра. Маршрут называется циклом, если в нем первая вершина совпадает с последней.

Путь (простая цепь)в графе (иногда говорят простой путь) – это маршрут без повторения вершин (а значит, и ребер).

Контур (простой цикл)– это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.

Пример 4:

Пример незамкнутого маршрута:

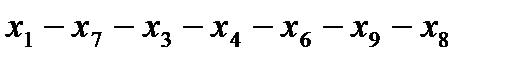
Пример замкнутого маршрута:

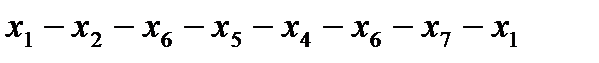
Пример цепи:

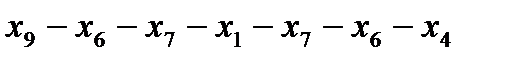
Пример пути (простой цепи):

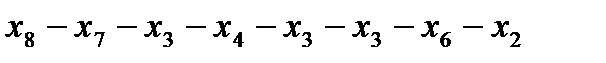
Пример цикла:

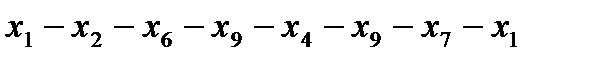
Пример контура (простого цикла):

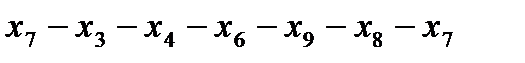
4. Метрические характеристики графа

Расстоянием между вершинам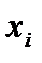и и 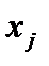называется длина кратчайшего маршрута соединяющего эти вершины и обозначается .

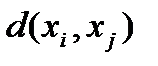Эксцентриситетом вершины 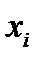называется величина, которая равна расстоянию от данной вершины до наиболее отдаленной от нее и обозначается .

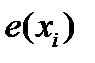Диаметром графаназывается максимальный из всех эксцентриситетов графа и обозначается .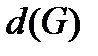

Вершина 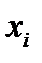называется периферийной, если .

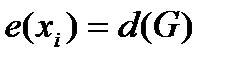Радиусом графаназывается минимальный из всех эксцентриситетов вершин и обозначается .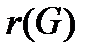

Вершина 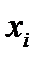называется центральной, если 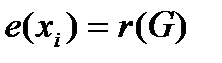. Множество всех центральных вершин называется центром графа.

5. Виды графов

Дерево – связный граф без циклов.

Связанный граф – если все его вершины связаны.

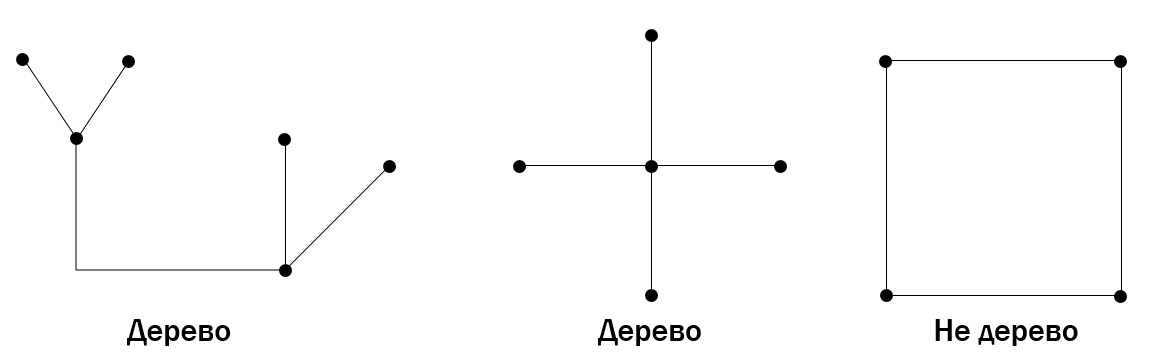
Лес (или ациклический граф) – неограф без циклов (может быть и несвязным).

Теорема. Для неографа G с n вершинами без петель следующие условия эквивалентны:

· G – дерево;

· G – связный граф, содержащий n-1 ребро;

· G – ациклический граф, содержащий n-1 ребро;

· Любые две несовпадающие вершины графа G соединяет единственная цепь.

· G – ациклический граф, такой, что если в него добавить одно ребро, то в нем появится ровно один цикл.

Остов (каркас) связного графа – дерево, содержащее все вершины графа. Определяется неоднозначно.

Редукция графа – остов с наибольшим числом ребер.

Корень дерева –вершина с нулевой степенью захода.

Узел ордерева – вершина, отличная от корня.

Листом ордереваназывается вершина 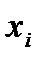, такая, что 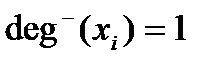и .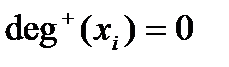

Ветвью ордерева называется путь из корня в лист.

Высотой дерева является длина его наибольшей ветви.

Эйлеровым циклом (путем) графа называется цикл (путь), содержащий все ребра графа ровно один раз. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.

Теорема:Граф G является эйлеровым тогда и только тогда, когда G – связный и все его вершины имеют четную степень.

Гамильтоновым циклом (путем) графа G называется цикл (путь), проходящий через каждую вершину G в точности по одному разу. Граф, обладающий гамильтоновым циклом, называется гамильтоновым.

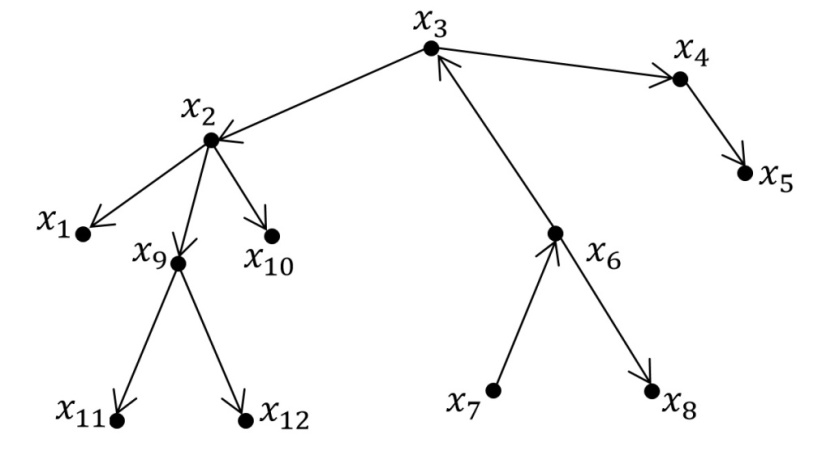Пример 1: Корень дерева- вершина 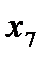. Все остальные вершины являются его узлами. Вершины 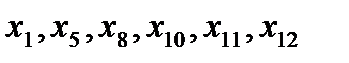- листы дерева. Путь .

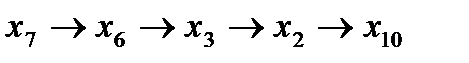Задачи

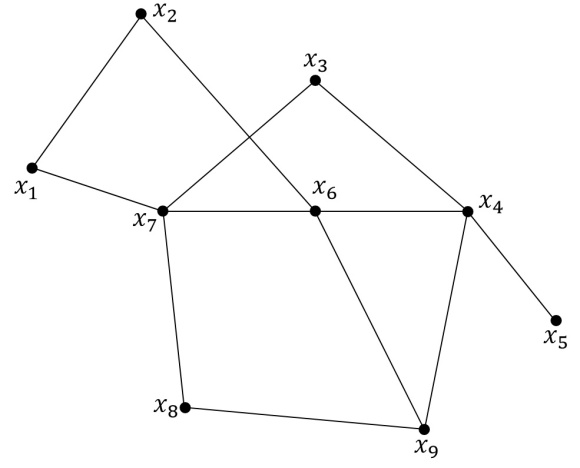
1. Перечислите мультиграфы, простые графы, двудольные и полные графы. Назовите порядок каждого графа.

2. Найдите степени вершин графов, изображенных на рисунке, полустепени исхода и захода.

3. Для графа, изображенного на рисунке построить матрицу смежности вершин, дуг и матрицу инцидентности.

4. Приведите примеры (незамкнутого) маршрута, замкнутого маршрута, цепи (не являющейся простой), простой цепи, цикла (не являющегося простым), простого цикла.

5. Найти эксцентриситеты вершин, радиусы и диаметры графа G, изображенного на рисунке и центральные вершины.

6. Для данного графа постройте матрицу смежности дуг, вершин, матрицу инцидентности. Найдите эксцентриситеты вершин, радиус графа, центр графа и его центральные вершины.

7. В шахматном турнире участвовали 4 человека. Каждый спортсмен сыграл со всеми другими участниками соревнований по одному разу. Сколько всего было сыграно партий?

8. На лесной опушке встретились заяц, белка, лиса, волк, медведь и куница. Каждый, здороваясь, пожал каждому лапу. Сколько всего лапкопожатий было сделано?

9. В первенстве класса по шашкам 5 участников: Аня, Боря, Влад, Гриша, Даша. Первенство проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему времени некоторые игры уже проведены: Аня сыграла с Борей, Владом и Дашей; Боря сыграл, как уже говорилось, с Аней и еще с Гришей; Влад – с Аней и Дашей, Гриша – с Борей, Даша – с Аней и Гришей. Сколько игр проведено к настоящему времени и сколько еще осталось?

10. В столовой на горячее можно заказать щуку, грибы и баранину, на гарнир – картофель и рис, а из напитков – чай и кофе. Сколько различных вариантов обедов можно составить из указанных блюд?

11. Из наборного полотна взяли 2 карточки с цифрой 1 и 3 карточки с цифрой 5. Сколько различных пятизначных чисел можно составить из этих карточек?

12. В одном классе учатся Иван, Петр и Сергей. Их фамилии Иванов, Петров и Сергеев. Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым