Рассмотрим свойства объёмов.

Название дисциплины: «Математика»
Номер группы: ТОР 19-1
Форма и дата занятия: Комбинированный урок 16.05.2020 г.
ФИО преподавателя: Раимгулова Зулейха Фазыловна raimgulova1961@mail.ru
Срок выполнения (сдачи) задания: 16.05.2020г.

Дата консультации: 16.05.2020

Задание:Изучить теоретический материал и выполнить практическую работу

Тема: 1. Практическая работа №67 «Тела и поверхности вращения».2. Объём и его измерение.

Презентация https://infourok.ru/metodicheskaya-razrabotka-uroka-po-teme-obem-i-ego-izmerenie-integralnaya-formula-obema-s-primeneniem-tehnologii-moderacii-3119680.html

Теоретический материал для самостоятельного изучения

https://resh.edu.ru/subject/lesson/4904/conspect/280335/

С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.

Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.

Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма(единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см³). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм³), кубический метр (1 м³) и тому подобное.

Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метров в бассейне и так далее.

Объём обозначается заглавной латинской буквой V.

Пример:

Объём книги400 кубических сантиметров запишут: V = 400см³.

Рассмотрим свойства объёмов.

Свойство № 1.Равные тела имеют равные объёмы.Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.

Свойство № 2.Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Задача. Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.

Решение:

Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора: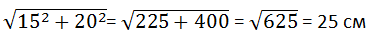

А теперь найдём объём параллелепипеда:

V = 15 ∙ 20 ∙ 25 = 7500 см³

Ответ: V = 7500 см³.

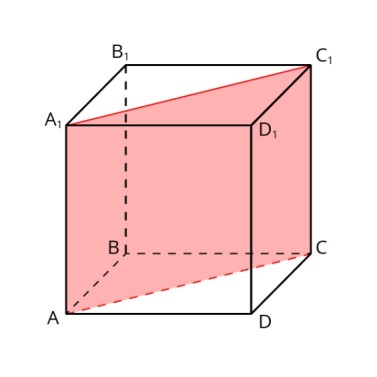
2. Найдите площадь закрашенной фигуры, если объём прямоугольного параллелепипеда равен 960 см³, AB = 8 см, АА₁ ₌20 см.

12 Следующая ⇒