Вывод формулы для вычисления расстояния между двумя точками на плоскости

⇐ ПредыдущаяСтр 2 из 2

Вопрос 8

Даны точки А(–6; 0; 1), В(–7; 1; 1), С(0; 6; 0), Д(3; –2; 0). Какие из этих точек лежат на оси Ох?

Варианты ответов

· точка Д

· точка А

· нет точек, лежащих на оси Ох

Вопрос 9

Дана точка М(–6; 4; –1). Тогда координаты основания перпендикуляра, опущенного из точки М на ось Оz равны...

Варианты ответов

· М(0; 0; 0)

· М(0; 0; - 1)

· М(- 6; 4; 0)

Вопрос 10

Дана точка М(–6; 4; –1). Тогда координаты основания перпендикуляра, опущенного из точки М на плоскость xOz равны.

Варианты ответов

· N( 0; 4; 0)

· N( 0; 0; - 1)

· N(- 6; 0; - 1)

Определение. Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.

Формула вычисления расстояния между двумя точками A(x_a, y_a) и B(x_b, y_b) на плоскости:

AB = √(x_b - x_a)² + (y_b - y_a)²

Формула вычисления расстояния между двумя точкамиA(x_a, y_a, z_a) и B(x_b, y_b, z_b) в пространстве:

AB = √(x_b - x_a)² + (y_b - y_a)² + (z_b - z_a)²

Вывод формулы для вычисления расстояния между двумя точками на плоскости

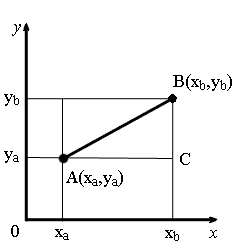
Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x_b - x_a;
BC = y_b - y_a.

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

AB = √AC² + BC².

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.

Примеры вычисления расстояния между двумя точками на плоскости

Пример 1.

Найти расстояние между точками A(-1, 3) и B(6,2).

Решение.

AB = √(x_b - x_a)² + (y_b - y_a)² = √(6 - (-1))² + (2 - 3)² = √7² + 1² = √50 = 5√2

Ответ: AB = 5√2.

Пример 2.

Найти расстояние между точками A(0, 1) и B(2,-2).

Ссылка на сообщество МАТЕМАТИКА в контакте https://vk.com/club194177059

⇐ Предыдущая 12