
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Скалярное произведение векторов.
Скалярное произведение векторов.
План
1. Скалярное произведение векторов.
2. Угол между векторами
3. Примеры
Вопрос 1. Скалярное произведение векторов.
Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними:
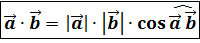 .
.
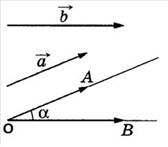
Два вектора 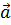 и
и 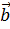 называются перпендикулярными, если угол между ними равен 90°. В этом случае косинус равен нулю, и соответственно
называются перпендикулярными, если угол между ними равен 90°. В этом случае косинус равен нулю, и соответственно 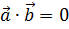 . Таким образом скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
. Таким образом скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Скалярное произведение 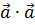 называется скалярным квадратом вектора
называется скалярным квадратом вектора 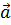 и обозначается
и обозначается 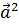 . Таким образом скалярный квадрат вектора равен квадрату его длины.
. Таким образом скалярный квадрат вектора равен квадрату его длины.
Скалярное произведение двух векторов 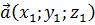 и
и 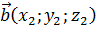 выражается формулой:
выражается формулой:
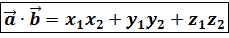 .
.
Основные свойства скалярного произведения векторов:
1. 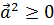
2. 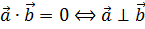
3. Переместительный закон 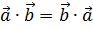
4. Сочетательный закон 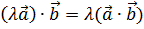
5. Распределительный закон 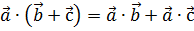
Вопрос 2. Угол между векторами
Из определений скалярного произведения векторов легко вывести формулу для косинуса угла между двумя векторами:
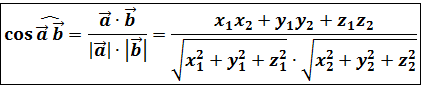
Если необходимо найти угол между двумя прямыми, а не векторами, то следует действовать следующим образом.
Пусть даны две прямые a и b, и их направляющие вектора 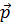 и
и 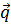 , заданные координатами. Найдем угол β между прямыми.
, заданные координатами. Найдем угол β между прямыми.
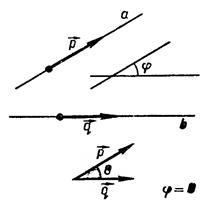
Возможны два случая:
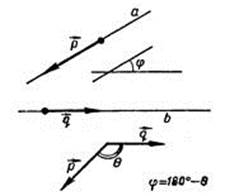
| 1) Если угол φ между векторами острый, то угол φ равен углу β между прямыми. | 2) Если угол φ между векторами тупой, то угол между прямыми равен – (180-φ). |
| 
|
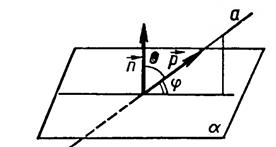 Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.
Если нам известен направляющий вектор 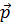 прямой a и вектор
прямой a и вектор  , перпендикулярный плоскости α (вектор
, перпендикулярный плоскости α (вектор  - это вектор нормали), то мы можем выразить угол между прямой и плоскостью через угол между данной прямой и прямой, перпендикулярной плоскости α:
- это вектор нормали), то мы можем выразить угол между прямой и плоскостью через угол между данной прямой и прямой, перпендикулярной плоскости α:
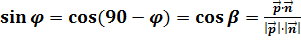
Вопрос 3. Примеры
Рассмотрим задачу на нахождение скалярного произведения векторов.
Задача 1. Дано: ABCDA1B1C1D1 – куб, O1 – центр A1B1C1D1 , AB=a.
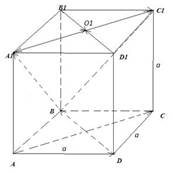 Найти скалярные произведения векторов:
Найти скалярные произведения векторов:
а) 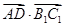 . Находим эти вектора на рисунке, они сонаправлены, значит угол между ними 0°, а эти вектора равны a. Получаем:
. Находим эти вектора на рисунке, они сонаправлены, значит угол между ними 0°, а эти вектора равны a. Получаем: 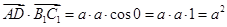
б) 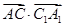 . Эти вектора параллельны и противоположно направлены, значит, угол между ними 180°. Модуль вектора
. Эти вектора параллельны и противоположно направлены, значит, угол между ними 180°. Модуль вектора 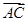 - это диагональ квадрата,
- это диагональ квадрата,  ,
, 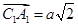 . Получаем:
. Получаем: 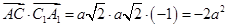 .
.
в) 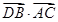 . Так как эти вектора перпендикулярны (по рисунку), то косинус угла между ними равен 0. Значит,
. Так как эти вектора перпендикулярны (по рисунку), то косинус угла между ними равен 0. Значит, 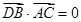 .
.
г) 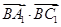 . Модули этих векторов равны
. Модули этих векторов равны 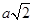 - это диагонали квадратов. Чтобы найти угол между нужными векторами, рассмотрим треугольник A1C1B. Этот треугольник равносторонний, значит, угол равен 60°.
- это диагонали квадратов. Чтобы найти угол между нужными векторами, рассмотрим треугольник A1C1B. Этот треугольник равносторонний, значит, угол равен 60°.
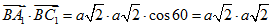 ·
· 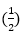 = - 2a2
= - 2a2
д) 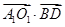 . Эти вектора перпендикулярны, значит,
. Эти вектора перпендикулярны, значит, 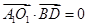 .
.
е) 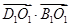 . Длины этих векторов равны
. Длины этих векторов равны 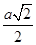 , так как они являются половинами диагоналей. Эти векторы противоположно направлены, угол между ними 180°.
, так как они являются половинами диагоналей. Эти векторы противоположно направлены, угол между ними 180°.
Получаем: 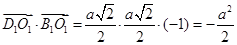 .
.
Рассмотрим задачу на нахождение угла между прямыми и угла между прямой и плоскостью.
Задача 2. Дано: правильная треугольная призма ABCA1B1C1, 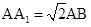 .
.
Найдите:
а) угол между прямыми АС1 и A1B;
б) угол между прямой АС1 и плоскостью АВС.
Решение: Пусть AB=a, тогда AA1=a√2. Введем прямоугольную систему координат с центром в точке С, и определим координаты точек A, B, C1 и A1: 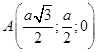 ,
, 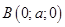 ,
,  ,
, 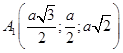 .
.
Зная координаты конца и начала векторов, находим координаты векторов: 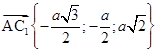 ,
, 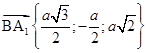 .
.
б) Так как призма правильная, следовательно 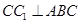 . Чтобы найти угол между плоскостью и прямой необходимо знать вектор
. Чтобы найти угол между плоскостью и прямой необходимо знать вектор 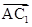 и вектор, перпендикулярный плоскости ABC – вектор нормали
и вектор, перпендикулярный плоскости ABC – вектор нормали 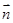 ,
, 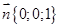 . Находим угол между прямой и плоскостью:
. Находим угол между прямой и плоскостью:
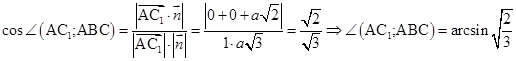
С помощью скалярного произведения можно также найти угол между двумя плоскостями. Рассмотрим две плоскости α и β с нормальными векторами 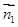 и
и 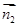 . Угол φ между плоскостями α и β можно выразить через угол
. Угол φ между плоскостями α и β можно выразить через угол 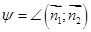 .
.
Возможны два случая:
1) Если ψ ≤ 90°, то φ = ψ;
2) Если ψ > 90°, то φ = 180°-ψ .
Значит, угол φ можно найти по формуле: 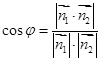 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|