Пример решения задачи на нахождение емкости системы проводников.

Лекция 4.

ЭЛЕКТРОСТАТИКА ПРОВОДНИКОВ

Проводником называют тело, в котором электрические заряды могут свободно перемещаться. Хорошими проводниками являются металлы. Любое, даже малое внешнее электрическое поле вызывает в них движение электронов против поля. Если, однако, тело изолировано, такое движение не может продолжаться долго, так как приводит к накоплению избыточного количества электронов с одной стороны проводника, куда входят линии поля. В этом месте образуется отрицательный заряд. С противоположной стороны проводника, где образуется недостаток электронов, возникает положительный заряд. Эти две разноименно заряженные области проводника создают собственное внутреннее электрическое поле, которое суммируется с внешним электрическим полем. Как видно из рис.4.1 внутри тела напряженности внешнего и внутреннего полей противоположны друг другу, то есть внутри проводника они вычитаются.

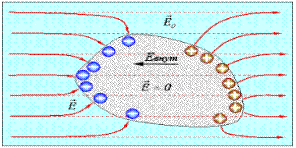Рис. 4.1

Перемещение электронов происходит до тех пор, пока напряженности этих двух полей не уравняются. В состоянии равновесия суммарная напряженность внутри проводника равна нулю и разделенные заряды остаются неподвижными. Такое равновесие полей (и зарядов) устанавливается автоматически и является устойчивым. В состоянии равновесия напряженность поля всюду внутри проводника равна нулю.

Е_внутр = 0 (4.1)

Если учесть установленную ранее связь напряженности поля и его потенциала

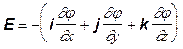то из условия (4.1) можно заключить, что потенциал внутри проводника постоянен (j = const).

Однако одного условия (4.1) недостаточно, чтобы обеспечить неподвижность зарядов внутри проводника. Линии электрического поля должны подходить к поверхности проводника по нормали к ней. В противном случае была бы отлична от нуля тангенциальная составляющая поля Е_t, которая вызывала бы движение электронов вдоль поверхности. Таким образом, вторым необходимым условием равновесия зарядов в проводнике является

Е_t = 0, то есть Е = Е_n (4.2)

Из условия (4.2) вытекает, что работа по перемещению любого заряда по поверхности проводника равна нулю, так как это перемещение будет происходить перпендикулярно линиям электрического поля (cosα = 0). Отсюда следует, что поверхность проводника является эквипотенциальной поверхностью.

Рассмотрим теперь проводник, которому сообщили некоторый внешний заряд q. Он быстро перераспределится внутри проводника так, чтобы соблюдались условия равновесия (4.1), (4.2). При этом избыточные заряды окажутся распределенными по поверхности проводника. Чтобы показать это, мысленно выделим внутри проводника произвольную замкнутую поверхность. Поскольку Е_внутр = 0, поток вектора напряженности электрического поля через нашу поверхность также будет равен нулю. На основании теоремы Гаусса можно утверждать, что избыточные заряды внутри поверхности отсутствуют. Это утверждение сохраняет силу для любой замкнутой поверхности внутри проводника, следовательно, избыточный заряд q, сообщенный проводнику, может распределиться только по его наружной поверхности. К такому же выводу можно прийти, если учитывать, что одноименные заряды отталкиваются и стремятся расположиться на максимальном расстоянии друг от друга.

Заряженная поверхность проводника создает вне его электрическое поле. В непосредственной близости от поверхности можно пренебречь ее кривизной и считать, что поле в прилегающих точках создается участком заряженной плоской поверхности. Исходя из этого, напряженность поля вблизи поверхности заряженного проводника можно приближенно вычислять по аналогии с полем заряженной плоскости по формуле

Е » s/e₀, (4.3)

где s - поверхностная плотность избыточных зарядов в проводнике. Напряженность этого поля вдвое больше, чем у поля равномерно заряженной плоскости (формула (2.6)). Это различие обусловлено тем, что бесконечная заряженная плоскость создает поток вектора напряженности по обе стороны от плоскости, а в случае конечного проводника этот поток концентрируется только в одну наружную сторону от его поверхности (внутри проводника поле равно нулю).

Возьмем заряженный проводник, поверхность которого имеет острые концы (рис.4.2). На большом расстоянии от него, намного превышающем его размеры, поле проводника практически будет совпадать с полем точечного заряда, поэтому эквипотенцтальные поверхности будут иметь форму сферы (см. рис.4.2). Но по мере приближения к проводнику, эквипотенциальные поверхности по своей форме будут все более подобны форме самого проводника, и это вполне понятно, ведь поверхность проводника, как мы обсудили выше, сама является эквипотенциальной поверхностью.

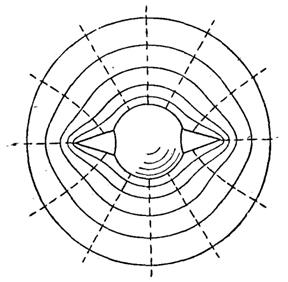Рис.4.2

Из рисунка видно, что эквипотенциальные поверхности вблизи выступов располагаются гуще, следовательно напряженность электрического поля там выше, а это согласно (4.3) означает, что и поверхностная плотность зарядов на острых концах также выше, чем на ровной поверхности. Ниже будет показано, что поверхностная плотность зарядов на поверхности проводника обратно пропорциональна радиусу кривизны поверхности. На остриях, где радиус кривизны очень мал, плотность зарядов и напряженность поля может достигать таких величин, что начнут ионизироваться молекулы воздуха, и ионы иного знака будут притягиваться к острию, уменьшая заряд проводника. Заряд будет как бы стекать с острия. Такое явление ограничивает возможности накопления слишком больших зарядов в одиночных проводниках.

Введем важную характеристику, отображающую способность различных проводников накапливать заряды. Рассмотрим для примера проводящую сферу радиуса R, удаленную от других тел. Ее поле имеет такой же вид, как поле точечного заряда. Если сообщить сфере заряд q, то согласно формуле (2.18) потенциал на ее поверхности будет равен

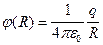(4.4)

Мы видим, что потенциал j заряженной сферы прямо пропорционален величине ее заряда q. Опыт показывает, что пропорциональность заряда и потенциала соблюдается и для проводников любой формы. Исходя из этого, можно написать

q = Cj (4.5)

где С - коэффициент пропорциональности, называемый электроемкостью или просто емкостью уединенного проводника.

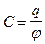(4.6)

Емкость проводника зависит от его размеров и формы, но не зависит от свойств материала проводника. Емкость шара радиуса R можно найти, подставив (4.4.) в (4.6). В результате получим

C = 4pe₀R. (4.7)

Единица электроемкости - фарад (Ф). Фарад - это емкость проводника, потенциал которого повышается на 1В при сообщении ему заряда в 1Кл. Пользуясь формулой (4.7), можно подсчитать, что емкостью в 1Ф обладает шар, радиусом в 9 млн. км, то есть фарад – это очень крупная единица емкости. На практике используют дольные единицы емкости - микрофарад (10^-6Ф) и пикофарад (10^-12Ф). Из формулы (4.7) непосредственно следует, что ε₀= С/4πR, то есть электрическая постоянная должна измеряться в фарадах на метр.

Что происходит с емкостью проводников при их соединении? Рассмотрим две проводящие сферы с радиусами R₁ и R₂, содержащие заряды, и соединим их между собой тонким проводником (рис.4.3). По этому проводнику заряды начнут перетекать до тех пор, пока потенциалы φ₁ и φ₂ обеих сфер не сравняются, ведь поверхность любого проводника, как мы установили выше, является эквипотенциальной поверхностью (здесь можно провести аналогию с сообщающимися сосудами). Общий потенциал φ соединенных сфер будет равен

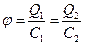(4.8)

где Q₁, Q₂ – заряды сфер, а С₁ , С₂их емкости.

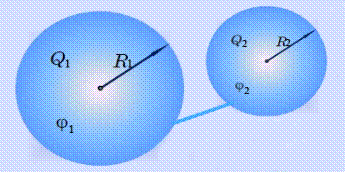
Рис.4.3

По определению емкости, у такого составного проводника емкость будет равна отношению суммарного заряда сфер Q_сум к их общему потенциалу φ

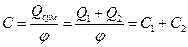(4.10)

Итак, из формулы (4.10) следует, что при соединении одиночных проводников их емкости складываются.

Выразим заряды Q₁ и Q₂ через поверхностные плотности зарядов σ₁ и σ₂

Q₁ = 4πR₁²σ₁, Q₂ = 4πR₂²σ₂, (4.11)

а емкости С₁ и С₂ – через радиусы сфер (формула (4.7)). Подставив эти выражения в (4.8) получим

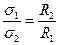(4.12)

Мы получили, что при соединении заряженных тел поверхностная плотность заряда будет обратно пропорциональна радиусу кривизны поверхности. Эта зависимость справедлива и для любого тела с переменной кривизной поверхности: там, где радиус кривизны меньше, плотность заряда оказывается выше. Этим объясняется упомянутая выше концентрация зарядов вблизи острия.

КОНДЕНСАТОРЫ

Уединенные проводники обладают малой емкостью. Например, емкость земного шара составляет всего 700 микрофарад. В технике часто возникает потребность в накоплении сравнительно больших зарядов при невысоком потенциале и малых размерах накопителя. Такую задачу невозможно решить с помощью одиночных проводников. Для ее решения созданы специальные устройства - конденсаторы. Принцип действия конденсаторов основан на том, что два близко расположенных противоположно заряженных проводника взаимно влияют на электрические поля друг друга, ослабляя их. Это приводит к снижению потенциала каждого из проводников, по сравнению со случаем, когда они удалены друг от друга. Снижение потенциала при неизменной величине заряда означает, согласно формуле (4.6), увеличение емкости. Под емкостью конденсатора понимают отношение заряда проводников к разности их потенциалов:

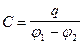(4.13)

Величина емкости конденсатора определяется геометрией и взаимным расположением проводников, а также, диэлектрической проницаемостью среды, в которой они находятся.

Рассмотрим два вида конденсаторов.

1. Плоский конденсатор состоит из двух параллельных пластин площадью S, называемых обкладками, расположенных на небольшом расстоянии d друг от друга (рис.4.4).

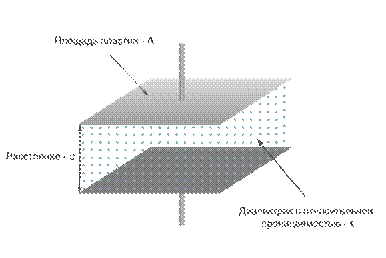
Рис.4.4

Промежуток между обкладками заполнен диэлектрической средой c диэлектрической проницаемостью e. Напряженность поля Е между пластинами согласно формуле (2.7) постоянна и равна σ/ε₀e. Тогда разность потенциалов между пластинами можно найти по формуле (2.28)

φ₁ – φ₂ = Еd = σd/ε₀ε (4.14)

Поверхностная плотность заряда σ выражается через величину заряда q на обкладках

σ = q/S. (4.15)

Тогда

(4.16)

Теперь, подставив (4.16) в формулу (4.13) находим емкость плоского конденсатора

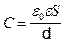(4.17)

Из этой формулы следует, что емкость плоского конденсатора тем больше, чем больше площадь обкладок и диэлектрическая проницаемость среды, разделяющей их, и чем меньше расстояние между обкладками.

Практически плоский конденсатор обычно изготовляют из двух тонких, узких и длинных лент металлической фольги 1, проложенных очень тонкой лентой диэлектрика 2 (рис.4.5).

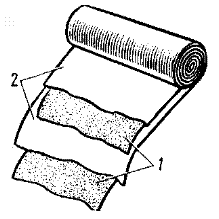Рис.4.5

Получающаяся трехслойная полоса свертывается плотным рулоном. Такой конденсатор, имея размеры спичечного коробка, может обладать емкостью больше земного шара. Еще большей емкостью при тех же размерах обладают электролитические конденсаторы, в которых роль диэлектрика выполняет тонкая пленка оксида алюминия (Al₂O₃) на поверхности полосы из алюминиевой фольги. Эта полоска фольги играет роль одной из обкладок (рис 4.6). В качестве другой обкладки выступает бумага, пропитанная электролитом (проводящим раствором). Фольга с бумагой также свернуты в рулон.

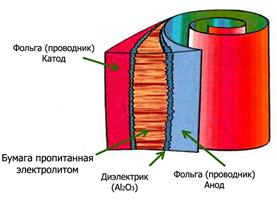
Рис.4.6

2.Сферический конденсатор. Он состоит из двух концентрических разноименно заряженных сфер с радиусами R₁и R₂, пространство между которыми заполнено диэлектриком Рис.4.7.

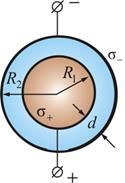
Рис. 4.7

Разность потенциалов между сферическими обкладкам можно найти, используя формулу (2.18) для потенциала поля точечного заряда. Эта формула применима и для описания потенциала заряженной сферы, поскольку мы уже убеждались (лекция 1) в том, что поле заряженной сферы вне ее ничем не отличается от поля точечного заряда. Поэтому потенциал φ₁ внутренней сферы будет равен

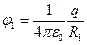. (4.18)

При этом мы учитываем, что в пространстве между сферами поле внешней сферы равно нулю. Потенциал внешней сферы φ₂ равен

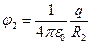(4.19)

В результате получим

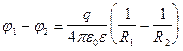(4.20)

Подставив (4.20) в (4.13) получим, что емкость сферического конденсатора равна

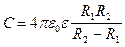(4.21)

Несколько конденсаторов можно объединить в батарею. Определим емкость конденсаторной батареи при параллельном и последовательном соединениях конденсаторов (рис.4.8).

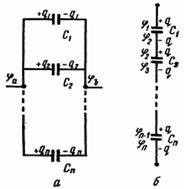
Рис. 4.8

У всех параллельно соединенных конденсаторов разность потенциалов на обкладках одинакова и равна φ_а – φ_b , так как обкладки соединены проводником (рис. 4.8 а). Сумма одноименных зарядов на обкладках q₁ + q₂ + q₃ + ... + q_n = q. Емкость С такой батареи равна

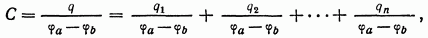
Поэтому

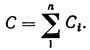(4.22)

где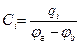

У последовательно соединенных конденсаторов (рис.4.8 б) заряды всех обкладок одинаковы по величине и равны q, а разность потенциалов

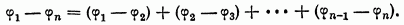
Емкость такой батареи

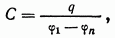(4.23)

Найдем от обеих частей уравнения (4.23) обратные величины:

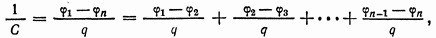
Слагаемые в правой части этого уравнения представляют собой величины, обратные емкостям С_i отдельных конденсаторов. Поэтому

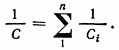(4.24)

Небезынтересно отметить, что орган для накапливания электрической энергии, имеющийся у некоторых рыб (электрический скат, электрический угорь и др.), представляет собой батарею конденсаторов значительной емкости, находящуюся под довольно высоким напряжением и развивающую при разряде большую мощность (у электрического угря напряжение достигает 1000 В, а разрядная мощность 1кВт. Эта батарея состоит из тонких чередующихся слоев проводящей (нервной) и непроводящей (соединительной) ткани. Напряжение генерируется специальными клетками – электроцитами за счет перекачки ионов калия и натрия через клеточную мембрану с помощью специальных насосов.

С помощью плоского конденсатора американский физик Милликен в 1909 г. впервые осуществил экспериментальное определение величины заряда электрона е. Идея опыта Милликена состояла в следующем.

Между горизонтально расположенными пластинами плоского конденсатора приложена разность потенциалов φ₁ – φ₂, измеряемая вольтметром V (рис.4.9).

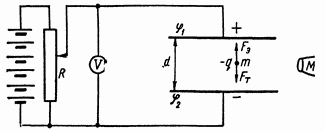
Рис.4.9

Расстояние между пластинами – d, нижняя пластина заряжена отрицательно. В пространство между пластинами вбрызгиваются посредством пульверизатора мельчайшие капельки жидкого масла, а воздух в этом пространстве ионизируется ультрафиолетовыми лучами. Образующиеся ионы могут присоединяться («прилипать») к масляным капелькам. В результате многие из капелек оказываются электрически заряженными.

На отрицательно заряженные капельки действуют две силы: направленная вниз сила тяжести

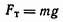(4.25)

и направленная вверх сила Кулона

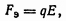(4.26)

где m - масса капельки, q -ее заряд, E напряженность электрического поля, g – ускорение силы тяжести. Наблюдая за одной из таких капелек с помощью микроскопа М и изменяя посредством потенциометра R разность потенциалов, можно подобрать такое значение φ₁ – φ₂, при котором капелька неподвижно повиснет в воздухе. Это означает, что по величине

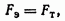
откуда

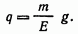(4.27)

Так как очень мелкие капельки практически шарообразны, то массу наблюдаемой капельки можно определить из очевидного соотношения

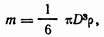(4.28)

где D - диаметр капельки, измеряемый с помощью микроскопа, ρ плотность масла. Подставив в формулу (4.27) выражение массы (4.28) и выражение для напряженности E = (φ₁ – φ₂)/d, получим соотношение

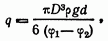(4.29)

позволяющее рассчитывать величину заряда q

На основе многочисленных измерений Милликен установил, что заряд q оказывается всегда или равным, или кратным некоторому элементарному заряду e т. е. заряду электрона.

Современные измерения заряда электрона усовершенствованным методом Милликена и другими методами показали, что

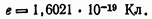
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Рис.4.10

Любое заряженное тело обладает энергией, потому что для сообщения заряда этому телу необходимо совершить определенную работу по переносу заряда. Вычислим, например, работу по зарядке конденсатора, то есть работу, которую необходимо совершить для сообщения одной из его обкладок заряда +q, а другой -q. Такую зарядку можно выполнить следующим образом. Будем переносить малые порции заряда dq с одной пластины на другую. При переносе первой порции заряда работа не совершается, так как электрическое поле в конденсаторе еще отсутствует. Однако оно появляется после перенесения этой порции, и перенос последующих порций требует совершения все большей работы, как так разность потенциалов j₁ - j₂между пластинами с накоплением заряда возрастает. Работа dA переноса очередной порции равна

dA = dq(j₁ - j₂) (4.30)

Эта работа идет на приращение dW энергии конденсатора. Выразив (j₁ - j₂) через заряд и емкость в соответствии с (4.13), получим

dW = dA = dq(q/C) (4.31)

Для нахождения полной энергии W конденсатора с зарядом q₀ и разностью потенциалов между обкладками j₁ - j₂= U, проинтегрируем (4.31) по dq.

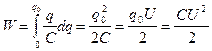(4.32)

Итак, энергия заряженного конденсатора

W = CU²/2 (4.33)

Разность потенциалов U между обкладками называют напряжением. Энергию конденсатора можно связать не только с напряжением, но и с напряженностью электрического поля между обкладками. Рассмотрим случай плоского конденсатора. Если подставить в формулу (4.33) значения С из (4.17), то получим

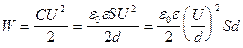(4.34)

Входящее в формулу (4.34) отношение U/d равно напряженности поля Е между обкладками. Произведение Sd представляет собой объем V, заключенный между обкладками, то есть объем, занимаемый электрическим полем. Таким образом,

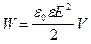(4.35)

Энергия заряженного конденсатора пропорциональна квадрату напряженности электрического поля между его обкладками.

Где сосредоточена энергия заряженного конденсатора, на его обкладках в виде зарядов или в электрическом поле, заключенном между ними (рис.4.11)?

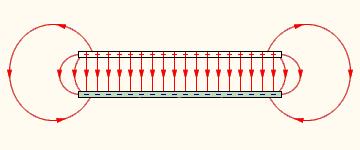
Рис.4.11

Опыты, с которыми мы познакомимся позднее, показывают, что переменные электрические поля, которые могут существовать независимо от зарядов, обладают энергией и способны переносить ее. Например, жизнь на Земле существует благодаря энергии электромагнитных волн, излучаемых Солнцем. Так что мы имеем полные основания полагать, что электрическое поле между обкладками конденсатора и является аккумулятором его энергии. Поскольку поле в плоском конденсаторе однородно, эта энергия равномерно распределена по всему объему V, заключенному между обкладками. Нетрудно подсчитать энергию поля w, заключенную в каждой единице объема.

w=W/V. (4.36)

Эту величину называют плотностью энергии поля. На основании (4.35) плотность энергии поля в конденсаторе равна

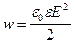(4.37)

Формула (1.61) сохраняет силу и для случая неоднородного электрического поля.

Пример решения задачи на нахождение емкости системы проводников.

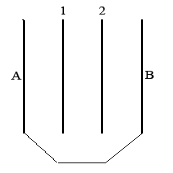Четыре одинаковые металлические пластины расположены на одинаковом расстоянии h друг от друга. Наружные пластины соединены проводником Рис.4.12. Площадь каждой пластины S. Найти емкость системы между точками 1 и 2.

Рис.4.12

12 Следующая ⇒