Критерии оценки выполнения работы

Критерии оценки выполнения работы

Менее 10 баллов – оценка «неудовлетворительно»

11-14 баллов – оценка «удовлетворительно»

15-19 баллов – оценка «хорошо»

20–23 балла – оценка «отлично»

Задание ___Экзаменационные задания – практические, выполняются письменно, ответы записываются в бланк ответов

(ознакомительный вариант)

№ п/п

Количество баллов

Задание

Бланк для ответов

Ответ на задание

Замена ошибочных ответов

Обязательная часть

1 балл

Найдите область определения функции

1 балл

Упростите

1 балл

Вычислите

1 балл

Найдите значение выражения 5^log₅⁹²

1 балл

Найдите корень уравнения

1 балл

Найдите значение выражения х²-2ху+у(2х-5), при х=5, у = -1,95

1 балл

Вычислите

1 балл

Найдите промежутки убывания функции

1 балл

Решите уравнение

1 балл

На каком из рисунков изображены графики нечетной функции?

1 балл

Определите, какие из перечисленных точек принадлежат графику функции у (х ) = 5х - 1. А (1; 0); В (0; –1); С (2; 2); Д (3; 5).

1 балл

Найдите производную функции f(x) = 5x² +155

1 балл

Сколько двузначных чисел можно составить из чисел 1,2,3,4,5

1 балл

Решите уравнение:

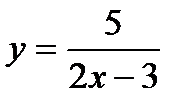
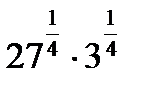
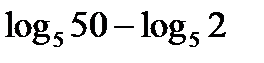
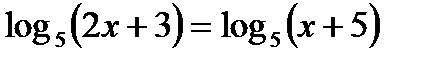
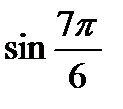
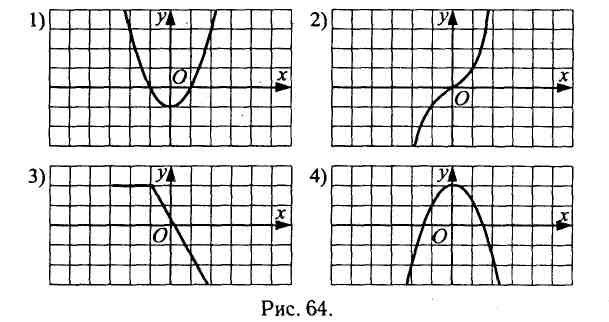
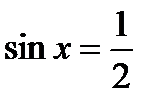
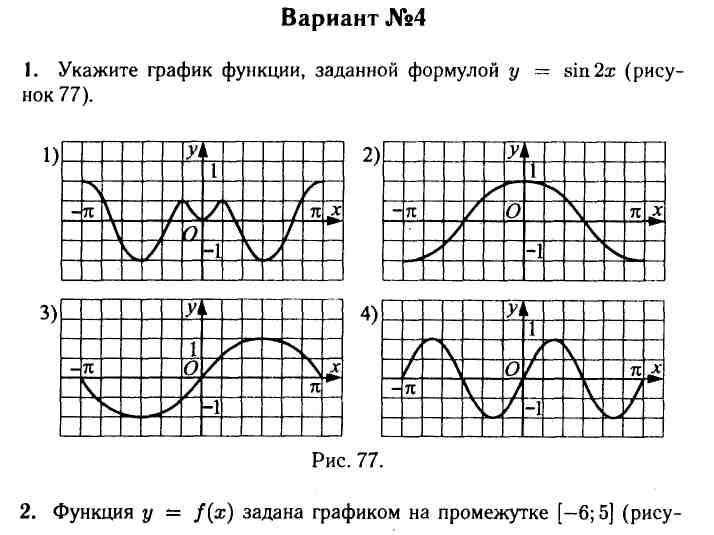
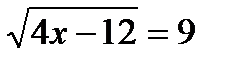
Дополнительная часть

3 балл

Найдите площадь боковой поверхности пирамиды, в основании которой лежит квадрат со стороной 8 см и апофемой равной 9 см

Решение полное с чертежом

2 балл

Постройте сечение, проходящее через три заданные точки:

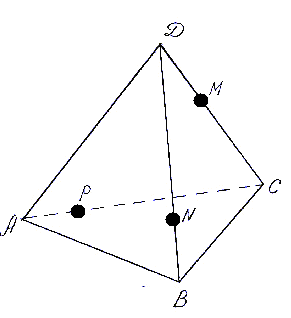
Чертеж на бланке

3 балл

Решите уравнение log²₃x – 5log₃x + 6 = 0

Решение полное

3 балл

Вычислите площадь фигуры, ограниченной линиями у = х²; у = 0; х = 3

Решение полное с чертежом