Хелпикс

Главная

Контакты

Случайная статья



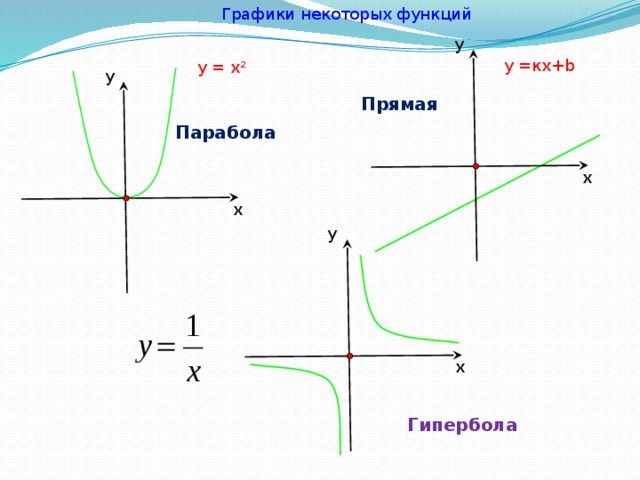
График функции. Построение графиков функции



График функции. Построение графиков функции

Линейная функция – функция вида y=ax+b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b:

 

Если a>0, прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y.

Если a<0, прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y.

Если a=0, функция принимает вид y=b.

 

Графиком функции y=ax2+bx+c является парабола.

 

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a,b,c:

  1. Коэффициент a указывает на то, куда направлены ветки параболы.
  • Если a>0 , ветки параболы направлены вверх.
  • Если a<0 , ветки параболы направлены вниз.
  1. Коэффициент c указывает, в какой точке парабола пересекает ось y.
  2. Коэффициент b помогает найти вxв – координату вершины параболы.

вxв=−b/2a

  1. Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
  • Если D>0 – две точки пересечения.
  • Если D=0 – одна точка пересечения.
  • Если D<0 – нет точек пересечения.

Графиком функции y=k/x является гипербола.

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

Если коэффициент k>0, то ветви гиперолы проходят через I и III четверти.Если k  <  0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y.

 

Задания

1.Построить график функции у= 2х+5, у= х2-3х+4, у= 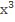+2

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.