
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Геометрия.9-а класс.20.05.2020. 9-б класс. 21.05.2020.
Тема урока: Повторение. Четырёхугольники
Мы продолжаем тренироваться решать задачи по темам, пройденным в курсе планиметрии в 7-9 классах. Этот урок мы посвятим четырехугольникам.
Вспомним, какие виды четырехугольников мы выделили, и перечислим основные свойства каждой группы.
Про произвольный четырехугольник(см. рис. 1) мы знаем, что сумма его углов равна 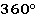 (можно разбить его на два треугольника), и, в отличие от треугольника, у него есть две диагонали (см. рис. 2).
(можно разбить его на два треугольника), и, в отличие от треугольника, у него есть две диагонали (см. рис. 2).
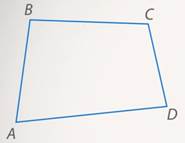
Рис. 1. Произвольный четырехугольник
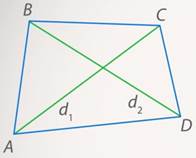
Рис. 2. Диагонали произвольного четырехугольника
Также мы выводили формулу для вычисления площади произвольного четырехугольника через длины его диагоналей и угол между ними:
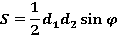
Трапеция
Если в четырехугольнике одна пара сторон параллельна (а другая – нет), то такой четырехугольник называется трапецией (см. рис. 3) (от греческого слова, означающего столик; еще трапецией называется снаряд у гимнастов в цирке – глядя на фото, можете понять, почему (см. рис. 4)).
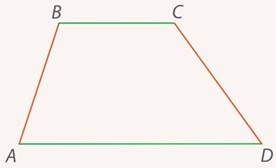
Рис. 3. Трапеция

Рис. 4. Трапеция в гимнастике
За счет запрета параллельности двух боковых сторон трапеция по своим свойствам часто больше напоминает треугольник, чем четырехугольник. Мы у нее вводим среднюю линию(см. рис. 5), свойства которой очень близки к свойствам средней линии треугольника (средняя линия трапеция параллельна основаниям и равна их полусумме).
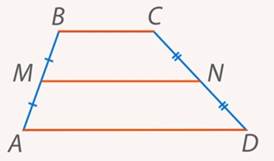
Рис. 5. Отрезок 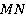 – средняя линия трапеции
– средняя линия трапеции 
Если боковые стороны равны, то трапецию мы называем равнобедренной(см. рис. 6). Углы при основании такой трапеции равны, как и в равнобедренном треугольнике.
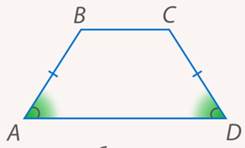
Рис. 6. Равнобедренная трапеция
Если в трапеции один из углов прямой, то несложно доказать, что соседний с ним угол также будет прямым, и такую трапецию мы называем прямоугольной(см. рис. 7).
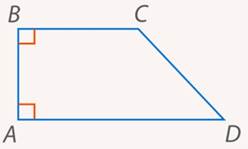
Рис. 7. Прямоугольная трапеция
Параллелограмм
Если добавить к параллельности одной пары противоположных сторон требование параллельности другой пары, то получим четырехугольник, который назвали параллелограммом(см. рис. 8).
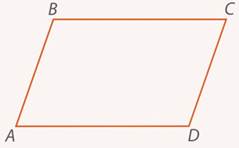
Рис. 8. Параллелограмм
Кроме параллельности противоположных сторон по определению, параллелограмм обладает целым набором свойств.
1. Противоположные стороны не только равны, но и параллельны.
2. Противоположные углы равны, а соседние дают в сумме 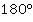 .
.
3. Диагонали точкой пересечения делятся пополам.
4. Площадь равна произведению основания на высоту.
Подвиды параллелограмма
Выделяют и изучают также часто встречающиеся подвиды параллелограмма.
1. Ромб– параллелограмм, у которого все стороны равны (см. рис. 9). У ромба, помимо всех свойств параллелограмма, есть свои собственные: его диагонали перпендикулярны и являются биссектрисами углов ромба.
2. Прямоугольник – параллелограмм, у которого равны все углы (понятно, что тогда все они будут прямыми) (см. рис. 10). Кроме свойств параллелограмма, у прямоугольника еще равны диагонали.
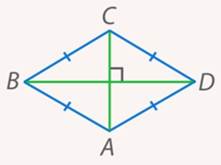
Рис. 9. Ромб
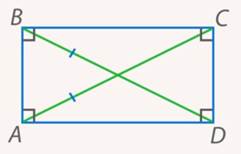
Рис. 10. Прямоугольник
Если же рассмотреть параллелограмм, у которого равны и все стороны, и все углы, то получится четырехугольник, который мы называем квадратом(см. рис. 11). Квадрат является не только параллелограммом, но и ромбом, и прямоугольником.
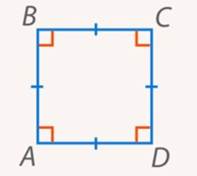
Рис. 11. Квадрат
Теперь мы можем еще раз вспомнить классификацию четырехугольников (см. рис. 12).

Рис. 12. Классификация четырехугольников
Задачи на параллелограмм
Задача 1.Дан параллелограмм  . Проведем его диагональ
. Проведем его диагональ 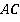 . Построим две биссектрисы
. Построим две биссектрисы 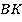 и
и 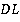 . Построим отрезки
. Построим отрезки  и
и 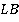 . Является ли полученный четырехугольника
. Является ли полученный четырехугольника 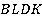 параллелограммом (см. рис. 13)?
параллелограммом (см. рис. 13)?
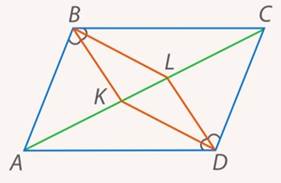
Рис. 13. Иллюстрация к задаче 1
Решение
Внешне он в самом деле похож на параллелограмм. Попробуем это доказать.
Для начала вспомним, как расположены биссектрисы параллелограмма, проведенные из противоположных вершин. Они параллельны – такую задачу мы решали в 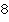 классе:
классе:  (как биссектрисы противоположных углов параллелограмма).
(как биссектрисы противоположных углов параллелограмма).
Параллельности двух сторон нам не хватит. Другие две стороны, к сожалению, не являются биссектрисами, поэтому мы не можем указать на их параллельность.
Рассмотрим два закрашенных треугольника 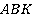 и
и 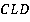 (см. рис. 14).
(см. рис. 14).
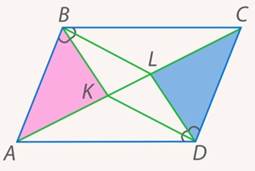
Рис. 14. Иллюстрация к задаче 1
В треугольниках 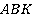 и
и 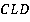 :
:
1. 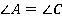 (как внутренние накрест лежащие при параллельных прямых
(как внутренние накрест лежащие при параллельных прямых 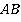 и
и 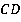 ).
).
2.  (как половины равных друг другу противоположных углов параллелограмма).
(как половины равных друг другу противоположных углов параллелограмма).
3. Стороны 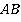 и
и 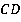 равны как противоположные стороны параллелограмма.
равны как противоположные стороны параллелограмма.
Треугольники 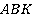 и
и 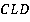 равны по второму признаку (сторона и два угла).
равны по второму признаку (сторона и два угла).
Но тогда отрезки 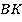 и
и 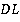 не только параллельны, но и равны друг другу. А это уже признак параллелограмма:
не только параллельны, но и равны друг другу. А это уже признак параллелограмма:
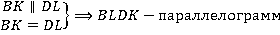
Итак, полученный четырехугольник 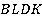 в самом деле параллелограмм.
в самом деле параллелограмм.
Задача 2.Биссектрисы  и
и 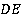 двух углов параллелограмма, прилежащих к одной из его сторон
двух углов параллелограмма, прилежащих к одной из его сторон 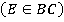 , пересекаются на противоположной стороне. Каким соотношением связаны между собой стороны данного параллелограмма:
, пересекаются на противоположной стороне. Каким соотношением связаны между собой стороны данного параллелограмма: 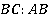 (см. рис. 15)?
(см. рис. 15)?
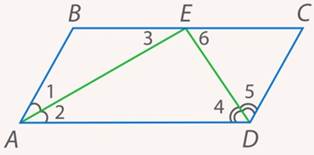
Рис. 15. Иллюстрация к задаче 2
Решение
Итак, пусть биссектрисы пересекаются в точке  на стороне
на стороне 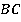 . Мы уже знаем, что такие биссектрисы перпендикулярны друг другу (сумма соседних углов параллелограмма равна
. Мы уже знаем, что такие биссектрисы перпендикулярны друг другу (сумма соседних углов параллелограмма равна 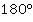 , значит, сумма их половин – углов
, значит, сумма их половин – углов 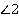 и
и 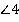 – равна
– равна 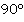 ). Но это в данном случае нас не очень интересует.
). Но это в данном случае нас не очень интересует.
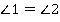 , т. к.
, т. к.  – биссектриса,
– биссектриса, 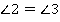 как внутренние накрест лежащие при параллельных, тогда
как внутренние накрест лежащие при параллельных, тогда 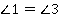 . Тогда треугольник
. Тогда треугольник 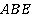 равнобедренный и, следовательно,
равнобедренный и, следовательно, 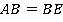 .
.
Аналогично 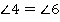 и
и 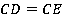 . Но
. Но 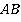 и
и 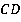 – противоположные равные стороны параллелограмма. Значит, все
– противоположные равные стороны параллелограмма. Значит, все 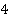 отрезка равны друг другу и сторона
отрезка равны друг другу и сторона 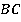 в два раза длиннее стороны
в два раза длиннее стороны 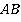 :
: 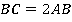 Дополнительно мы доказали, что биссектрисы пересекаются не просто на стороне
Дополнительно мы доказали, что биссектрисы пересекаются не просто на стороне 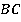 , а на ее середине.
, а на ее середине.
Ответ: 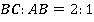 .
.
Задача 3.Дано:  – параллелограмм,
– параллелограмм,  – центр параллелограмма,
– центр параллелограмма, 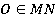 . Доказать, что любая прямая, проходящая через центр параллелограмма, делит его на две равные части (см. рис. 16).
. Доказать, что любая прямая, проходящая через центр параллелограмма, делит его на две равные части (см. рис. 16).
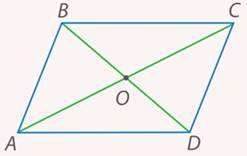
Рис. 16. Иллюстрация к задаче 3
Доказательство
Центром параллелограмма мы называем точку пересечения его диагоналей. Прямая может совпасть с одной из диагоналей. Но мы уже знаем, что диагонали делят параллелограмм на 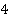 треугольника, которые попарно равны (см. рис. 17). Это легко показать, используя первый признак равенства (по двум сторонам – половинам диагоналей и вертикальным углам между ними):
треугольника, которые попарно равны (см. рис. 17). Это легко показать, используя первый признак равенства (по двум сторонам – половинам диагоналей и вертикальным углам между ними):
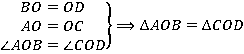
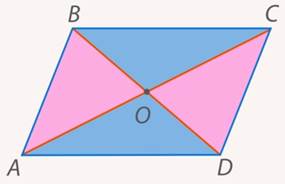
Рис. 17. Иллюстрация к задаче 3
Также легко увидеть, что соседние треугольники хоть и не равны, но все же равновелики. В самом деле, почему площади треугольников 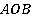 и
и 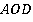 равны?
равны?
Высота большого треугольника 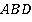 , проведенная из вершины
, проведенная из вершины 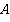 , является высотой для обоих этих треугольников. Их основания
, является высотой для обоих этих треугольников. Их основания 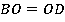 . Следовательно, равны и их площади:
. Следовательно, равны и их площади:
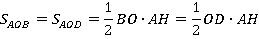
Итак, каждая из диагоналей делит параллелограмм на две равные части. Рассмотрим теперь произвольную прямую 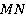 , проходящую через центр параллелограмма (см. рис. 18).
, проходящую через центр параллелограмма (см. рис. 18).

Рис. 18. Иллюстрация к задаче 3
Она разделила параллелограмм на две части (можно даже сказать строже – на две трапеции; подумайте, почему это так), каждая из которых состоит из трех треугольников.
Мы уже обсудили, что треугольники, отсекаемые диагоналями, равны, т. е. 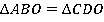 .
.
Покажем равенство треугольников в двух остальных парах (см. рис. 19).
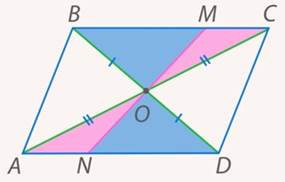
Рис. 19. Иллюстрация к задаче 3
Рассмотрим закрашенную пару треугольников 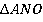 и
и 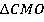 . Они равны по второму признаку равенства:
. Они равны по второму признаку равенства:
1. 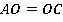 (половины диагонали);
(половины диагонали);
2. 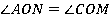 (как вертикальные углы);
(как вертикальные углы);
3. 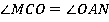 (как внутренние накрест лежащие).
(как внутренние накрест лежащие).
Аналогично равны и два треугольника из оставшейся пары 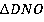 и
и 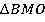 . Так как равные части уложены в одинаковом порядке, то сложенные из них фигуры равны:
. Так как равные части уложены в одинаковом порядке, то сложенные из них фигуры равны:
1. 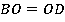 (половины диагонали);
(половины диагонали);
2. 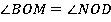 (как вертикальные углы);
(как вертикальные углы);
3. 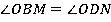 (как внутренние накрест лежащие).
(как внутренние накрест лежащие).
Пожалуй самый важный вывод, который можно сделать из этой задачи: для любой такой прямой отрезки 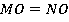 . А это означает, что у каждой точки параллелограмма есть образ, симметричный относительно
. А это означает, что у каждой точки параллелограмма есть образ, симметричный относительно  . Т. е.
. Т. е.  – центр симметрии параллелограмма.
– центр симметрии параллелограмма.
Доказано.
Задача 4.В параллелограмме вырезали дырку прямоугольной формы (см. рис. 20). Провести прямую, делящую оставшуюся часть параллелограмма на две равновеликие части.
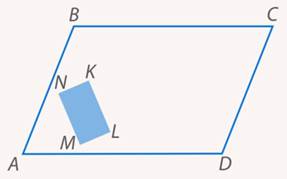
Рис. 20. Иллюстрация к задаче 4
Доказательство
Бывают такие формулировки задач, которые обескураживают. «Да нам же ничего не известно! Как тут решать?»
В самом деле, у нас произвольный параллелограмм. В нем вырезана дыра прямоугольной формы произвольных расположения и размеров. Оставшаяся часть совсем не симметрична. Как же ее разделить на две части равной площади? Как ни странно, но часто именно такие задачи имеют почти мгновенное решение.
Если фигуру можно представить в виде объединения или разности двух фигур, то деление ее на две равновеликие части сводится к делению на такие части каждой фигуры по отдельности.
Таким образом, упростим задачу. Как разделить параллелограмм на две равновеликие части? Только что решенная задача отвечает на этот вопрос: провести любую прямую через центр симметрии. То же самое касается и прямоугольника (см. рис. 21).
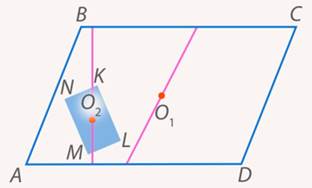
Рис. 21. Иллюстрация к задаче 4
Таким образом, нам нужна прямая, проходящая через оба центра симметрии. Построим эти центры как точки пересечения диагоналей:
 – центр симметрии
– центр симметрии  ;
;
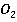 – центр симметрии
– центр симметрии  .
.
Проведем через эти центры прямую (см. рис. 22). Задача решена:
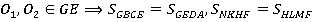
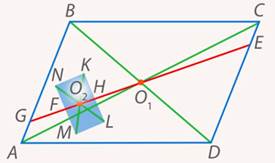
Рис. 22. Иллюстрация к задаче 4
В самом деле, из двух равных частей параллелограмма теперь вырезаны равные части прямоугольника. Оставшиеся части, конечно, тоже равны (см. рис. 23).
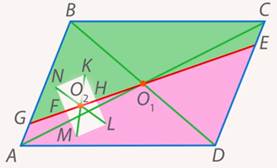
Рис. 23. Иллюстрация к задаче 4
Ответ: прямая 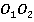 , которая проходит через центры параллелограмма и прямоугольника.
, которая проходит через центры параллелограмма и прямоугольника.
Задачи на трапецию
Задача 5.Дано:  – трапеция,
– трапеция, 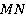 – средняя линия,
– средняя линия, 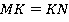 ,
,  .
.
Прямая проходит через середину средней линии трапеции и пересекает основания. Сравнить площади частей 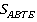 и
и 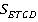 , на которые она разбивает трапецию (см. рис. 24).
, на которые она разбивает трапецию (см. рис. 24).
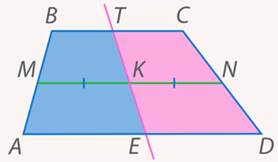
Рис. 24. Иллюстрация к задаче 5
Решение
Прямая делит трапецию на две трапеции 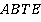 и
и 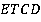 . Мы не знаем длин их оснований. Но чтобы найти площадь трапеции, достаточно знать полусумму оснований, а не каждое основание в отдельности. А эта полусумма как раз равна длине средней линии трапеции:
. Мы не знаем длин их оснований. Но чтобы найти площадь трапеции, достаточно знать полусумму оснований, а не каждое основание в отдельности. А эта полусумма как раз равна длине средней линии трапеции:
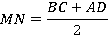
Иными словами, формулу площади трапеции можно воспринимать так: произведение длины средней линии на высоту (см. рис. 25):
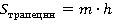
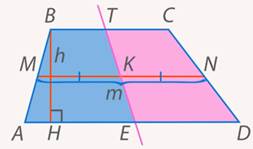
Рис. 25. Иллюстрация к задаче 5
Но средние линии у двух полученных трапеций равны по условию (если параллельные прямые отсекают на одной стороне угла равные отрезки, то равными будут и отрезки на второй стороне угла – теорема Фалеса; значит, линия, которая является средней для большой трапеции, будет таковой и для обеих маленьких трапеций), высота общая. Следовательно, они имеют равную площадь, т. е. равновелики. Похожее свойство мы получили ранее для параллелограмма, но там оно было сильнее. Части были не просто равновеликие (с равными площадями), но и равные.
Ответ: 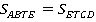 .
.
Задача 6.Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найти углы трапеции (см. рис. 26).

Рис. 26. Иллюстрация к задаче 6
Решение
Отметим у трапеции равные стороны и прямой угол между диагональю и стороной (см. рис. 27).
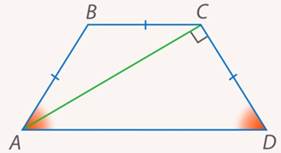
Рис. 27. Иллюстрация к задаче 6
У равнобедренной трапеции углы при основании равны. Обозначим:
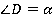
Тогда:
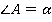
Используя свойство внутренних односторонних углов при параллельных основаниях трапеции, получаем:
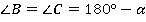
Что нам еще известно? Верхний треугольник  равнобедренный, следовательно, углы при его основании равны. А так как в сумме все три угла должны дать
равнобедренный, следовательно, углы при его основании равны. А так как в сумме все три угла должны дать 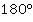 , то углы при основании этого треугольника равны:
, то углы при основании этого треугольника равны:
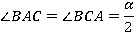
В нижнем треугольнике мы знаем два угла: 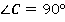 ,
, 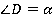 . Значит, оставшийся угол равен:
. Значит, оставшийся угол равен:
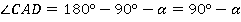
Но тогда угол 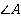 можно выразить двумя способами:
можно выразить двумя способами:
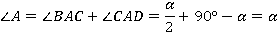
Решаем полученное уравнение:
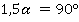

И угол трапеции равен:
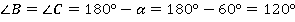
Ответ: 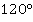 .
.
Задача 7.Может ли средняя линия трапеции проходить через точку пересечения диагоналей (см. рис. 28)?
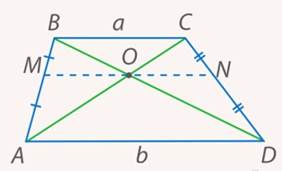
Рис. 28. Иллюстрация к задаче 7
Решение
Предположим, что это возможно и средняя линия трапеции прошла через точку пересечения ее диагоналей. Тогда, по теореме Фалеса, точка пересечения диагоналей и средней линии будет серединой каждой диагонали:  – середина
– середина 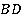 и
и 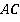 (параллельные прямые, которые отсекают на одной из сторон угла равные отрезки, отсекут равные отрезки и на второй стороне угла).
(параллельные прямые, которые отсекают на одной из сторон угла равные отрезки, отсекут равные отрезки и на второй стороне угла).
Но тогда каждая из двух частей, на которые разделилась средняя линия трапеции, является средней линией треугольника с основанием 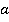 , то есть каждая часть равна
, то есть каждая часть равна  , а сама средняя линия трапеции равна
, а сама средняя линия трапеции равна 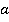 , то есть меньшему основанию:
, то есть меньшему основанию:

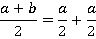
Но мы знаем, что это не так, что средняя линия больше малого основания и равна среднему арифметическому малого и большого основания. Чтобы 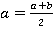 , необходимо, чтобы
, необходимо, чтобы 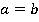 , то есть трапеция была параллелограммом, а мы условились считать, что параллелограмм не является частным случаем трапеции. Таким образом, данная ситуация для трапеции невозможна.
, то есть трапеция была параллелограммом, а мы условились считать, что параллелограмм не является частным случаем трапеции. Таким образом, данная ситуация для трапеции невозможна.
Более того, мы в уроке восьмого класса доказали, что расстояние между серединами диагоналей трапеции равно полуразности оснований, что не равно нулю, так как основания не равны друг другу.
Ответ: нет.
Задача 8.Разрезать прямоугольный равнобедренный треугольник на две такие части, из которых можно сложить квадрат (см. рис. 29).
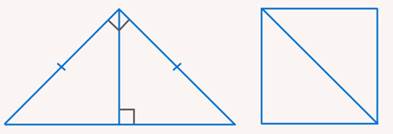
Рис. 29. Иллюстрация к задаче 8
Решение
Задача похожа на головоломки, которые решают перебором вариантов. Так как данная головоломка совсем не сложная, то, может быть, вы сразу нашли ее решение. Вопрос в том, можем ли мы применить какой-то анализ, использовать наши знания по планиметрии.
Порассуждаем. При разрезании фигуры и складывании из частей другой фигуры точно не меняется площадь. Т. е. полученный квадрат должен быть равен по площади данному треугольнику:
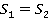
Если сторона треугольника 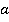 , то площадь равна:
, то площадь равна:
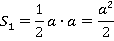
Корень из этой величины даст нам сторону квадрата 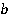 :
:
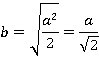
Диагональ квадрата в 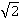 раз больше его стороны:
раз больше его стороны:
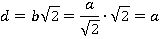
То есть диагональ квадрата равна 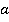 . Но это сторона треугольника.
. Но это сторона треугольника.
Мы поняли, что треугольник нужно разрезать так, чтобы сторона треугольника стала диагональю квадрата. Т.е. на ней, как на гипотенузе, нужно построить другой прямоугольный треугольник. Что и приводит к решению.
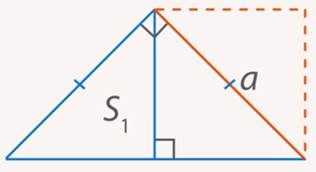
Рис. 30. Иллюстрация к задаче 8
Задачи на подвиды параллелограмма
Задача 9.Прямоугольник  и параллелограмм
и параллелограмм  имеют соответственно равные стороны
имеют соответственно равные стороны 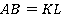 ,
, 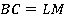 . Найти углы параллелограмма, если его площадь в два раза меньше площади прямоугольника:
. Найти углы параллелограмма, если его площадь в два раза меньше площади прямоугольника: 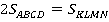 .
.
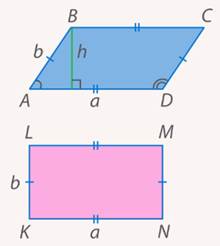
Рис. 31. Иллюстрация к задаче 9
Решение
Из всех параллелограммов самая большая площадь у прямоугольника. Надавливая сверху на параллелограмм, уменьшая его высоту, мы будем уменьшать площадь, сохраняя при этом длины всех сторон. В предельном случае площадь можно уменьшить до нуля.
Для данной задачи удобнее всего нам использовать формулу площади параллелограмма через смежные стороны и синус угла между ними:
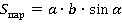
Перепишем условие задачи на математическом языке: половина площади прямоугольника равна площади параллелограмма:
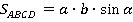

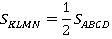
Тогда:
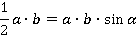

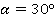
Тогда углы параллелограмма равны 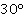 и
и 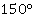 .
.
Ответ: 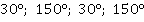 .
.
Задача 10.В треугольнике  через точку пересечения его медиан
через точку пересечения его медиан  проведены отрезки, параллельные сторонам треугольника:
проведены отрезки, параллельные сторонам треугольника: 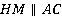 ,
, 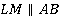 ,
, 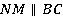 (см. рис. 32). Доказать, что получившиеся части равновелики:
(см. рис. 32). Доказать, что получившиеся части равновелики: 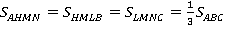 .
.
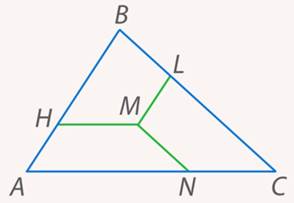
Рис. 32. Иллюстрация к задаче 10
Доказательство
Полученные части – трапеции. Если их площади равны, то каждая из них равна 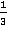 площади всего треугольника:
площади всего треугольника:
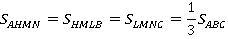
Если мы докажем этот факт для одной трапеции, то он будет верен и для остальных по аналогии. Площадь треугольника равна:
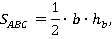
где 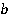 – длина
– длина 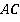 (см. рис. 33).
(см. рис. 33).
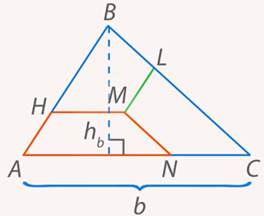
Рис. 33. Иллюстрация к задаче 10
Рассмотрим одну из полученных трапеций и попробуем определить ее основания и высоту для вычисления ее площади. Вспомним, что медианы точкой пересечения делятся в отношении 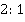 , считая от вершины, тогда для трапеции
, считая от вершины, тогда для трапеции 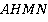 :
:
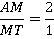
Проведя медиану из вершины 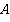 , мы получаем (по обобщенной теореме Фалеса), что нижнее основание трапеции равно (см. рис. 34):
, мы получаем (по обобщенной теореме Фалеса), что нижнее основание трапеции равно (см. рис. 34):
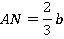
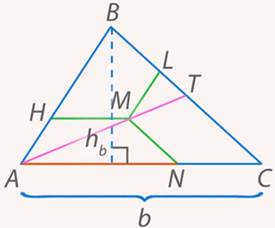
Рис. 34. Иллюстрация к задаче 10
Проведем теперь медиану из точки 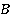 (см. рис. 35). Получим два подобных треугольника
(см. рис. 35). Получим два подобных треугольника 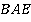 и
и 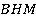 :
:
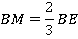
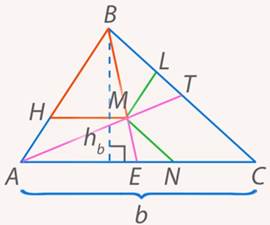
Рис. 35. Иллюстрация к задаче 10
Т. е. это коэффициент подобия. Тогда:
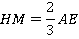
А это половина 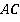 :
:
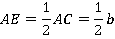
Тогда верхнее основание трапеции 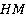 равно:
равно:
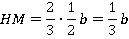
Высота трапеции равна трети высоты треугольника:
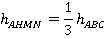
Это следует из подобия треугольников или теоремы Фалеса.
Итак, в рассматриваемой трапеции:
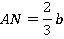
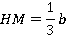
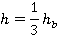
Найдем ее площадь:
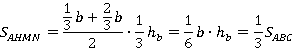
Итак, площадь трапеции равна трети площади треугольника. Аналогично площади остальных двух трапеций равны этой же величине, т. е. равны друг другу.
Доказано.
Задача 11.Найти площадь ромба  , если его высота равна
, если его высота равна 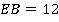 , а меньшая диагональ
, а меньшая диагональ 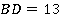 (см. рис. 36).
(см. рис. 36).
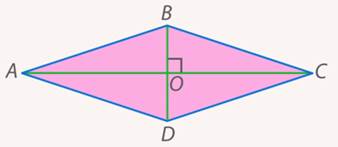
Рис. 36. Иллюстрация к задаче 11
Решение
Проведем высоту из той же вершины, из которой проведена меньшая диагональ (см. рис. 37).
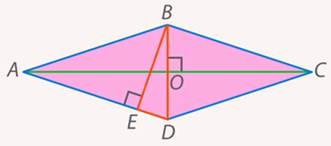
Рис. 37. Иллюстрация к задаче 11
Получили прямоугольный треугольник 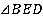 . Нетрудно заметить, что он подобен тем треугольникам, на которые ромб делится диагоналями:
. Нетрудно заметить, что он подобен тем треугольникам, на которые ромб делится диагоналями:
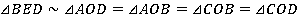
Они тоже прямоугольные, и у них есть равные углы, например 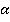 .
.
Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
Можно заняться составлением пропорций, пользуясь подобием треугольников, или сделать то же самое на языке тригонометрических функций.
Для угла 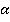 в
в 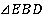 мы знаем гипотенузу и противолежащий катет. Можем найти синус:
мы знаем гипотенузу и противолежащий катет. Можем найти синус:
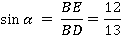
Перейдем к 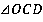 . Мы здесь знаем синус
. Мы здесь знаем синус 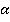 и прилежащий катет
и прилежащий катет 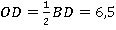 . Чтобы найти второй катет, нам нужен тангенс, а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Первая формула, которая обычно приходит на ум, – основное тригонометрическое тождество:
. Чтобы найти второй катет, нам нужен тангенс, а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Первая формула, которая обычно приходит на ум, – основное тригонометрическое тождество:
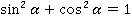
Найдем косинус угла:
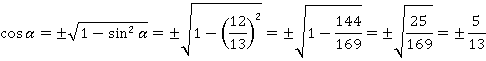
Угол 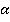 острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти (см. рис. 38).
острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти (см. рис. 38).
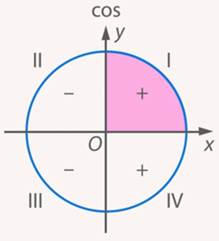
Рис. 38. Иллюстрация к задаче 11
Следовательно, косинус положительный и мы останавливаемся на одном значении:
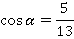
Тогда:
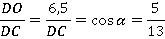
Откуда:
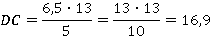
Площадь ромба, как любого параллелограмма, равна произведению основания на высоту:
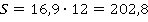
Ответ: 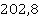 .
.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-портал yaklass.ru (Источник)
2. Интернет-портал math4school.ru (Источник)
3. Интернет-портал youclever.org (Источник)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|