ПРОДОЛЖАЕМ ГОТОВИТЬСЯ К ЭКЗАМЕНУ

5.05 ПРОДОЛЖАЕМ ГОТОВИТЬСЯ К ЭКЗАМЕНУ

ОСНОВНЫЕ ПРАВИЛА:

1. S = pr, где p (полупериметр) = ½ (a + b + c), r – радиус вписанной окружности

2. четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности). В блоке 5 на основе этого свойства доказать, что треугольники подобны.

ОБЯЗАТЕЛЬНЫЕ ЗАДАЧИ :

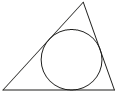4. Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.

4.1

4.2

4.3

4.4

4.5

Задачи 2 части на «5»:

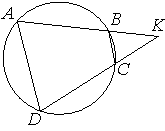5. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.

ВНИМАТЕЛЬНО РАССМОТРИТЕ РЕШЕНИЕ:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB - является смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.
Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD, это мы определили ранее.
Следовательно, данные треугольники подобны (по первому признаку подобия).
Тогда:
BK/DK=BC/AD
AD=(DK*BC)/BK=(12*6)/8=(3*6)/2=3*3=9
Ответ: 9

РЕШАЕМ ЗАДАЧИ ПО АЛГОРИТМУ 5 ЗАДАЧИ)

5.1

5.2

5.3

5.4

5.5

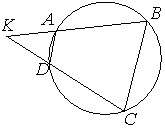5.6

5.7

5.8

5.9