
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Геометрия. 9-а класс.27.05.2020.
Тема урока: Повторение. Скалярное произведение векторов.
На этом уроке мы рассмотрим скалярное произведение векторов и некоторые задачи с его участием.
Вначале вспомним основные сведения про вектор: определение вектора, операции с вектором и угол между векторами. Далее рассмотрим формулу скалярного произведения векторов и рассмотрим важный частный случай перпендикулярных векторов и их скалярное произведение. С помощью формулы скалярного произведения рассмотрим еще два важных частных случая коллинеарных векторов: сонаправленные векторы и противоположно направленные векторы. Дадим определение скалярного квадрата и свойство скалярного квадрата, о равенстве скалярного квадрата квадрату его длины.
Напомним кратко основные сведения, которые мы знаем о векторах.
1. Определение. Вектор – это направленный отрезок, обозначение 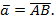
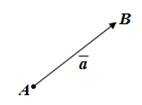
2. Операции с векторами.
а) Сложение векторов.
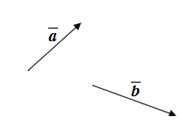
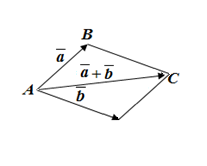
Правило параллелограмма.
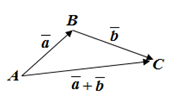
Правило треугольника.
б) Умножение вектора на число.
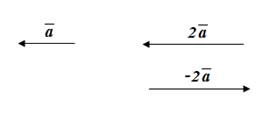
3. Угол между векторами.
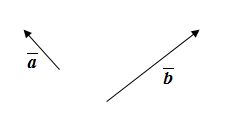
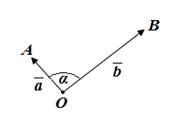
4. Скалярное произведение векторов. 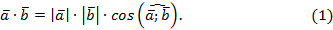
Скалярное произведение векторов – это произведение их длин на косинус угла между ними.
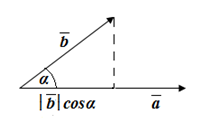
Заметим, что 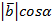 – это проекция вектора
– это проекция вектора 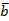 на направление вектора
на направление вектора 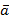 . Из определения следует, что скалярное произведение векторов – это число, характеризующее взаимное расположение векторов.
. Из определения следует, что скалярное произведение векторов – это число, характеризующее взаимное расположение векторов.
Рассмотрим некоторые частные случаи взаимного расположения векторов.
1. Перпендикулярные векторы.
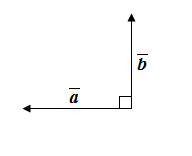
Если 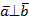 , то
, то 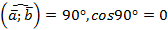 и
и 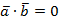 .
.
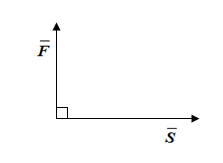
Сила в направлении 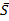 не совершает никакой работы, скалярное произведение
не совершает никакой работы, скалярное произведение 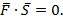 Обратно: если
Обратно: если 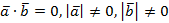 , то
, то 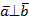 в силу равенства
в силу равенства 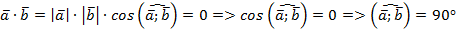 .
.
Получаем следующий важный вывод: Скалярное произведение векторов равно нулю тогда и только тогда, когда векторы перпендикулярны.
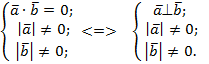
2. Коллинеарные векторы.
Рассмотрим коллинеарные векторы: они могут быть сонаправлены или противоположно направлены.
а) Сонаправленные векторы.
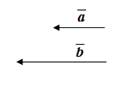
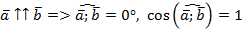 , поэтому
, поэтому 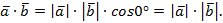 Таким образом,
Таким образом, 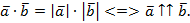
б) Противоположно направленные векторы.
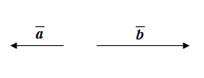
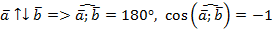 , поэтому
, поэтому 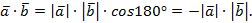
Таким образом, 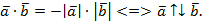
3. Равные векторы. Рассмотрим случай, когда 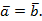
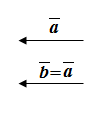
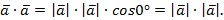
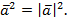
Определение: Скалярное произведение 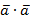 называется скалярным квадратом вектора и обозначается
называется скалярным квадратом вектора и обозначается 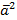 ,
, 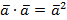 . Свойство: Скалярный квадрат вектора равен квадрату его длины,
. Свойство: Скалярный квадрат вектора равен квадрату его длины, 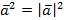 .
.
Следует научиться вычислять скалярное произведение векторов не только в частных, но и в общих случаях. Рассмотрим следующую задачу.
Задача. Вычислить скалярное произведение векторов 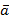 и
и 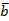 , если
, если 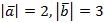 , угол между ними равен:
, угол между ними равен:
а) 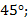
б) 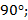
в) 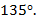
а) Дано: 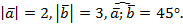
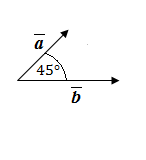
Найти: 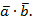 Решение:
Решение: 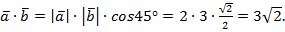 Ответ:
Ответ: 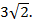
б) Дано: 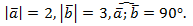
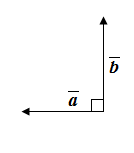
Найти: 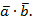 Решение:
Решение: 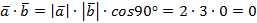 или
или 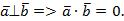 Ответ: 0.
Ответ: 0.
в) Дано: 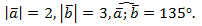
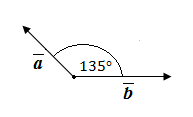

Найти: 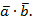
Решение: 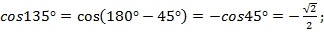
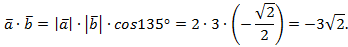 Ответ:
Ответ: 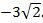
Векторы часто присутствуют и в различных геометрических фигурах. Рассмотрим следующую задачу.
Задача. В равностороннем треугольнике ABC со стороной a проведена высота BD. Вычислить скалярное произведение векторов:
а) 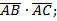
б) 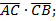
в) 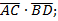
г) 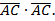
Решение:
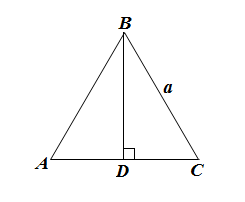
а) 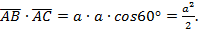 Ответ:
Ответ: 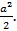
б) Для определения угла между векторами отложим вектор 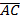 от точки
от точки 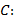
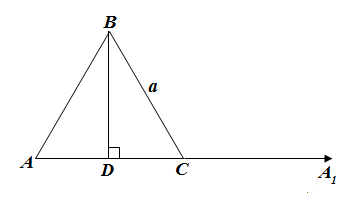
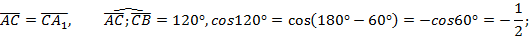
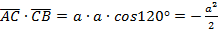 . Ответ:
. Ответ: 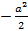 .
.
в) 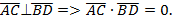 Ответ: 0.
Ответ: 0.
г) 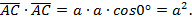 Ответ:
Ответ: 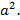
Задача. К одной и той же точке приложены две силы 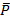 и
и 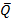 , действующие под углом
, действующие под углом 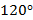 друг к другу, причем
друг к другу, причем 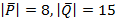 . Найти величину равнодействующей силы
. Найти величину равнодействующей силы 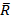 .
.
Дано: 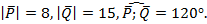
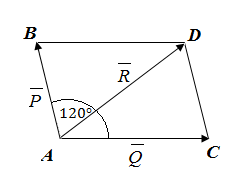
Найти: 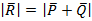 .
.
Решение: 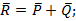
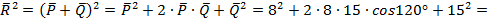
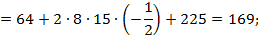
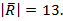
Ответ: 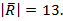
Итак, мы рассмотрели разные задачи на вычисление скалярного произведения векторов.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. E-science.ru (Источник).
2. Mathematics.ru (Источник).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|