Заключение

Геометрия .9-а класс. 15.05.2020.9-б класс.18.05.2020.
Тема урока: Повторение. Треугольники.

На этом уроке мы рассмотрим задачи, для решения которых будем использовать различные факты, касающиеся треугольников.

Средняя линия треугольника

Задача 1. Доказать, что середины сторон равнобедренного треугольника являются вершинами другого равнобедренного треугольника.

Доказательство

Точк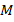и и 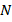разбивают боковые стороны 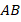и 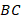на равные отрезки. Но так как сами боковые стороны равны, то все четыре полученных отрезка равны друг другу (см. рис. 1):

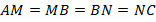
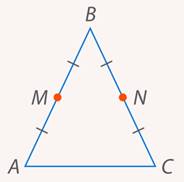
Рис. 1. Иллюстрация к задаче 1

Точка 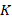разбивает основание на два равных отрезка: 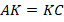. Построим треугольник с этими вершинами (см. рис. 2).

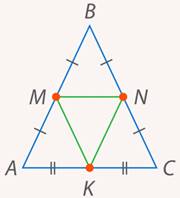
Рис. 2. Иллюстрация к задаче 1

Чтобы показать, что он равнобедренный, можно указать, что равны его стороны: 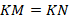. Стандартный способ показать, что два отрезка равны, – это доказать равенство треугольников, где они являются сторонами.

Углы 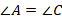, так как большой треугольник равнобедренный. Треугольник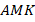и и 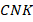равны по первому признаку (две стороны и угол между ними). Следовательно, 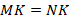, а это значит, что треугольник 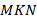равнобедренный (см. рис. 3).

Рис. 3. Иллюстрация к задаче 1

Более простой способ – использовать свойства средней линии: 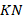, 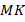– средние линии треугольника, значит, они равны половине соответствующих сторон треугольника:

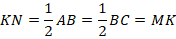
Доказано.

Признак равнобедренного треугольника

Задача 2.Доказать, что если в треугольнике биссектриса и медиана совпадают, то он равнобедренный.

Доказательство

Это один из признаков равнобедренного треугольника. Не надо его путать со свойством: в равнобедренном треугольнике биссектриса и медиана, проведенные к основанию, совпадают.

Признак является обратной теоремой по отношению к свойству. И выполнение одного утверждения далеко не всегда ведет к выполнению обратного. Но в данном случае это так, они выполняются оба. Докажем признак.

Итак, дан треугольник 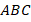. Отрезок 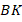является и биссектрисой, и медианой (см. рис. 4). Необходимо доказать, что треугольник равнобедренный, то есть .

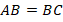Рис. 4. Иллюстрация к задаче 2

Понятно, что хочется показать равенство двух треугольников 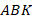и 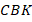. Тогда на этом доказательство будет закончено.

Посмотрим, что у нас есть для этого: 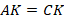, сторона 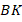общая, 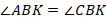. Хотя у нас три элемента одного треугольника равны трем элементам другого, этого недостаточно для их равенства, так как равные углы не находятся между равными сторонами.

Отвлечемся от задачи и посмотрим на такой рисунок (см. рис. 5).

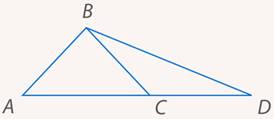
Рис. 5. Иллюстрация к задаче 2

Если основание равнобедренного треугольника 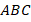продлить и провести еще один отрезок 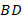, то мы получим два треугольника, 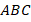и 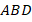, у которых равны две пары сторон и один угол ( 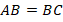, 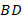общая, общий), но, очевидно, они не равны друг другу хотя бы потому, что один является частью другого. То есть равенства двух сторон и углов, который не лежит между ними, недостаточно, чтобы утверждать, что треугольники равны.

Вернемся к нашей задаче. Продлим 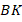вниз и отложим равный ему отрезок 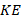. С треугольникам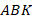и и 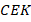ситуация стала проще. Они равны по первому признаку, так как равные углы (вертикальные) находятся теперь между равными сторонами (см. рис. 6):

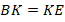
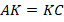
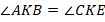
Рис. 6. Иллюстрация к задаче 2

Следовательно:

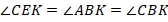
Рассмотрим теперь треугольник 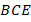(см. рис. 7).

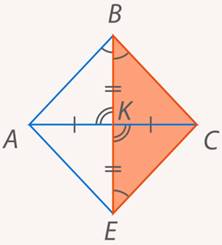
Рис. 7. Иллюстрация к задаче 2

У него равны два угла, значит, он является равнобедренным, следовательно:

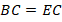
Но так как 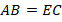, то 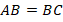, т. е. треугольник 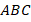равнобедренный.

Доказано.

Высота, проведенная к гипотенузе

Задача 3.Катеты прямоугольного треугольника относятся как 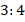, а гипотенуза равна 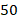. Найти отрезки, на которые гипотенуза делится высотой, и саму высоту (см. рис. 8).

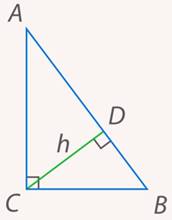
Рис. 8. Иллюстрация к задаче 3

Решение

Начнем с самого треугольника. Нам известно отношение катетов: 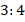. Кроме того мы знаем, что у египетского треугольника стороны относятся как 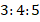(см. рис. 9). Следует ли отсюда, что мы как раз с таким треугольником имеем дело? Да, конечно.

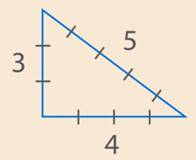
Рис. 9. Иллюстрация к задаче 3

Обозначим длины катетов:

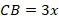
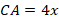
Тогда по теореме Пифагора:

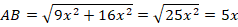
Таким образом, стороны треугольника в самом деле относятся как .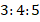

Найдем длины катетов:

Откуда:

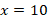
Тогда:

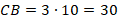
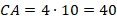
Следующий факт, который нам нужен: высота, проведенная к гипотенузе, делит прямоугольный треугольник на два треугольника, подобных исходному, а следовательно, и друг другу. Увидеть, почему так, совсем не сложно.

Например, треугольники и 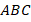имеют равные прямые углы и общий 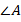. Следовательно, третьи углы у них тоже равны. Треугольники, у которых все три угла одного равны трем углам другого, подобны.

Таким образом, оба малых треугольника тоже являются египетскими, т. е. их стороны относятся как 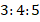. Запишем это отношение для треугольника :

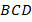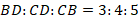
Но 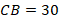, тогда:

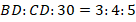
Легче всего в такой ситуации домножить все члены правого отношения на :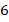

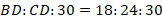
Если один элемент в равенстве совпадает слева и справа, то и остальные тоже:

Аналогично поступим с треугольником :

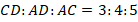
Здесь мы знаем уже два элемента:

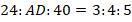
Домножим элементы правого отношения на :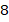

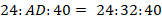
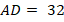
Итак, гипотенуза длиной 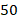делится высотой на отрезк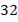и и 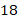, а сама высота равна 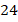(см. рис. 10).

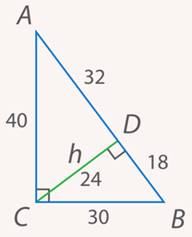
Рис. 10. Иллюстрация к задаче 3

Ответ: 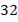и ; .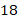

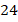Обратите внимание, что:

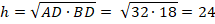
Это неслучайное совпадение. Из того, что треугольники и 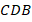подобны треугольнику 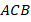, следует, что они подобны друг другу. Но тогда:

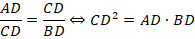
То есть:

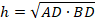
В любом прямоугольном треугольнике высота, проведенная к гипотенузе, равна средним геометрическим проекций его катетов на гипотенузу.

Медианы треугольника

Задача 4.Доказать, что медианы треугольника делят его на шесть треугольников с попарно равными площадями (см. рис. 11).

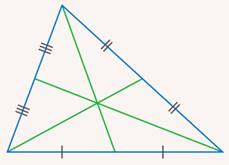
Рис. 11. Иллюстрация к задаче 4

Доказательство

Первый важный факт: все три медианы пересекаются в одной точке. Точка их пересечения – одна из замечательных точек треугольника (центр тяжести треугольника).

Таким образом, исходный треугольник в самом деле делится на 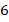треугольников (см. рис. 12).

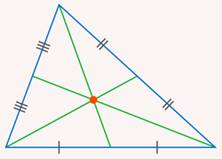
Рис. 12. Иллюстрация к задаче 4

Относительно равенства их площадей задача сводится к более простой. Треугольник делится медианой на два треугольника. У них равны основания и одинаковая высота. Так как площадь треугольника равна половине произведения основания на высоту, эти площади равны (см. рис. 13).

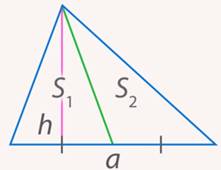
Рис. 13. Иллюстрация к задаче 4

Итак, медиана делит треугольник на два треугольника равной площади. Не путаем: треугольники необязательно равны, равны только их площади. Возвращаемся к нашей задаче. Мы видим, как три треугольника разбиваются своими медианами на пары равных по площади треугольников.

Доказано.

Подобные треугольники

Задача 5.Доказать, что если середины сторон треугольника соединить отрезками, то полученный треугольник будет подобен исходному (см. рис. 14). Найти коэффициент подобия.

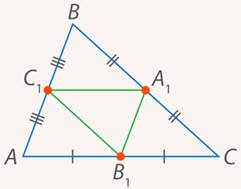
Рис. 14. Иллюстрация к задаче 5

Доказательство

Решение этой задачи основывается на свойствах средней линии треугольника. Вспомним, что средняя линия параллельна основанию треугольника и равна половине этого основания.

Таким образом, маленький треугольник состоит из средних линий большого треугольника. Тогда каждая сторона малого треугольника параллельна стороне большого:

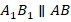
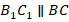
Тогда углы между соответствующими парами параллельных сторон равны:

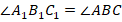
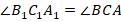
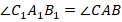
Мы доказали, что треугольник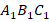и и 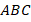подобны. Так как каждая сторона малого треугольника равна половине стороны большого, то периметры относятся как 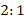. Коэффициент подобия равен .

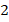Доказано.

Биссектриса угла при основании равнобедренного треугольника

Задача 6.Основание равнобедренного треугольника относится к боковой стороне как 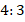, а высота, проведенная к основанию, равна 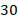. Найти отрезки, на которые эту высоту делит биссектриса угла при основании (см. рис. 15).

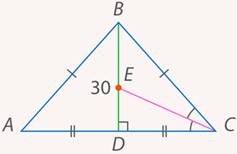
Рис. 15. Иллюстрация к задаче 6

Решение

Обозначим длину основания треугольника 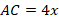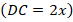, длину боковой стороны . Это и будет означать их отношение .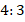

Высота длиной 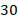делит основание пополам, так как треугольник равнобедренный. Очевидно, мы можем решить полученный прямоугольный треугольник. По теореме Пифагора имеем:

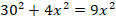
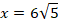
Таким образом, стороны прямоугольного треугольника равны:

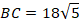
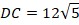
Биссектриса 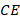делит высоту на два отрезка, длины которых нам и надо найти. Обозначим их пока 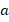и 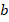(см. рис. 16).

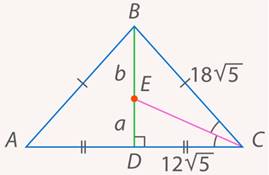
Рис. 16. Иллюстрация к задаче 6

Мы знаем свойства биссектрисы треугольника: она делит противолежащую сторону на отрезки, пропорциональные боковым сторонам. Тогда в треугольнике :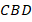

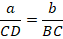
Тогда:

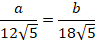
Откуда:

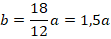
Но:

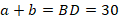
Получаем:

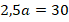
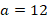
Тогда:

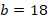
Ответ: .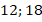

Замечательные точки в треугольнике

Задача 7.Доказать существование четырех точек замечательных в треугольнике.

Доказательство

Вспомним, о чем идет речь. Проведем в треугольнике две биссектрисы. Получим точку их пересечения 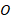(см. рис. 17). Пройдет ли третья биссектриса тоже через точку ?

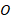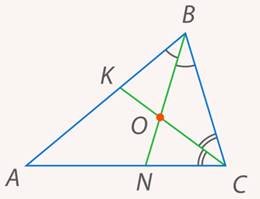
Рис. 17. Иллюстрация к задаче 7

Чтобы ответить на этот вопрос, нужно вспомнить, что биссектриса – это ГМТ, равноудаленных от сторон угла. Т. е. расстояние от любой точки 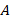на биссектрисе до сторон угла одинаково. В самом деле, опустим перпендикуляры из 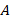на стороны. Получим два прямоугольных треугольника. Эти треугольники равны по гипотенузе (она общая) и острому углу (так как углы 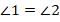равны – определение биссектрисы) (см. рис. 18).

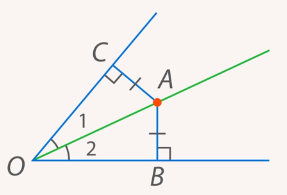
Рис. 18. Иллюстрация к задаче 7

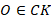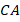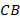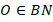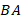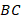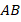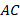Вернемся к биссектрисам треугольника. Точка , следовательно, она равноудалена от и . Точка , следовательно, она равноудалена от и . Значит, она равноудалена от и и 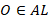. Таким образом, все три биссектрисы проходят через одну точку (см. рис. 19).

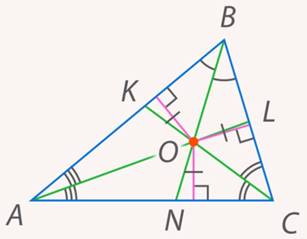
Рис. 19. Иллюстрация к задаче 7

Такое же утверждение верно про пересечение высот, медиан и серединных перпендикуляров. Эти точки и называются четырьмя замечательными точками треугольника. Теорему о точке пересечения биссектрис мы уже доказали. Докажем остальные.

Проведем два серединных перпендикуляра. Получим точку их пересечения (см. рис. 20).

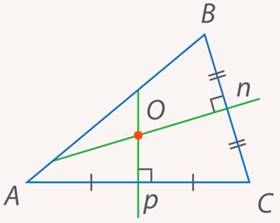
Рис. 20. Иллюстрация к задаче 7

Дальше рассуждения очень похожи на случай биссектрис. Так как точка пересечения 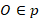, то она равноудалена от вершин 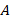и 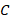(любая точка серединного перпендикуляра равноудалена от концов отрезка, к которому он проведен – докажите это самостоятельно). Она же 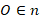, значит, она равноудалена от вершин 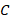и 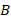. Тогда она равноудалена от вершин 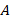и 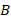, а значит, 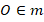. Т. е. все три серединных перпендикуляра пересекаются в одной точке.

Может так произойти, что точка пересечения серединных перпендикуляров лежит вне треугольника (см. рис. 21). Но это никак не влияет на само утверждение. Все три перпендикуляра пересекаются в одной точке.

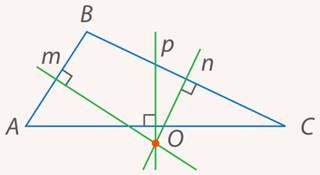
Рис. 21. Иллюстрация к задаче 7

Итак мы доказали существование двух замечательных точек треугольника. Они являются центрами описанной и вписанной окружности (см. рис. 22). Нетрудно разобраться, какая точка какой окружности соответствует.

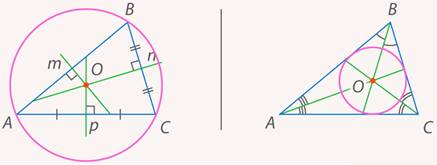
Рис. 22. Иллюстрация к задаче 7

Проведем в треугольнике две высоты. Они пересекутся в точке 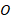(см. рис. 23).

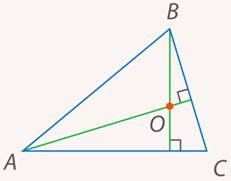
Рис. 23. Иллюстрация к задаче 7

Пройдет ли через точку 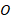третья высота? Сделаем дополнительное построение. Проведем через каждую вершину прямую, параллельную противолежащей стороне треугольника. Получили новый большой треугольник. Зачем он нам? Оказывается, точки 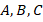являются серединами его сторон (см. рис. 24).

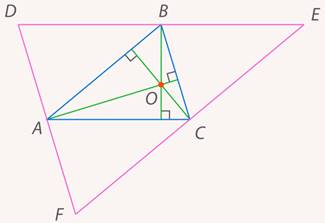
Рис. 24. Иллюстрация к задаче 7

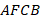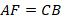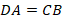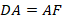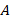В самом деле, посмотрим на четырехугольник . У него противоположные стороны попарно параллельны, следовательно, он параллелограмм. Тогда: . Аналогично: , т. е. и – середина отрезка . Аналогично с остальными точками. Но тогда высоты треугольника являются серединными перпендикулярами треугольника . А они пересекаются в одной точке (см. рис. 25).

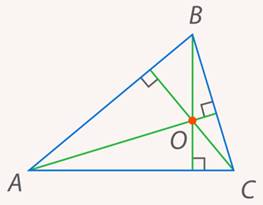
Рис. 25. Иллюстрация к задаче 7

Итак, высоты пересекаются в одной точке. Как и с серединными перпендикулярами, точка пересечения высот может оказаться как внутри, так и за пределами треугольника. В последнем случае говорят не о пересечении самих высоты, а о пересечении их продолжений (см. рис. 26).

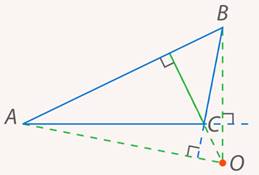
Рис. 26. Иллюстрация к задаче 7

Осталось доказать, что медианы треугольника тоже пересекаются в одной точке. Проведем две медианы треугольника. Они пересекутся в точке 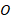(см. рис. 27).

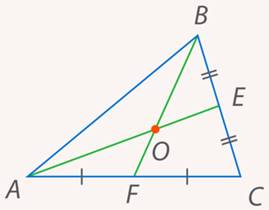
Рис. 27. Иллюстрация к задаче 7

Через середины сторона 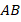и 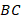проведем прямые, параллельные медиане 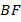(см. рис. 28).

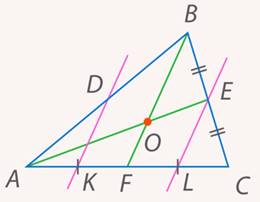
Рис. 28. Иллюстрация к задаче 7

Так как 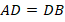, то, по теореме Фалеса:

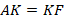
Аналогично, так как 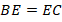, то, по теореме Фалеса:

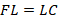
Таким образом:

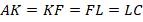
Но тогда, по той же теореме Фалеса, три отрезка, на которые разбита медиана 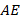, тоже равны друг другу.

Таким образом, мы доказали, что одна медиана отсекает от другой одну треть, если считать от основания (или две трети от вершины). Понятно, что медиана 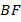тоже разделена в таком же отношении, так как ситуация симметричная. Тогда и последняя, третья, медиана должна отсечь от 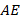треть. Но для этого ей нужно пройти через точку .

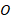Таким образом, все медианы пересекаются в точке и делятся этой точкой в отношении 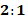(этот факт носит название теоремы Архимеда).

Доказано.

Площадь равностороннего треугольника

Задача 8.Найти площадь равностороннего треугольника со стороной .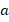

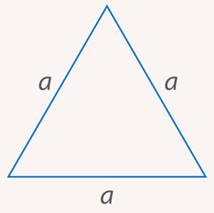
Рис. 29. Иллюстрация к задаче 8

Решение

Задача несложная, но попробуем решить ее, используя разные формулы площади треугольника.

Итак, обычно первая формула, которая приходит на ум, следующая: площадь равна половине произведения основания на высоту:

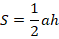
Основание мы знаем, необходимо найти высоту. Найдем ее по теореме Пифагора из прямоугольного треугольника с гипотенузой 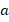и катетом (см. рис. 30):

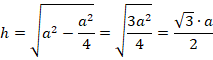
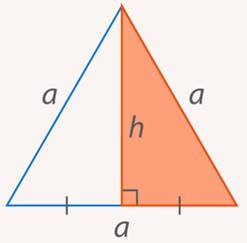
Рис. 30. Иллюстрация к задаче 8

Найдем теперь площадь:

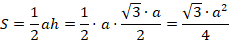
Какой еще формулой мы можем воспользоваться? Мы знаем три стороны треугольника. Следовательно, применима формула Герона:

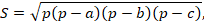
где 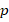– полупериметр:

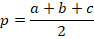
Периметр равен 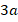, а полупериметр:

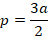
Найдем площадь:

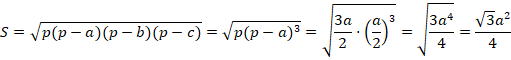
Но все-таки быстрее всего нас к результату приведет формула с синусом, так как, кроме сторон, мы знаем углы, которые все равны по :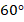

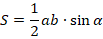
Тогда:

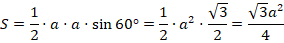
Ответ: .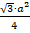

Заключение

Задач, связанных с треугольниками, огромное количество. Какие-то решаются достаточно легко, а какие-то могут быть чрезвычайно сложными. Чтобы хорошо разбираться в геометрии, есть только один путь – решать много задач.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал ru.onlinemschool.com (Источник)

2. Интернет-портал youclever.org (Источник)

3. Интернет-портал ru.solverbook.com (Источник)