
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
г Дата контроля 19.05.20г
14.05.20г Дата контроля 19.05.20г
Тема: Повторение. Многогранники
Задача № 1. Основанием прямой четырехугольной призмы является ромб с диагоналями 1,6 дм и 3 дм, боковое ребро призмы равно 10 дм. Найдите площадь боковой и полной поверхности призмы.
Решение:
И 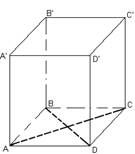 спользуя свойство – диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, найдем сторону .
спользуя свойство – диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, найдем сторону .
OD=0,8 дм, OC=1,5 дм
Рассмотрим ∆СОD- прямоугольный.
CD= 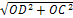
CD= 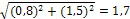 дм
дм
AB=BC=CD=AD=1,7 дм
S=4∙ (1,7∙10)=68 дм2.
Ответ: 68 дм2
Задача № 2. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро - 6 см. Найдите Sсеч, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
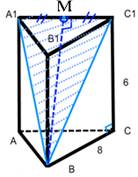
Решение:
Треугольник A1B 1C1 - равнобедренный(A1 B=C1B как диагональ равных граней)
1)Рассмотрим треугольник BCC1– прямоугольный
BC1 2 =BС2 +CC1 2
BC1= 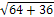 =10 см
=10 см
2) Рассмотрим треугольник BMC1– прямоугольный
BC1 2 = BM2 + M C1 2
BM2 = BC1 2 -M C1 2
BM2 =100-16=84
BM= 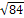 =2
=2 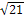 см
см
3) Sсеч =  A1C1 *BM=
A1C1 *BM=  ∙8∙2
∙8∙2 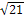 =8
=8 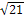 см2
см2
Ответ:8 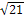 см2
см2
Задача № 3. Основание пирамиды- параллелограмм со сторонами 6 см и 8 см, высота пирамиды- 12 см, а все боковые ребра равны между собой. Найдите длину бокового ребра.
Решение:
1. АО- высота. АС=АВ=АЕ=AD, то DO=OВ=ОС=ОЕ, поэтому точка О- центр окружности описанной около параллелограмма BCDE. Но тогда параллелограмм является параллелограммом, диагонали которого пересекаются в точке О и равны друг другу. BCDE- прямоугольник.
2. Из ∆BDC по теореме Пифагора , DB==10 см., следовательно АО= 5 см
АО  DBC. ∆АОD- прямоугольный, по теореме Пифагора , АD==13 см.
DBC. ∆АОD- прямоугольный, по теореме Пифагора , АD==13 см.
Ответ: 13 см
Задача № 4. Стороны оснований правильной усеченной четырехугольной пирамиды равны 2 м и 8 м. Боковое ребро равно 5 м. Найдите высоту пирамиды.
Решение:
АА1С1 С- равнобокая трапеция. А1С1 и АС- диагонали соответственно верхнего и нижнего основания пирамиды. А1С1=2 см, АС= 8 см (как диагонали квадрата).
Проведем высоты А1Е и С1К. АЕ=КС=(АС- А1С1)/2=(8)/2=3 см.
∆А А1Е- прямоугольный, по теореме Пифагора найдем А1Е.
А1Е=? см.
Ответ: ?см
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|