Рисунок 2. Рисунок 3

Рисунок 2

Допустим четырехмерное пространство – это сфера с четырьмя точками координат создающая пространство за трехмерным, в том числе частью трехмерного пространства.

Если от линии, с точки координат создавшая четырёхмерное пространство, провести линию вниз под углом 45 градусов, и соединить сначала с линией высоты, далее с линий длины, и с линией ширины, то получаем линию, она же точка координат для пятимерного пространства (рисунок 3).

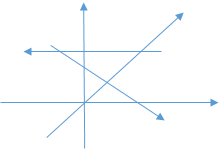
Рисунок 3

Данная точка координат четырехмерного пространства выходя наружу и возвращаясь, соединяет одномоментно трехмерное пространство, создаёт пятимерное пространство.

Сфера в пятимерном пространстве, это примерно так как бы двухмерный круг имел в себе, трёхмерную сферу и/или/ наоборот. Пятимерная сфера, имея четырехмерное пространство, имеет ещё одну точку координат одномоментно во внутрь и на выход сферы. Выход наружу от сферы четырехмерного пространства, в ещё одну точку координат, формирует пятимерное измерение. И тут уже пошло расхождение, так как выражаться трёхмерными определениями о многомерности по моему разумению не возможно. Выглядит примерно так. Сфера с трёхмерного пространства, то есть шар, может быть глубже и длиннее. В одном шаре, и всё сразу одномоментно. Где часть следующего пространства шара чуть больше в объёме, глубине и /или/ по высоте.

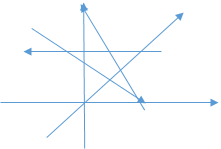
Шестимерное пространство, на том же рисунке – это пятимерное пространство имеющее соединение новой линией сточками координат для шестимерного пространства.

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒