Геометрия.. Решение.

Геометрия.

На экзамене в ответе записываем только число, единицы измерения (см, км и т.д), градусы не записываем, это будет ошибкой.

Пример решения задачи:

В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 2 см. Ответ дайте в кубических сантиметрах.

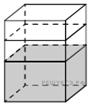
Решение.

Объем вытесненной жидкости равен объему детали (закон Архимеда). Уровень жидкости поднялся на h = 2 см, сторона основания a = 40 см, значит, вытесненный объем будет равен V = а² ·h = 40·40·2 = 3200 см³. Найденный объём является объёмом детали.

Ответ: 3200

Задачи (решить):

1 Задача. В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 20 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.

2 Задача. В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 10 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 30 см. Ответ дайте в кубических сантиметрах.

Пример решения задачи:

В бак, имеющий форму прямой призмы, налито 12 л воды. После полного погружения в воду детали, уровень воды в баке поднялся в 1,5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

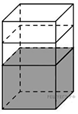
Решение.

Объем детали равен объему вытесненной ею жидкости. После погружения детали в воду объём стал равен 12 · 1,5 = 18 литров, поэтому объём детали равен 18 − 12 = 6 л = 6000 см³.

Ответ: 6000

Задача (решить):

3 Задача. В бак, имеющий форму правильной четырёхугольной призмы, налито 10 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,2 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

Пример решения задачи:

Аквариум имеет форму прямоугольного параллелепипеда с размерами 70 см х 20 см х 60 см. Сколько литров составляет объем аквариума? В одном литре 1000 кубических сантиметров.

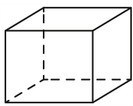
Решение

1. Для решения данной задачи необходимо знать формулу для нахождения объема прямоугольного параллелепипеда:

Объем прямоугольного параллелепипеда равен произведению его высоты на длину и ширину:

V = a · b · h

2. Тогда объем аквариума равен:

V = 70 · 20 · 60 = 84000 см³

3.Переведём объем аквариума из сантиметров кубических в литры (в одном литре тысяча сантиметров кубических):

V = 84000 см³: 1000 = 84 литра объем аквариума

Ответ: 84

Задачи (решить):

4 Задача. Аквариум имеет форму прямоугольного параллелепипеда с размерами 70 см× 20 см ×60 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.

5 Задача. Аквариум имеет форму прямоугольного параллелепипеда с размерами 80 см × 30 см × 40 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.