
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Критические точки функции. Точки максимума и минимума функции
Критические точки функции. Точки максимума и минимума функции
Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называются критическими точками функции.
Если 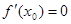 , то х0 – критическая точка функции
, то х0 – критическая точка функции 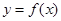 .
.
Необходимое условие экстремума (теорема Ферма). Если точка х0 является точкой экстремума функции 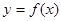 и в этой точке существует производная
и в этой точке существует производная 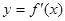 , то она равна нулю.
, то она равна нулю.
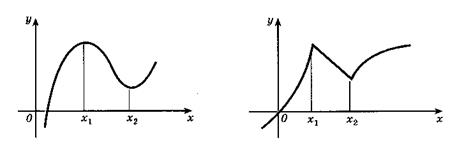
Признак максимума функции. Если функция 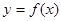 непрерывна в точке х0, а
непрерывна в точке х0, а 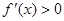 на интервале (а; х0) и
на интервале (а; х0) и 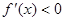 на интервале (х0; b), то точка х0 является точкой максимумафункции
на интервале (х0; b), то точка х0 является точкой максимумафункции 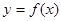 .
.
Удобно пользоваться упрощённой формулировкой этого признака:
Если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума.
Признак минимума функции. Если функция 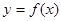 непрерывна в точке х0, а
непрерывна в точке х0, а 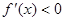 на интервале (а; х0) и
на интервале (а; х0) и 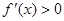 на интервале (х0; b), то точка х0 является точкой минимумафункции
на интервале (х0; b), то точка х0 является точкой минимумафункции 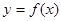 .
.
Удобно пользоваться упрощённой формулировкой этого признака:
Если в точке х0 производная меняет знак с минуса на плюс, то х0 есть точка минимума.
Все точки минимума и точки максимума называются точками экстремума функции.
Пример1.Найти точки экстремума функции 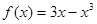 .
.
Решение.
Находим производную функции 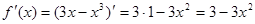 .
.
Находим критические точки функции: 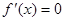 ;
; 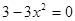 ;
;
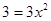 ;
;
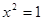 ;
;
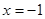 ;
; 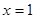 .
.
Находим знак производной при 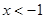 ,
, 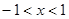 и
и 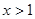 .
.
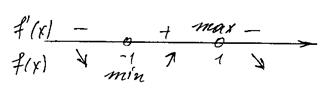
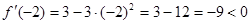 ;
;
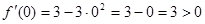 ;
;
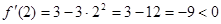 .
.
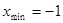 ,
, 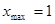 .
.
Ответ: 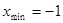 ,
, 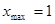 .
.
Домашнее задание.
№ 286. Найдите критические точки функции: а) 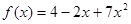 ; г)
; г) 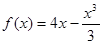 .
.
№ 290. Найдите критические точки функции. Определите, какие из них являются точками максимума, а какие – точками минимума.
а) 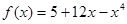 ; б)
; б) 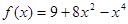 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|