Решение систем линейных уравнений методом подстановки.

15.05. Решение систем линейных уравнений методом подстановки.

Ход занятия: число, тема занятия.

1). Проверка д/з:

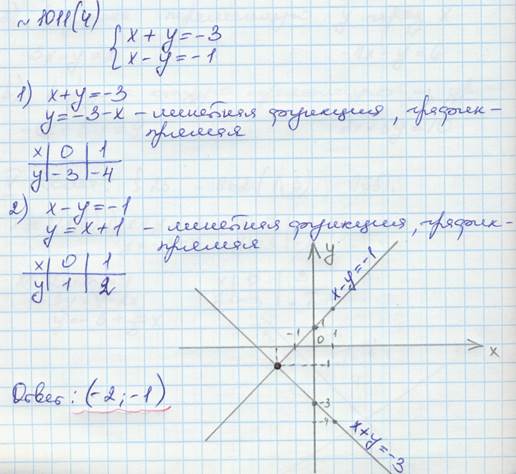
2). Прочитайте #27, внимательно изучите алгоритм решения системы методом подстановки.

Теория.

Алгоритм решения системы двух уравнений с двумя переменными методом подстановки:

1. из любого (обычно более простого) уравнения системы выразить одно неизвестное через другое,

например, x через y из первого уравнения системы;

2. подставить полученное выражение в другое (второе) уравнение системы вместо x;

3. решить уравнение с одним неизвестным относительно y (найти y);

4. подставить найденное на третьем шаге значение y в уравнение,
полученное на первом шаге, вместо y и найти x;

5. записать ответ.

Пример:

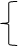Решить систему уравнений:

x−2y=3

5x+y=4 , 1) из первого уравнения системы (x−2y=3), получаем:

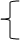x=3+2y

5x+y=4, 2) подставим найденное выражение вместо x во второе уравнение системы:

5⋅(3+2y)+y=4, 3) решим полученное уравнение, найдём y:

15+10y+y=4;

10y+y=4−15;

11y=−11

y=-11:11

у=−1, 4) Подставим найденное значение y в полученное на первом шаге уравнение вместо y и найдём x.

x=3+2⋅y

x=3+2⋅(−1)=3−2 =1 5) запишем ответ

Ответ: (1;−1).

3) Рассмотрим решение систем методом подстановки (все решения записать в тетрадь) №1034(2,4)

2) 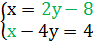, первый пункт алгоритма можно пропустить, переменная х выражена

2у-8-4у=4

2у-4у=4+8

-2у=12

у=12 : (-2)

у=-6

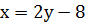
х=2∙(-6)-8=-12-8=-20

Ответ: (-20;-6)

4) 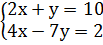, из первого уравнения выразим у через х

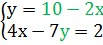, подставим вместо у выражение (10-2х)

4х-7∙(10-2х)=2

4х-70+14х=2

4х+14х=2+70

18х=72

х=72:18

х=4

у=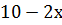

у=10-2∙4=10-8=2

Ответ: (4;2).

Домашнее задание: #27, знать алгоритм решения системы методом подстановки, №1035(2,5). Скинуть в группу.