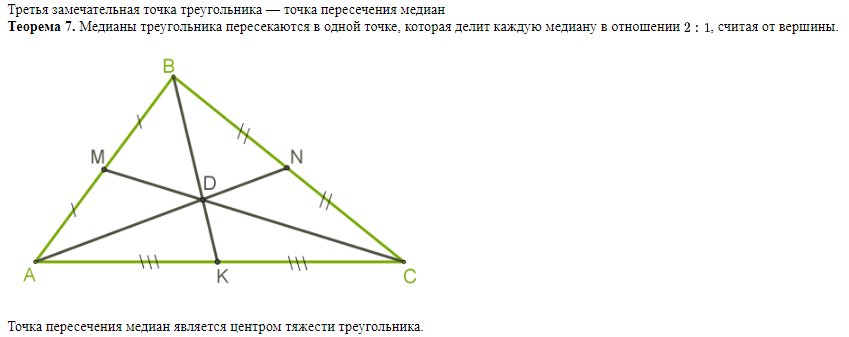
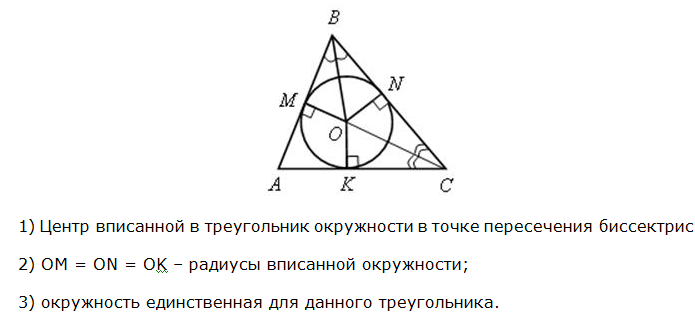
Центр вписанной окружности - точка пересечения биссектрис многоугольника.

Посмотреть видео-урок по ссылке: https://www.youtube.com/watch?v=EBZvlSUjIi4

Записать конспект и выполнить самостоятельную работу!

Центр вписанной окружности - точка пересечения биссектрис многоугольника.

Теорема: В любой треугольник можно вписать окружность, и притом только одну.

Теорема – свойство описанного четырёхугольника:

В любом описанном четырёхугольнике суммы противоположных сторон равны.

Обратное утверждение:

Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность

Формулу для нахождения радиуса вписанной окружности:

Ответить на вопросы и заполнить троеточии:

1. Где находится центр окружности, вписанной в треугольник?

2. От чего равноудален центр описанной около треугольника окружности?

3. Где находится центр окружности, описанной около треугольника?

4. В любой треугольник можно вписать окружность?

5. Если ...стороны многоугольника касаются окружности, то окружность называется …..…….. в многоугольник, а многоугольник – …..…… около этой окружности.

6. Всегда ли можно вписать окружность в треугольник?

7. Всегда ли можно вписать окружность в четырехугольник?

8. В выпуклый четырёхугольник можно вписать окружность только тогда, когда …………………………………………..………………….. . .

9. Окружность называется ………..около многоугольника, если все вершины многоугольника лежат на данной окружности.

10. Многоугольник называется …….……в окружность, если все его вершины лежат на данной окружности.

Домашнее задание: стр.162-182 повторить теоремы ,следствия! Выполнить №693(а),695,702(а), подготовиться к к/р.