
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ВОПРОСЫ К ЭКЗАМЕНУ ПО МАТЕМАТИКЕ
ВОПРОСЫ К ЭКЗАМЕНУ ПО МАТЕМАТИКЕ
для студентов 1 курса группы 3Э-11, 3БД-11, 3Ф-11
Часть А
1. Корень n-ой степени. Свойства корня n-ой степени. Обобщение понятия о показателе степени
2. Понятие логарифма и его свойства. Основное логарифмическое тождество.
3. Десятичные и натуральные логарифмы. Правила действий с логарифмами. Переход к новому основанию.
4. Логарифмические уравнения. Приемы решения. Примеры.
5. Логарифмическая функция. Ее свойства, график.
6. Тригонометрические функции. Определение синуса, косинуса, тангенса, котангенса.
7. Радианная мера угла. Переход от градусной меры к радианной и наоборот.
8. Зависимость между тригонометрическими функциями одного угла.
9. Формулы двойного угла. Формулы сложения.
10. Решение простейших тригонометрических уравнений.
11. Тригонометрические функции. Область определения и множество значений тригонометрических функций.
12. Обратные тригонометрические функции.
13. Основные понятия комбинаторики: размещения, перестановки и сочетания.
14. Теория вероятностей. Событие, вероятность события.
15. Зависимость и независимость событий. Совместность и несовместность событий. Противоположность событий.
16. Теория вероятностей. Сложение и умножение вероятностей.
17. Приращение функции и приращение аргумента. Определение производной.
18. Физический и механический смысл производной.
19. Уравнение касательной к графику функции
20. Правила и формулы дифференцирования.
21. Применение производной для нахождения экстремума функции
22. Понятие интеграла и первообразной
23. Теорема Ньютона – Лейбница
24. Стереометрия. Основные аксиомы стереометрии и следствия из аксиом.
25. Прямые и плоскости в пространстве. Взаимное расположение двух прямых в пространстве.
26. Взаимное расположение прямой и плоскости. Параллельность прямой и плоскости.
27. Взаимное расположение двух плоскостей в пространстве. Перпендикулярность двух плоскостей.
28. Двугранный угол. Угол между плоскостями.
29. Многогранники. Вершины, ребра, грани многогранника. Формула Эйлера.
30. Призма и ее свойства. Прямая и наклонная призмы.
31. Правильная призма. Площадь боковой и полной поверхности призмы.
32. Куб. Параллелепипед и его свойства. Объем куба. Объем параллелепипеда.
33. Пирамида и ее свойства. Площадь боковой и полной поверхности пирамиды.
34. Правильная пирамида. Усеченная пирамида.
35. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
36. Тела и поверхности вращения. Цилиндр. Основания, высота, боковая поверхность, образующая, развертка. Площадь боковой и полной поверхности.
37. Тела и поверхности вращения. Конус. Основание, высота, боковая поверхность, образующая, развертка. Площадь боковой и полной поверхности.
38. Шар и сфера. Площадь поверхности сферы.
39. Сечения шара и сферы.
40. Формулы объема пирамиды, цилиндра и конуса. Формула объема шара.
Часть В
1. Вычислить: 1) 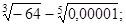 2)
2) 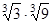 ; 3)
; 3) 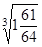
2. Вычислить: 1)  ; 2)
; 2)  ; 3)
; 3) 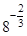 ; 4)
; 4) 
3. Представить бесконечную периодическую дробь в виде обыкновенной: 1) 0,(35); 2) -3,11(5)
4. Представить бесконечную периодическую дробь: 1) -3,11(5); 2) 1,2(31) в виде обыкновенной
5. Даны числа  ,
, 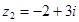 . Найдите числа: а)
. Найдите числа: а)  ; б)
; б)  ; в)
; в) 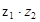 ; г)
; г) 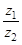 , д) взаимно сопряженные числам
, д) взаимно сопряженные числам 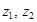 ; е) противоположные числам
; е) противоположные числам 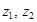 ; ж) модуль комплексных чисел
; ж) модуль комплексных чисел 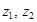
6. Даны числа 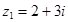 ,
, 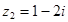 . Найдите числа: а)
. Найдите числа: а)  ; б)
; б)  ; в)
; в) 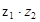 ; г)
; г) 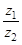 , д) взаимно сопряженные числам
, д) взаимно сопряженные числам 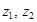 ; е) противоположные числам
; е) противоположные числам 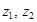 ; ж) модуль комплексных чисел
; ж) модуль комплексных чисел 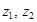
7. Решить уравнение:1)  ; 2)
; 2) 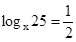
8. Решить уравнение:1)  ; 2)
; 2) 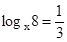
9. Вычислить: 1) 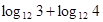 ; 2)
; 2) 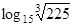
10. Вычислить: 1) 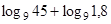 ; 2)
; 2) 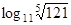
11. Вычислить 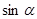 , если
, если 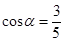 и
и 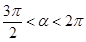
12. Вычислить 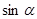 и
и 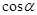 , если
, если  и
и 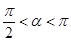
13. Вычислить а) 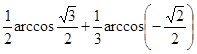 ; б)
; б) 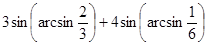
14. Вычислить а) 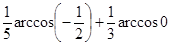 ; б)
; б) 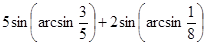
15. Упростить выражение 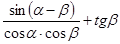
16. Упростить выражение 
17. Решить уравнение 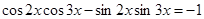
18. Решить уравнение 
19. Решить уравнение 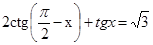
20. Привести уравнение к квадратному относительно одной из тригонометрических функций и найти его корни 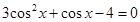
21. Решить уравнение, разложив на множители его левую часть 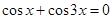
22. Решить уравнение а) 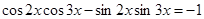 ; б)
; б) 
в) 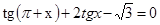
23. Привести уравнение к квадратному относительно одной из тригонометрических функций и найти его корни 
24. Решить уравнение, разложив на множители его левую часть 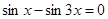
25. Решить уравнение 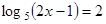
26. Решить уравнение 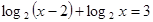
27. Решить уравнение 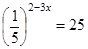
28. Решить уравнение 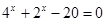
29. Решить уравнение 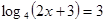
30. Решить уравнение 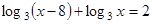
31. Решить уравнение 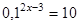
32. Решить уравнение 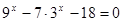
33. Докажите четность (нечетность) функции: 
34. Докажите четность (нечетность) функции 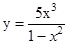
35. Исследуйте функцию и постройте ее график 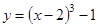
36. Найдите область определения функции: 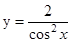
37. Найдите область значений функции: 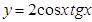
38. В одной системе координат схематически постройте графики функций  и
и 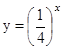
39. Докажите четность (нечетность) функции 
40. Докажите четность (нечетность) функции 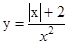
41. Исследуйте функцию и постройте ее график 
42. Найдите область определения функции: 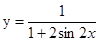
43. Найдите область значений функции: 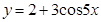 .
.
44. В одной системе координат схематически постройте графики функций  и
и 
45. Найти производную функции y= 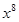 ; y=
; y= 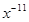 ; y=
; y=  ; y=
; y= 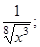 y=
y=  ; y=
; y= 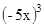
46. Найти  для
для  ;
; 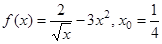
47. Найти производную функции y=  ; y=
; y= 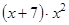 ; y=
; y= 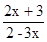
48. Найти производную функции y= 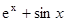 ; y=
; y= 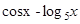 ; y=
; y=  ; y=
; y= 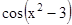
49. Найти промежутки возрастания и убывания функции 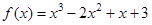
50. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 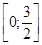
51. Найти производную функции y= 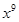 ; y=
; y= 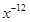 ; y=
; y= 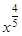 ; y=
; y=  y=
y= 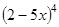 ; y=
; y= 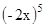
52. Найти  для а)
для а)  ; б)
; б) 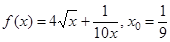
53. Сократить дробь 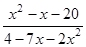
- Найти все первообразные данной функции а)
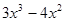 ; б)
; б) 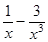 ; в)
; в) 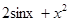 ;
;
г) 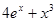
- Найти все первообразные данной функции а)
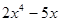 ; б)
; б) 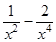 ; в)
; в) 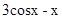 ;
;
г) 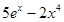
- Найдите cos a и tg a, если sin
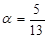 и a - угол II координатной четверти
и a - угол II координатной четверти - Найдите cos a и tg a, если sin a = 0,6 и a - угол I координатной четверти
- Найдите cos a и tg a, если sin a = - 0,8 и a - угол III координатной четверти
- Найдите sin a и tg a, если cos a = 0,6 и a - угол I координатной четверти
- Вычислите интеграл

- Вычислите интеграл
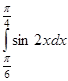 .
. - Вычислите интеграл

- Вычислите интеграл

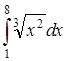
64. Вычислите интеграл 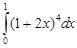
- Для функции f(x) найти первообразную, график которой проходит через точку M.
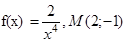
- Для функции f(x) найти первообразную, график которой проходит через точку M.
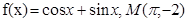 .
.
67. В ящике 20 шаров, из них 12 белых, остальные голубые. Извлекают 2 шара. Найти вероятности, что оба шара белые.
68. В первой урне содержится 8 синих и 10 желтых шаров, во второй 4 белых и 12 желтых шаров. Из каждой урны наудачу извлекли по одному шару. Найти вероятность того, что оба извлеченных шара желтого цвета.
69. В коробке находятся 2 белых, 5 черных и один синий шар. Наугад вынимают один из них. Найти вероятность события: 1) вынут белый шар; 2) вынут черный шар; 3) вынут синий шар; 4) вынут или белый, или черный шар; 5) вынут не черный шар; 6) вынут не белый шар.
70. В коробке 30 синих и 24 красных кубиков. Из коробки вынули сразу 2 кубика. Найдите вероятность того, что эти кубики синие.
71. Вероятность того, что при одном выстреле стрелок попадает в мишень, равна 0,6. Какова вероятность того, что выстрелив по мишени один раз, этот стрелок промахнется?
72. Брошены две игральные кости. Найдите вероятности следующих событий: а) сумма выпавших очков равна 6; б) сумма выпавших очков равна 8, а разность 3.
73. Найти моду, медиану, и среднее выборки: 1) -8, -8, -5, -5, 0, 2; 2) -4, -4, 0, 2, 9, 9.
- Вероятность того, что при одном выстреле стрелок попадает в мишень, равна 0,9. Какова вероятность того, что выстрелив по мишени один раз, этот стрелок промахнется?
- Найти моду, медиану, и среднее выборки: 1) 3, -2; 1; 0; 2; -1; 2) 7, 4, -1, 3, -3, 0.
76. Диагональ осевого сечения цилиндра равна 12 см, а радиус основания – 6 см. Найдите высоту цилиндра.
77. В правильной четырёхугольной пирамиде высота равна 12см, а апофема - 15см. Найдите площадь полной поверхности пирамиды.
78. В основании правильной четырехугольной призмы ABCDA1B1C1D1 лежит квадрат со стороной 4 см. Диагональ призмы AC1 образует с плоскостью основания ABCD угол 60°. Найдите высоту призмы и площадь полной поверхности.
79. Диагональ правильной четырехугольной призмы составляет с боковой гранью угол 60°. Найдите объем призмы, если сторона основания 8см
- Радиусы оснований усеченного конуса равны 12 см и 6 см, а образующая наклонена к плоскости основания под углом 45°. Найдите площадь и объем усеченного конуса.
- Найдите полную площадь поверхности и объем пирамиды, у которой высота равна 2 м, а основанием пирамиды является квадрат со стороной 3 м.
82. Основанием пирамиды является треугольник со сторонами 12 см,10 см,10 см. Каждая боковая грань наклонена к основанию под углом 60°. Найдите объем и площадь боковой поверхности пирамиды.
83. Найдите сторону основания и высоту правильной четырёхугольной призмы, если Sполн=90см2, Sбок=40см2.
84. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра и удаленной на 9 дм от нее, равна 240 дм 2. Найдите радиус цилиндра.
- Основание прямой призмы – равнобедренный треугольник со стороной 6 см, а диагональ боковой грани 10 см. Найдите площадь боковой поверхности и объем призмы.
- В правильной четырехугольной призме площадь основания равна 25 см², а высота 4 см. Найдите диагональ и объем призмы.
- Основанием прямой призмы служит прямоугольный треугольник с катетами 12 см и 5 см, высота призмы равна 8 см. Найдите площадь полной поверхности.
- Радиус окружности, описанной около основания правильной шестиугольной призмы, равен 3 см. Найдите площадь полной поверхности призмы, если её высота равна 10 см.
89. Диагональ правильной четырехугольной призмы составляет с боковой гранью угол 30°. Найдите площадь боковой поверхности и объем призмы, если сторона основания  см.
см.
90. Высота цилиндра на 12 см больше его радиуса, а площадь полной поверхности равна 288 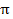 см2. Найдите радиус основания цилиндра.
см2. Найдите радиус основания цилиндра.
91. Диагональ правильной четырехугольной призмы составляет с боковой гранью угол 60°. Найдите объем призмы, если сторона основания 6 см.
92. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60°. Найти отношение объёмов конуса и шара.
93. Радиус шара равен R=5. Найдите площадь полной поверхности вписанного в шар куба.
94. Радиусы оснований усеченного конуса равны 4 см и 12 см, а образующая равна 17см. Найдите: а) высоту усеченного конуса; б) площадь осевого сечения.
95. В основании правильной четырехугольной призмы ABCDA1B1C1D1 лежит квадрат со стороной 8 см. Диагональ призмы AC1 образует с плоскостью основания ABCD угол 30°. Найдите высоту призмы и площадь полной поверхности.
Преподаватель Викторова Ю.В.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|