Тема урока: Системы линейных уравнений с двумя переменными

Тема урока: Системы линейных уравнений с двумя переменными

Цель урока: изучить понятие системы линейных уравнений с двумя переменными и выяснить, что является решением системы линейных уравнений с двумя переменными.

1. Прочитайте п. 42 учебника.

Система уравнений представляет собой два уравнения с двумя переменными, где требуется найти общие решения этих двух уравнений.

Систему уравнений принято записывать с помощью фигурной скобки.

Например,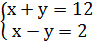

Решением системы линейных уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение в верное числовое равенство.

Например, решением системы 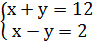является пара значений переменных х = 7, у = 5, так как оба равенства 7 + 5 = 12 и 7 – 5 = 2 верные!

Решение системы записывается как пара чисел в скобках: (7; 5), причём на первом месте в скобках пишут значение переменной х! а на втором – у!

Эту систему уравнений мы решили подбором.

Рассмотрим графический способ решения системы линейных уравнений с двумя переменными (т.е. используя графики уравнений).

Делаем записи в тетрадь!

Рассмотрим систему:

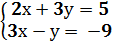
Построим в координатной плоскости графики уравнений системы:

1) 2x + 3y = 5.

Выразим из этого уравнения переменную yчерезx.

Для этого перенесём слагаемое2x в правую часть уравнения, изменив его знак: 3y = -2x +5.

Разделим обе части этого уравнения на 3 (каждое слагаемое равенства делим на 3): y = - x + .

ВСПОМНИТЕ, что такая формула задаёт линейную функцию, графиком которой служит ПРЯМАЯ! (п.16 стр.75 – 78).

Из геометрии нам известно, что для построения прямой достаточно двух точек! А значит, нам нужны любые два решения уравнения. Подберём их. Для этого - возьмите произвольное значение xи вычислитесоответствующееему значениеyпо формуле.

y = - x +

если x = 1, то y = - *1 + = - + 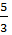= =1,получается пара (1; 1) – решение!

если x = 4, то y = - *4 + = - + 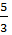= - = -1, получается пара (4; -1) – решение!

Отметим эти точки в координатной плоскости и проведём через них прямую.

2) .

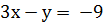Выразим из этого уравнения переменную yчерезx.

Для этого перенесём слагаемое3x в правую часть уравнения, изменив его знак: -y = -3x - 9.

Разделим обе части этого уравнения на -1 (каждое слагаемое равенства делим на (-1)): y = 3x + 9.

ВСПОМНИТЕ, что такая формула задаёт линейную функцию, графиком которой служит ПРЯМАЯ! (п.16 стр.75 – 78).

Из геометрии нам известно, что для построения прямой достаточно двух точек! А значит, нам нужны любые два решения уравнения. Подберём их, как делали до этого - взять произвольное значение xи вычислитьсоответствующееему значениеyпо формуле.

y = 3x + 9

если x = 0, то y = 3 * 0 + 9= 0 + 9 = 9, получается пара (0; 9) – решение!

если x = -2, то y = 3 * (-2) + 9 = -6 + 9 = 3, получается пара (-2; 3) – решение!

Отметим эти точки в координатной плоскости и проведём через них прямую.

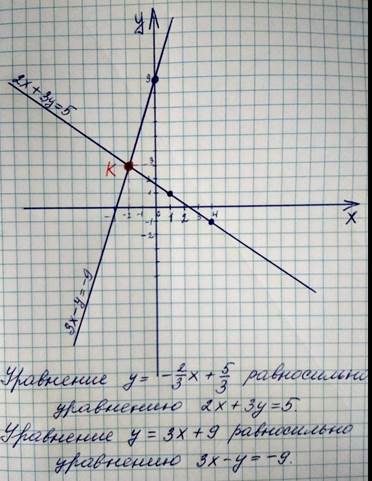
ВНИМАНИЕ!

Графики пересекаются в точке К(-2; 3). То есть это общая точка графиков, а значит пара (-2; 3) является решением и первого уравнения и второго.

ВЫВОД: пара (-2; 3) – единственное решение системы уравнений!

ОТВЕТ: (-2; 3).

2. В тетради выполните:

№ 1056 -используя определение решения системы уравнений, выясните какие пары чисел, являютсярешениями данных систем (нужно подставить вместо х и у числа, вспомните, что на первом месте в скобках идёт значение переменной х! а на втором – у!).

№ 1060 (а, г) –решить графически, используя образец выше (он записан у вас в тетрадь).