Тема урока: Решение систем уравнений методом подстановки

Тема урока: Решение систем уравнений методом подстановки

Цель урока: закрепить умения решать системы линейных уравнений с двумя переменными способом подстановки по алгоритму.

1.Прочитайте ещё раз алгоритм решения систем способом подстановки в п.43 учебника стр. 212.

2. Сделайте запись в тетрадь!

Рассмотрим следующую ситуацию:

№1069 (г)

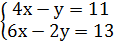
В этой системе, к сожалению, нет переменной, у которой коэффициент (множитель) равен 1. В первом уравнении у переменной у коэффициент равен - 1!

Из первого уравнения выразим у через х (сразу не получится):

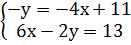
Умножим обе части первого уравнения на (-1):

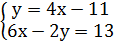
Подставим в другое (в данном случае, во второе) уравнение вместо у, полученное для него выражение из первого уравнения:

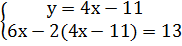
Решим полученное уравнение с одной переменной:

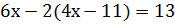
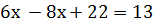
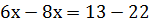
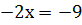
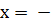9 : (-2)

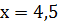
Найдём теперь значение другой переменной, то есть у! Для этого подставим в уравнение 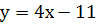вместо х число 4,5.

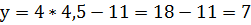
Ответ: (4,5; 7). На первом месте значение х, на втором – у.

3. В тетради выполните:

№ 1070 (а, б, в) –используйте данный ОБРАЗЕЦ и ОБРАЗЕЦ предыдущего урока, на первом шаге выражайте ту переменную, которую удобно. Это может быть и учерезх и х через у.

4. Выполните задания на «Фоксфорде».

Для этого в своём личном кабинете открыть программы обучения, выбрать предмет «алгебра», в левом столбике найти занятие №29 «Системы линейных уравнений с двумя переменными. Способ подстановки», нажать на кнопку «Перейти к задачам», там будет 5 задач.

Или по ссылке https://foxford.ru/courses/917/lessons/22274

Пользуйтесь черновиком!!!

Задача 1применить понятие «решение системы».Решением системы линейных уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение в верное числовое равенство.

Задача 2выразитьхчерезу.Образец смотрите выше. Суть одна, что у через х, что х через у.

Задача 3верно осуществить подстановку, в результате чего мы имеем уравнение с одной переменной.

Задача 4взять точку, принадлежащую графику и подставить её координаты в формулу.Когда получится верное равенство, тогда и будет соответствие графика и формулы.

Задача 5решить систему способом подстановки по алгоритму и в ответе указать сумму полученных значений (чисел) переменных a и b.

ОТМЕТКИ за эту работу будут выставлены в ЖУРНАЛ!!!