Контакты

Случайная статья

Касательная к графику функции. Алгоритм составления уравнения касательной к графику функции.. Решение.. Домашнее задание.

Касательная к графику функции

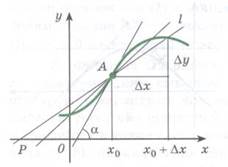С понятием касательной к графику функции мы уже знакомы. График дифференцируемой в точке х₀ функции 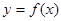вблизи х₀ практически не отличается от отрезка касательной, а значит, он близок к отрезку секущей l, проходящей через точк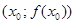и и 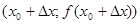. Любая из таких секущих проходит через точку 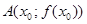графика.

Чтобы однозначно задать прямую, проходящую через данную точку А, достаточно указать её угловой коэффициент k. Угловой коэффициент 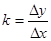секущей при 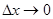стремится к числу .

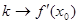Касательная есть предельное положение секущей при .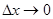

Касательная к графику дифференцируемой в точке х₀ функции 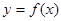- это прямая, проходящая через точку 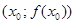и имеющая угловой коэффициент .

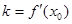Уравнение касательной к графику функции в заданной точке:

.

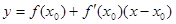Алгоритм составления уравнения касательной к графику функции.

1. Найти производную функции .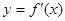

2. Найти значение производной в заданной точке х₀: .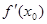

3. Найти значение функции в заданной точке х₀: .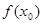

4. Подставить найденные значения в формулу .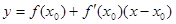

5. Упростить полученное выражение.

Пример.Найти уравнение касательной к графику функции 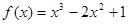в точке с абсциссой .

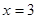Решение.

;

;

;

;

.

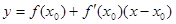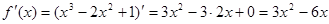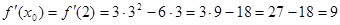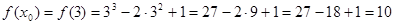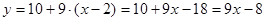Ответ: .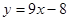

Домашнее задание.

№ 255. Напишите уравнение касательной к графику функции 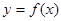в точке с абсциссой х₀.

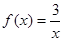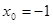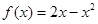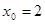а) , ; б) , ; в) , ;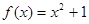

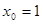г) , .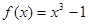

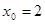© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.