Практическая работа № 4. Ход работы. вариант. Вариант II

Практическая работа № 4

Тема: «Координаты и вектора».

Цели:

· Расширить понятие вектор в прямоугольной системе координат в пространстве.

· Научиться раскладывать вектор по трём некомпланарным векторам (правило параллелепипеда) векторов.

Задачи:

повторить действия над векторами, заданными координатами, условие коллинеарности, перпендикулярности векторов, уравнение плоскости.

проанализировать и сделать вывод об актуальности координатного метода.

План выполнения практической работы

1. Выполнить самостоятельную работу.

2. Ответить на контрольные вопросы.

Ход работы

1. Задания самостоятельной работы:

1 вариант

1. Докажите, что четырехугольник ABCD является ромбом, если:

А (0; 2; 0), В(1; 0; 0), С (2; 0; 2), D (1; 2; 2).

2. Найти координаты вектора 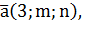коллинеарного вектору 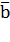(2;1;-2).

3. Найти координаты векторов 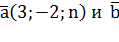(-1;1;4), если векторы перпендикулярны.

4. Найти угол между векторами: 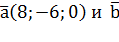(0;4;-3)

5. Составьте уравнение плоскости, проходящей через точку А(1;0;5), перпендикулярной вектору 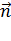(-2;-1;1)

Вариант II

1. Докажите, что четырехугольник ABCD является ромбом, если:

А (6; 7; 8), В (8; 2; 6), С (4; 3; 2), D (2; 8; 4);

2. Найти координаты вектора 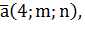коллинеарного вектору 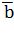(3;-1;2).

3. Найти координаты векторов (5;-1;6), если векторы перпендикулярны.

4. Найти угол между векторами: 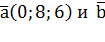(4;0; 3)

5. Составьте уравнение плоскости, проходящей через точку А(0;2;1), перпендикулярной вектору 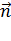(-1;-2;2)

2. Контрольные вопросы:

1. Длина вектора.

2. Определение скалярного произведения векторов.

3. Признак перпендикулярности векторов.

4. Признак коллинеарности векторов

5. Разложение вектора по трём некомпланарным векторам.

6. Уравнение плоскости.

7. Уравнение сферы.