Практическая работа № 10.. Тема: Решение задач о минимальном соединении в графе.. Вопросы для контроля

Практическая работа № 10.

Тема: Решение задач о минимальном соединении в графе.

Цель:научиться строить каркас графа с минимальным весом.

Вариант № 2

Ход работы:

Используя алгоритм Краскала построил каркас графов с минимальным весом (сравнил его с весом исходного графа).

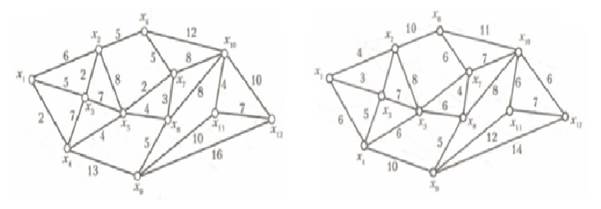
Исходные графы:

Граф 1.

Изначальный вес графа: 6+2+5+7+2+5+8+4+13+4+2+5+3+5+10+16+8+8+12+4+7+10=146.

Для решения задачи использую алгоритм Краскала:

1. Выписал все ребра из графа в список по возрастанию веса;

2. Выбрал в списке ребро e минимального веса и удалил из списка;

3. Если e не образует цикла с ребрами из списка ребер T, то добавить его в T;

4. Если список S не пуст, вернуться на шаг 2.

Рисунок 1 – каркас первого графа

вес каркаса графа:2+5+2+4+2+5+3+5+8+4+7=47.

Граф 2.

Изначальный вес графа: 4+3+5+6+7+6+8+10+10+6+4+6+5+12+14+7+6+6+11=136.

Для решения задачи использую алгоритм Краскала:

5. Выписал все ребра из графа в список по возрастанию веса;

6. Выбрал в списке ребро e минимального веса и удалил из списка;

7. Если e не образует цикла с ребрами из списка ребер T, то добавить его в T;

8. Если список S не пуст, вернуться на шаг 2.

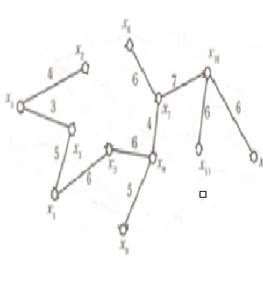
Рисунок 1 – каркас первого графа

вес каркаса графа:4+3+5+6+6+5+4+6+7+6+6=58.

Вопросы для контроля

1. Дать определение каркаса.

2. Привести пример использования алгоритма Краскала на практике.

Ответы на контрольные вопросы:

1. Каркас графа – это суграф графа, являющийся деревом.

2. Примером использования алгоритма Краскала на практике могут служить мосты в городе, для сокращения пути более длинные мосты можно закрыть

Вывод:научился строить каркас графа с минимальным весом.