
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
урок – зачёт: устная и письменная часть
20 мая
Урок геометрии, 10 класс
1 урок – зачёт: устная и письменная часть
От устной части зачёта освобождаются, те кто все задания и без ошибок сдавали в срок:
1. Березина Света
2. Васильева Таня
3. Коврова Дарина
4. Коротова Ольга
5. Иванова Ира
6. Бездетных Соня
7. Осипов Никита
Остальные сдают устную часть зачёта (вопросы к зачёту были выданы на прошлом уроке)
С 11:00 до 13:00 зачёт принимаю в Viber, WhatsApp.
Хочу вас увидеть и услышать. Завтра буду звонить.
 Задания для письменной части зачёта решают все.
Задания для письменной части зачёта решают все.
2 урок
Тема: «Повторение. Аксиомы стереометрии и их следствия».
Повторяем теорию
1. Аксиомы стереометрии и следствия из них
Учебник Стр. 4-7
Повторите и проверьте себя, вставив пропущенное.
1. Через любые ________, не лежащие на одной прямой, проходит плоскость, и притом __________.
2. Если ________ лежат в плоскости, то все точки прямой лежат в этой плоскости.
3. Если две плоскости имеют _______, то они имеют общую прямую, на которой лежат _________ этих плоскостей.
4. Через прямую и ________ проходит плоскость, и притом только одна.
5. Через две ______ прямые проходит плоскость, и притом только одна.
Решите задания теста
Часть 1
1. Верно, что…
1) любые три точки лежат в одной плоскости;
2) любые четыре точки не лежат в одной плоскости;
3) через любые три точки, не лежащие на одной прямой, проходит плоскость, и при том только одна.
2. AB и CD – диаметры окружности с центром O. Все точки окружности лежат в плоскости 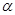 , если…
, если…
1) 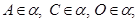
2) 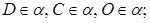
3) 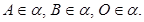
3. Верно ли, что прямая лежит в плоскости данного треугольника, если она…
1) пересекает две стороны треугольника;
2) проходит через одну из вершин треугольника;
3) содержит одну из сторон треугольника.
4. ABCDA1B1C1D1 – куб. Тогда плоскости (AB1C1) и (СDD1)…
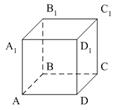
1) пересекаются;
2) не пересекаются;
3) совпадают.
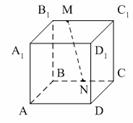 5. Прямая MN не пересекает плоскость…
5. Прямая MN не пересекает плоскость…
1) (АА1В1);
2) (ABC);
3) (AA1D1).
6. DABC – треугольная пирамида. Прямая BD непересекает прямую…
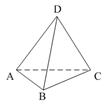
1) AC;
2) AD;
3) BC.
7. Сколько общих точек, не лежащих на одной прямой, не могут иметь две различные плоскости?
1) 1;
2) 2;
3) 3.
8. Даны две параллельные прямые a и b и точка M, не лежащая ни на одной из них. Точка M лежит в одной плоскости с прямыми a и b, если через точку M можно провести прямую, пересекающую…
1) хотя бы одну из данных прямых;
2) только одну из данных прямых;
3) две данные прямые.
9. Через три точки A, B и C можно провести единственную плоскость. Тогда точки…
1) не лежат на одной прямой;
2) лежат на одной прямой;
3) совпадают.
Часть 2
1. Точки A, B и С не лежат на одной прямой. Точка D не принадлежит плоскости (АВС). Через каждые три точки проведена плоскость. Тогда число различных плоскостей равно…
2. Плоскости 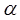 и
и 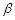 пересекаются по прямой m. Точка А лежит в плоскости
пересекаются по прямой m. Точка А лежит в плоскости 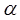 , точка В – в плоскости
, точка В – в плоскости 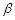 . Тогда прямая АВ лежит в плоскости
. Тогда прямая АВ лежит в плоскости 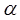 , если…
, если…
3. Проведены четыре плоскости. Каждые две из них пересекаются. Тогда наибольшее число прямых попарного пересечения плоскостей равно…
4. ABCD – параллелограмм. F 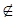 (ABC). Плоскости (ADF) и (OFC) пересекаются по прямой…
(ABC). Плоскости (ADF) и (OFC) пересекаются по прямой…

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|