
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
I. Дифференциальные уравнения 1-го порядка
I. Дифференциальные уравнения 1-го порядка
Обыкновенным дифференциальным уравнением первого порядка называется соотношение вида
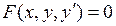 , (1)
, (1)
связывающее между собой независимую переменную, искомую функцию и ее производную.
Частным решением такого уравнения является дифференцируемая функция y = f (x), при подстановке в уравнение (1) обращающая его в тождество.
Множество всех решений уравнения (1) называется его общим решением, или общим интегралом и имеет вид
y = f (x, С), или F(x,y,C)=0 (2)
Любое частное решение получается из формулы (2) при некотором значении произвольной постоянной С, и наоборот, любое фиксированное значение С дает решение уравнения (1).
Задача нахождения частного решения уравнения (1), удовлетворяющего начальному условию y0 = f (x0), называется задачей Коши для уравнения первого порядка.
Рассмотрим некоторые виды дифференциальных уравнений первого порядка, для которых можно найти аналитическое решение.
1. Уравнения с разделяющимися переменными
Дифференциальное уравнение первого порядка вида
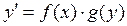 (3)
(3)
называется уравнением с разделяющимися переменными. Его можно привести к равенству 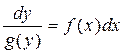 , откуда
, откуда  . Если существуют первообразные
. Если существуют первообразные 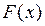 и
и 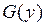 функций f (x) и
функций f (x) и  ,то общее решение урав-нения (3) имеет вид:
,то общее решение урав-нения (3) имеет вид: 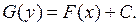
Пример 1. Найти общее решение уравнения 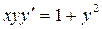 .
.
Решение. Разделим переменные:
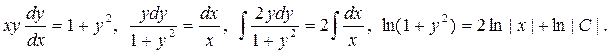
Обратите внимание на форму записи произвольной постоянной: если вид общего интеграла можно упростить потенцированием, удобно представить произвольную постоянную как логарифм другой произвольной постоянной. Тогда общий интеграл можно записать так: 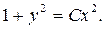
К уравнению с разделяющимися переменными можно привести и уравнение вида 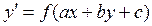 , (4)
, (4)
где a, b, c – постоянные. Для этого вводится новая функция z = ax + by + c. Поскольку 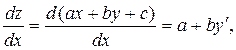
 и для z получаем уравнение с разделяющимися переменными:
и для z получаем уравнение с разделяющимися переменными: 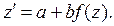
Пример 2.Найти частное решение уравнения 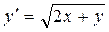 , удовлетворяю-щее условию у(4) = 1.
, удовлетворяю-щее условию у(4) = 1.
Решение. Пусть 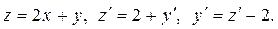 Решим уравнение для z:
Решим уравнение для z:
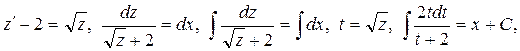
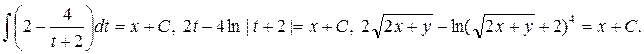 При х = 4, у = 1 получаем: 6 – 4 ln 5 = 4 + C, откуда С = 2 – 4 ln 5. Следовательно, частное решение имеет вид:
При х = 4, у = 1 получаем: 6 – 4 ln 5 = 4 + C, откуда С = 2 – 4 ln 5. Следовательно, частное решение имеет вид: 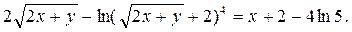
2. Линейные уравнения первого порядка
Уравнение вида 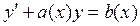 (5)
(5)
называется линейным неоднородным уравнением первого порядка, поскольку искомая функция и её производная в первой степени. Если b(x) ≡ 0, уравнение является однородным, причем это уравнение с разделяющимися переменными. На этом основан метод Лагранжа – метод вариации постоянной. Получив решение однородного уравнения 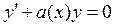 в виде y = f (x, C), считают, что решение уравнения (8) имеет такой же вид, но С = С (х) – не постоянная, а функция от х, вид которой можно определить, подставив y = f (x, C (х)) в уравнение (5).
в виде y = f (x, C), считают, что решение уравнения (8) имеет такой же вид, но С = С (х) – не постоянная, а функция от х, вид которой можно определить, подставив y = f (x, C (х)) в уравнение (5).
Пример 3.Найти общее решение уравнения 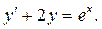
Решение.Сначала однородное уравнение:  . Теперь будем искать решение неоднородного уравнения в виде: у = С (х)∙е-2х.
. Теперь будем искать решение неоднородного уравнения в виде: у = С (х)∙е-2х.
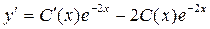 . Подставим y и y’ в исходное уравнение:
. Подставим y и y’ в исходное уравнение: 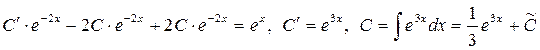 , где
, где 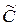 - произвольная постоянная. Следовательно, общее решение неоднородного уравнения:
- произвольная постоянная. Следовательно, общее решение неоднородного уравнения: 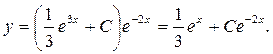
К линейному можно привести и уравнение вида
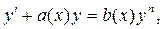 (6)
(6)
называемое уравнением Бернулли. Для этого вводится новая функция  , для которой
, для которой 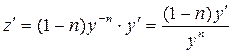 . Разделим обе части уравнения (6) на у п:
. Разделим обе части уравнения (6) на у п: 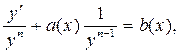 или
или  линейное уравнение для z.
линейное уравнение для z.
Пример 4. Найти общий интеграл уравнения 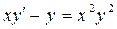 .Решение. Разделим обе части равенства на у2:
.Решение. Разделим обе части равенства на у2: 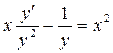 и сделаем замену:
и сделаем замену:  . Решим уравнение для z:
. Решим уравнение для z:  . Однородное уравнение:
. Однородное уравнение: 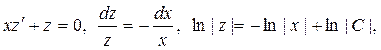
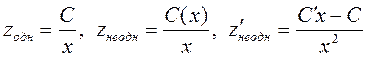 . Подставим полученные выра-жения в неоднородное уравнение:
. Подставим полученные выра-жения в неоднородное уравнение: 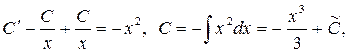
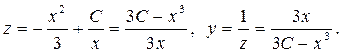
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|